在看過
之後的一點嘗試。
就我的認知,有限多的 singular points 無法破壞這裡的拓墣特性,所以討論非碎形曲線的時候,頂多討論能夠減少內接矩形到什麼程度。所以我真正有興趣的是局部構成沒有內接矩形時,如何重複這個構成還是保持特性。
然而一次跨出這步太超出我目前所知了,所以只能先考慮相關的變形問題:首先,開放的曲線可能沒有內接矩形,比如下圖由兩個有界直線構成(箭頭表示無限延伸方向)
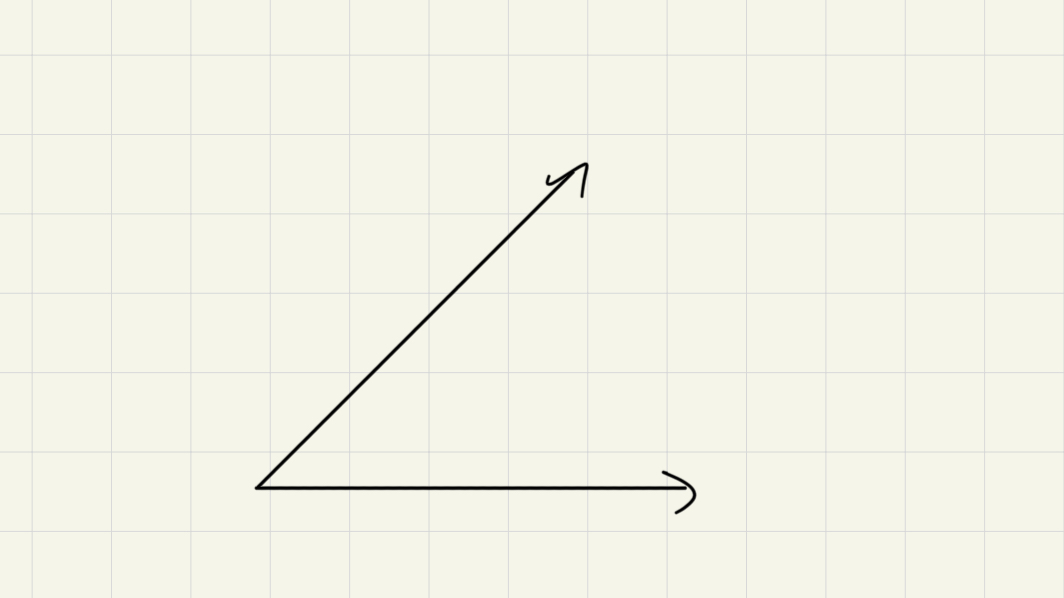
- 如果選擇了頂點與其中一邊的點,那麼法向只能再跟此圖交於一點,無法構成矩形。另一邊因為對稱性所以一樣。
- 如果選擇一邊的兩點,那法向接觸到另一邊的長度不同,自然也不是矩形。
- 如果一邊各自選一點,因為這條邊往任意一邊移動都會改變長度,也沒辦法構成矩形。
但這張圖如果稍作修改,比如加一個直線拉回來變成三角形,就會再次有內接矩形。
另一種值得考慮的基本構造是圓,因為可以說圓的內接矩形有無限多個,但也可以說某種程度上只有一個內接矩形。所以如果考慮取半圓形,另一半則是想辦法破壞對稱性,比如我考慮過的其中一種形狀是

想法就是一直取一半直徑的半圓去填右半部。這個旋轉一下就可以弄成方程組,所以要驗證這個圖形可以嘗試看看方程組中出現矩形要怎麼驗證。