This blog majorly writes about computer science and mathematics, also is my personal public notes. Feel free to point out any good reference of topic you view on the site, I will add them into reference if proper.
You can use Ctrl + K (or Meta + K on MacOS) to toggle search bar.
Posts [posts]
Posts [posts]
RSS in emacs:elfeed [EHWW]
RSS in emacs:elfeed [EHWW]
I've been trying some Emacs packages, including elfeed and meow, but the latter is not the topic of this post. I will briefly introduce elfeed package.
I use straight.el to install packages:
(use-package elfeed
:custom
(elfeed-feeds
'("https://dannypsnl.srht.site/rss.xml")))
elfeed-feeds is where you configure the feeds. Here I use my personal site as an example. Use M-x elfeed to open a buffer of elfeed. In this buffer, pressing G will fetch and refresh the feeds. Once articles are listed, pressing Enter will open the selected one. In reading mode, n and p move to older and newer articles, respectively.
Pattern Unification 演算法理論部分 [F6C1]
Pattern Unification 演算法理論部分 [F6C1]
在這篇文章裡面我想要探討 Elaboration Zoo 裡面的 pattern unification 演算法怎麼算出來的,以及在什麼時候成立。主要是了解我們怎麼導出等式:
超越 Elaboration zoo 中的合一演算法與隱式參數 僅是直覺的推理。在 Display map category 我們已經了解到,contexts 跟 substitutions 構成了一個範疇,而我們想要知道的是 epimorphism 的定義,所以 Kovacs 的第一步是把 epimorphism 定義改寫成更適合這個案例的定義
Definition. Epimorphism [local-0]
Definition. Epimorphism [local-0]
我們說 是 epimorphism iff
這也導出了 term 的事實:
我們關心一個 substitutions 中的子集:renamings
Definition. Renamings [local-1]
Definition. Renamings [local-1]
一個 substitution 如果純粹由變數構成,那麼它是 renaming,記成
而且 Renaming 有以下特性
- 如果只用到 中的變數至多一次,那麼 是 epimorphism
- 如果只用到 中的變數至少一次,那麼 是 monomorphism
- 如果只用到 中的變數剛好一次,那麼 是 isomorphism(context 的 permutation)
Definition. Embeddings [local-2]
Definition. Embeddings [local-2]
Renamings 還有一個子集叫 Embeddings,是 為 捨棄 0 到多個變數後組成的 context。
- 每個 embedding 都是 epimorphism
- embedding 一定是 identity
Renaming 總是能被分解為(這個動作叫 strengthening,可以延伸到 type/term 的 substitution 上)
其中 是一個 monomorphism,而 是一個 embedding
Pattern unification 問題是,在某個 context 下有等式
其中
所謂的 pattern conditions 是以下 3 個條件
- 是一個 epimorphism 跟 renaming,可以分解成
- 這個 meta variable 在 中不是自由變數
是 epimorphism 意味著 也是 epimorphism,因此 是 isomorphism,具有 inverse 。從初始問題出發
分解 得到
替換 得到
embedding 是 epimorphism
套上
inverse 對消
這促使我們定義 ,然後就只需要檢查 不是解的自由變量就可以了,原因參考 Elaboration with first-class implicit function types 的細節。直覺一點來說,本來的假定條件會導出 不是自由的,如果檢查卻發現它是自由的,就表示假定條件不成立。
最後
- 判斷 Renaming 是不是 epimorphism
- 分解 Renaming
- type/term 的 strengthening(如果 type theory 是 normalizing)
這三個演算法都是可判定的,因此 pattern unification 這個演算法是可判定的。而且由於分解唯一,解也是唯一的。
安裝 Guix [B4OI]
安裝 Guix [B4OI]
下載之後按照系統安裝文件描述的方式把 iso 燒錄到 USB or DVD,插入電腦開始安裝。基本上現在的引導介面已經跟 ubuntu 之類的老牌 distribution 相當了,只要按照螢幕上說的逐步回答就能設定完成。
它的 root 跟一般帳號是明確分開的,密碼也不同,在設定完 root 密碼之後會要求建立至少一個一般帳號。partition 分成兩種,按照需求選擇就好。最後選介面時有很多選擇,Gnome、KDE、Sway 都有,這個也是習慣用什麼就選什麼就行了。這之後就會開始安裝,跑完之後重開機(boot 管理要記得切換到安裝好的系統才不會又跑進 installer)。
到這裡就可以看 https://guix.gnu.org/manual/1.5.0/en/html_node/Getting-Started-with-the-System.html 文件開始編輯 /etc/config.scm 了。
2026 - Week 5 [2026-W5]
2026 - Week 5 [2026-W5]
Racket 中的 concurrent programming [local-0]
Racket 中的 concurrent programming [local-0]
想到就測試 rakka 跟 Racket coroutine thread 結果 native 還比較快XD,所以我就把 genserver 做成 Racket thread 封裝了 https://codeberg.org/dannypsnl/erl。至於為什麼 coroutine thread 這麼快,我猜可能 CS 之後有很大改善,我之前沒有注意到這點
Racket language server [local-2]
Racket language server [local-2]
racket-langserver 這個 PR 的目的是改善目前一團糟的測試體驗。現在的方式是啟動 subprocess 然後跟它的 stdio 互動,一來這意味著大量的系統資源需求,二來耦合這麼重就很難設計可以遠端連線的 server。所以第一步需要清理現在的設計,引入間接層讓測試只需要跟這個抽象部分互動就好
racket-llvm [local-3]
racket-llvm [local-3]
改善一下 racket-llvm 的文件,修復案例
2026 - Week 4 [2026-W4]
2026 - Week 4 [2026-W4]
試著寫了 JIT 框架,研究了 JIT: Write XOR Execute policy 怎麼實現。目前放在 https://github.com/dannypsnl/still-compiling/tree/develop/dynasm 中,目前還遠遠不成熟,可能做幾個 example 之後才會考慮釋出
Rakka 使用初體驗 [GMYW]
Rakka 使用初體驗 [GMYW]
最近發現 racket 生態系裡面出現一個 Rakka 程式庫,它似乎把 Erlang 大部分一階抽象都做出來了,這是我個人想像很久的寫法,所以我當然很有興趣去嘗試。我的第一個實驗是針對的 sauron 內部程式庫 collector 進行重構。collector 原本就是模仿 Erlang 的訊息傳遞方式來抽象,使用 rakka 之後,我直接把這些抽象邏輯寫成 GenServer 的形式。結果發現效果非常不錯
- 程式碼數量減少:collector 的程式碼量變成原來的大約三分之二。
- 維護性提升:整體結構變得更好維護。
所以之後遇到類似的需求,我就會考慮使用 rakka 處理,我就不用再寫處理訊息傳遞風格的樣板式重複程式碼了。而且它還實現了 EPMD protocol,可以跟其他 node 互動。
Display map category 捕捉了類型論的什麼面向? [tt-BBGG]
Display map category 捕捉了類型論的什麼面向? [tt-BBGG]
要理解 Display map category 的定義(參考 Categorical Logic and Type Theory, Definition 10.4.1),我們需要理解它的動機跟捕捉問題的方式,因此我們要觀察一個個相繼式(我假設讀者已經熟練相繼式定義的類型論),並用範疇論(category theory)的語言重述。
在用相繼式描述類型論時,公式
表示 可派生出類型 。對於所有 可派生的類型,我們用 表示,所以我們也會用 來表示上面的相繼式。Display map category 捕捉的第一件事就是 contexts 構成一個 category,我們用 記號表示這個範疇,並且我們要求 有 terminal object ,用來表示空的 context。
context 的構造方式只有兩種: 是一個 context;context 加入一個類型 得到的 還是 context。
因此 也常被稱為 telescope
在相繼式中如果我們寫
我們的意思是 ,對於每一個 ,都能找到 ,我們稱「 實現了 」。
但上面那樣寫有問題,因為 沒有憑依,因此正確的通用寫法是記錄成
這表示 參考 中的變數,並實現了 ,這叫做一個替換。
對 type 套用替換 [local-0]
對 type 套用替換 [local-0]
如果我們同時有 跟 ,那我們可以對 進行替換得到:
換句話說,我們用 完成了一個逆變,記成 。
對 term 套用替換 [local-1]
對 term 套用替換 [local-1]
用相繼式時
表示 在 中有類型 ,當然,這裡隱含的前提是 。
而替換同樣可以在 term 上作用:
對替換套用替換 [local-2]
對替換套用替換 [local-2]
但我們也知道替換 也能看成一個 term,所以同樣可以對它套用替換!
這說明了替換可以結合!我們經常記成 。
而很明顯的,對於所有 有一個「引用變數 來實現 的不變替換 」,所以我們想把每個替換 視為 中的 morphism 。這裡需要證明幾件事
- 對於給定的 ,可能的 的 collection 是一個集合。由於所有替換都涉及對 的引用(或是有限多的類型生成規則)並做出一個有限構造,所以可以用歸納的方式比較,這讓證明是唯一的,因此這些替換是 set
- 對 來說有 。根據定義就知道了
- 替換要有 associative 。這個不好證明,就我所知都是對規則進行 induction 得到(參考 Substitution Without Copy and Paste 的 §4.3)
現在我們要進入 Display map 的部分
Definition. Display map [local-3]
Definition. Display map [local-3]
對於 與 ,我們有 ,這叫做 display map。提醒一下這個相繼式是
考慮逆變,就得到
唯一確定了一個類型,也就是說現在每個 type 都被一個某一些替換代表了。這也可以說其實我們在看 這些 morphisms。
term 的表示 [local-4]
term 的表示 [local-4]
同理可以放到 term 上,對於
可以視為
也就是說每一個 term 都可以看成替換
到這裡我們發現,這個模型很好的捕捉了 syntactic categorical 的觀點,把類型論的句法特性都保留了下來。前面說過每個替換都有逆變,現在我們要證明逆變是一個 functor:
Proposition. 逆變是 functor [local-6]
Proposition. 逆變是 functor [local-6]
對於任何 ,我們把逆變看成 slice category 的函數 ,要檢查這是否是 functor,我們想要證明兩件事:保留 identity 且保留 composition。
Proof. [local-5]
Proof. [local-5]
套上 display maps 的規範,知道逆變會產出一個 pullback:
這直接證明了 ,所以 ,表示 保留了 identity。
要證明 composition,可以用 pullbacks 的結合知道如果 跟 的頂點 up to isomorphism 是同一個,因此這兩個 morphism 是一樣的,證明了也保留 composition。因此每個替換誘導出的逆變都是 functor。 □
既然 是個 functor,那在 display map category 裡,我們可以用 的 right adjoint 表示 product,而且加上 Beck-Chevalley 條件:存在一個 natural isomorphism,讓我們可以把 product 用替換推來推去而不會變成不同的東西。
weak sum 同理,只是變成 的 left adjoint,同樣要有 Beck-Chevalley 條件保證 coproduct 可以被推來推去而不遺失。strong sum 則是把條件強化到 display maps 組合一定是 display map,這蘊含 weak sum 條件。
我們前面完全沒有提到 這種形式,而確實這是 display map categorical 方法的額外條件:weak equality 用 diagonal 的 left adjoint 表示,還是用 Beck-Chevalley 條件避免遺失。strong equality 規定 diagonal 是 display map,蘊含 weak equality。
對細節有興趣的讀者可以看 Paige Randall North 的 slide:Homotopical models of type theory
現在我們看到,display map category 除了捕捉 type theory 的 syntactic 特性,還可以用直觀的範疇論語言表述 type theory 的數種特徵,成功的讓我們用範疇論的觀點來檢視類型論。
現代 - 商業、科技與政治交織的空間 [U5YI]
現代 - 商業、科技與政治交織的空間 [U5YI]
讓我們先從 LLM 開始談起,我認為 Context Widows 的觀點很適合開始理解問題在哪裡。問題不在 LLM 或是廣泛的 AI 領域有用或是沒用,正如 Context Widows 一文自己所說跟我從其他地方看到的,正面的產出確實存在,像是
- 蛋白質折疊
- 材料科學
- 用壓縮映射模擬星系演變
而可質疑的問題也一直存在:幻覺、缺乏理解。更不用說直接的負面影響
- 氣候
- 佔用能源(包含在天災時電網供電給計算中心而不是醫院)
- 剽竊創意
Context Widows 真正要談的是,比起問 LLM 有沒有用,更恰當的問題是:LLM 能否有效地融入科學知識的創造、驗證和傳播過程中?
LLM 能否有效地融入科學知識的創造、驗證和傳播過程中? [local-0]
LLM 能否有效地融入科學知識的創造、驗證和傳播過程中? [local-0]
由於一項技術的潛在用途並非其實際用途,而實際用途又取決於採用該技術的機構、機構試圖解決的問題以及機構用作衡量成功的既有指標。所以 Context Widows 認為探討 LLM 與科學的關係,等若詢問 LLM 出現之前,科學界已經運作著怎樣的體系?
我們知道當代科學界的主導是引用體系,隨著時間發展,引用體系已經改變它本要量測的對象;科學家會調整自己的行為以最佳化指標。Context Widows 也駁斥用古德哈特定律「當一個指標成為目標時,它就不再是一個好的指標」來解釋這件事,因為古德哈特定律只認為指標是問題,但 Context Widows 一文認為有問題的是需要指標才能運作的組織形式。
在這個背景下,LLM 雖然有其他的功用,卻只會加速學術界的固有邏輯:更多的發表。引用文中的話來說
LLM 並非經濟學家(一群熱衷於用貶低維度的方式來消除意義的人)所稱的科學激勵「結構」的創造者。相反,這項技術恰好出現在這樣的背景下,提供了一種更快的方式來生產系統所獎勵的成果。
而很明顯的,這不局限於學術界中,搜尋引擎的誕生改變了網路,SEO 變成很多網站在意的事,從而產生了內容農場這樣製造垃圾的存在。
到這裡我們先總結 Context Widows 的結論:
LLM 並非科學出版功能失調的始作俑者;它們繼承了這種功能失調,加劇並使其運行得更快。就像一種通常無害的病原體在免疫功能低下的患者體內肆虐一樣,它們指出了問題所在,但如果將它們視為問題的全部,那就大錯特錯了。人們或許會希望這種加速發展能加劇矛盾,讓系統如此迅速地產生大量劣質內容,最終讓問題變得無可辯駁。但是,正如我們現在應該都明白的那樣,系統可以無限期地處於功能失調狀態,而荒謬本身並不會自我糾正。這種加速發展究竟會導致崩潰、適應,還是只是延續現狀,並非技術本身的問題,也無法透過關於技術能力的爭論來解答。答案將由運行這個計畫六十年的機構來解答。
於是現在我們可以更進一步的詢問:LLM 能否有效的融入商業的創新、運作和責任之中?
LLM 能否有效的融入商業的創新、運作和責任之中? [local-1]
LLM 能否有效的融入商業的創新、運作和責任之中? [local-1]
同樣的,這使得我們去問:LLM 出現之前,商業運作著怎樣的體系?
在經濟學追尋公司的意義時,Milton Friedman 在 1970 年提出 The Social Responsibility of Business Is to Increase Its Profits,直譯大概就是「企業的社會責任是增加利潤」,這是當代企業的主流追求與試圖實踐的理想。這有什麼樣的後果?
Paul 有兩篇相關的 thread,很清晰的闡述了當代的企業環境
- https://hachyderm.io/@inthehands/113603661215753448
- https://hachyderm.io/@inthehands/115793003693199462
儘管我們大多數人都生活在現代企業地獄般的環境中,仍然無法理解大企業的運營究竟有多麼嚴重的破碎,以及它們在多大程度上依靠虛假、欺騙和胡言亂語來運作。
所以,為什麼公司部署 LLM 呢?Paul 讓我們從底線來看:XX 公司的新 AI 客服描述不存在的功能,或是叫人們去吃釘子或膠水。會怎樣嗎?嗯反正他們以前那些不幸的、缺乏訓練的、工資微薄、像泥土一樣被對待的客服人員(過去負責處理所有的客戶支援),實際上也沒有幫助人們。由於 XX 公司對吞吐量的要求如此之高,並且對問題關閉的激勵如此之大,以至於他們的客服人員帶領人們白費力氣,罵人或放棄回應。LLM 不會罵人,不會放棄回應,吞吐量極高。它在帶領人們白費力氣上「遠遠」比人類更有效率,而且有時候僅僅靠運氣,它實際上是對的!
從底線來看,部署 LLM 其實沒有那麼糟糕!所以現況其實是
商業活動為世界提供的實際價值如此之少,以至於用快速、自動化的廢話取代緩慢的人類廢話似乎是一場勝利。
所以對於採不採用 LLM,我們可以問的問題是:如果它是錯誤的,那麼重要嗎?Paul 以特斯拉為案例:特斯拉正在銷售這些「顯然」還沒有準備好迎接黃金時段的自毀汽車,它們會用事故後打不開的車門將人們困在裡面,然後將他們活活燒死。而且他們仍然在銷售大量這些東西。如果對他們來說這樣都無關緊要,那有多少虛假和危險的商業環境是可以被他們接受的?
LLM 是假的?又怎樣呢?商業也是如此。
更具體的說,LLM 會對管理層帶來什麼影響?對糟糕的組織領導人來說,讓擁有專業知識的下屬不去檢查他們的想法基本上就是成癮性藥物。那 LLM 豈不是就是不會拒絕他們任何「高妙」想法的完美下屬?這是一種強大的心理力量,促使我們快速地往採用 LLM 滑動,無關乎這是否有用。
所以同樣的,LLM 表現出的,是對既有商業實踐的加劇與加速,放大既有的功能失調。在 LLM 以前同樣有 08 年的次貸風暴,遵循一樣的系統運行規則而致。
監控資本主義提出現代商業的核心邏輯是:資本的來源是販售預測;最容易被預測的人群,是被監控甚或控制的人群。因此獲利的動力會驅動大規模的監視與控制。
按吳修銘的話來說,即使是 Google 最大的反對者也很難說監控資本主義談的是 Google 的主要目的。但這可以被視為一個特別黑暗的隱喻,指向現代商業實踐的最糟結果。而現實中最接近的,是中俄等專制政權已經學會怎麼用現代技術影響他國的政治。
- 《讀賣新聞》報導台灣政府正高度警戒中國透過操縱輿論介入選舉
- 法國國際廣播電台報導歐洲如何應對俄羅斯的政治宣傳和軍事威脅?
再次的,LLM 提供了加劇破壞社會討論的一種方式,即用無限量的劣質資訊破壞言論場域,但這是因為網路早已逐漸侵蝕了公眾對談的能力。參見 Are we too connected to social media? An explanatory research the problematic social media use in self-esteem, phubbing and procrastinating behaviour。
LLM 能否有效的融入人的成長、交流與生活中? [local-2]
LLM 能否有效的融入人的成長、交流與生活中? [local-2]
LLM 能否有效的融入人的成長、交流與生活中?這當然是一個複雜的問題:LLM 出現之前,現代人類是怎麼成長、交流與生活的?
- 現代的主流成長方式,是未成年人類放到學校;而成年人上網看一些什麼如何投資、如何成長的東西,比如人們會看教你如何閱讀的影片,但不會真的去閱讀。對了,老闆想要成長 — 我們就讓老闆「看見」成長。
- 現代的主流社交方式,是在稱之為社群媒體或是社交平台(像是 threads、IG、FB)的地方對幽谷大喊,由演算法控制人們看到什麼(你很好奇為什麼 meta 好像持有前述的所有平台?這是很好的好奇)
- 現代的主流過活方式,是必須上 8 小時以上的班,換取大概能過活的薪水,在剩餘的時間想辦法娛樂自己,我們勉強稱之為生活
LLM 會怎麼影響,要看 LLM 有哪些具體的施展位置。
在學校逐漸提高效率要求的情況下,你要怎麼譴責老師:用 LLM 生成題目、改答案、規劃教學?
在課業繁重的情況下,學生要怎麼不用 LLM 生成作業?尤其是成績如果能因此提高,而系統獎勵成績時?
人們要怎麼分辨出 LLM 生成的留言然後避免被影響?
人們要怎麼在生活壓力越來越大時不對 LLM 宣洩情感?至少它不會罵我們
人們要怎麼在不因為能對 LLM 下令而被權力損傷?
oh, I just realized: does this mean that AI gives everyone the chance of the brain damage humans get from too much power too long?
要怎麼在搜尋引擎預設就提供 LLM 合成答案時去搜尋原始文章,確認內容?
要怎麼在繁重的工作壓力下保持生活?
上述的問題,有些出自商業邏輯,有些跟我們的社會運作有關,有些是因為人類的生理能力。再次的,LLM 加劇我們的問題,但不是唯一的原因。要讓 LLM 技術不對人類造成危害,就要在這些具體的案例中找出我們的解答。
注意到,這篇文章的目的不是號稱 LLM 全然的不好,或是商業多麽的灰暗;即使是最荒謬的公司中都有很多好人試著改善問題;學術界就算深受引用指標影響,也依然有大量有用的研究出產。最糟糕的莫過於直接跳過具體案例的討論,做出這個世界已經完全沒有救的結論。
這篇文章的目的是,從我有限的觀察與閱讀中,指出具體的商業、科技與政治問題,並且試著改善它們。如果問萬事揭曉:打破文明演進的神話,開啟自由曙光的全新人類史最重要的意義是什麼,我會說是 Graeber 指出人類具有想像並構造自己的政治的能力,遠超過當代人對自己的想像。或許我們可以試著打造一個世界,減少指標的需要、降低對效率的要求、更關心你我周遭的人、更注重環境對我們說的話,這不是什麼烏托邦,衝突不會簡單的消失,但我們需要真的開始對話跟行動,這一切才有出路。
2025 年 [2025]
2025 年 [2025]
今年開源的一點貢獻
- 自己弄了個網站生成工具 tr
- 弄懂怎麼生成 induction principle
- 參與了一點 Yoxem 的 SICP 台語翻譯計畫
- agda-mode-vscode 提示 unicode 符號輸入方式
- 讓 magic-racket 可以開啟 macro 展開過程的互動 GUI 用來除錯
- racket-langserver 的維護,今年底突然獲得管理權限xd
然後我下定決心研究了 epub 檔案格式,讓我更清楚可以對這些書籍檔案做什麼xd。因為年初我自己立的目標是看懂 mirror symmetry,數學我今年大致上學了
mirror symmetry 的表示論前提
- -linear category
- cochain complex: 一系列 vector spaces (或是 graded vector spaces)加上一個 degree 1 的 linear map
- cohomology: 按組成取 也是一個 graded vector space,這就是 cohomology 了
- algebra 與 category
- Twisted complex
另外從微分幾何的方向看了一點物理學的對稱性怎麼用來描述費米跟玻色場。不過這些內容的意義為何?要解決什麼問題?似乎又回到需要代數幾何的基礎上,因此這裡得先放著了。
- preadditive/abelian category
- 一點 commutative algebra
- 一點 Lie algebra
今年末尾嘗試寫了各種 agda,讀了點 HoTT 中的 higher inductive types 跟 synthetic geometry,結合上面需要代數幾何的部分,讓我想往 synthetic geometry 的方向試試,或許先看看幾篇相關論文的未來研究方向跟未解問題?
閱讀 [local-0]
閱讀 [local-0]
- 監控資本主義時代 上卷: 基礎與演進/ 下卷: 機器控制力量:除了這本書本身指出的極端情況,還有數個對現況的相關看法應該一起吸收,我應該會再寫一篇文章寫這方面的感想
- 萬事揭曉:打破文明演進的神話,開啟自由曙光的全新人類史:作者認為大眾對人類發展史的看法深受盧梭與霍布斯的遺緒影響,而考古與人類學證據足以駁斥這些觀點
- 慈禧: 開啟現代中國的皇太后:這是在 mastodon 上看別人看很有趣就去買的書,作者盡力基於歷史證據描繪了一個與學生時代課本所述完全不同的慈禧
- 不實在的現實:以演化為基本的公理的話,我們會推導出什麼樣的世界觀?我覺得有關聯、也很有啟發性的是訪談 Michael Levin 討論的事情
- 勤儉魔法師的中古英格蘭生存指南、侑美與夢魘繪師、翠海的雀絲、日煉者:嚴格來說日煉者我只看了一半,不過應該很快就能看完xd
- 裸顏(Till we have faces):這本小說的劇情很明顯不能按照字面意思去讀,賽姬跟歐若要解釋成一個人或是兩個人都可以,而「神」的意義也明顯有多重意義,每次閱讀應該都會投射自己的人生感想進去吧xd
技術性的東西其實比較好寫,做到哪裡就說什麼。今年六月的時候去台中找朋友,雖然大罷免沒有成功,但很高興台灣有這麼一群人,民主的重點從來都不是政黨,而是表達意願、付諸行動的公民。台灣的未來、人類的未來,目前看起來都比較灰暗,我不會指望明年就會有什麼差別,但願我們能學會不輕視人文、理解不同的文化、解決共同的難題。
Rhombus 用標記運算自動排序資料 [programming-0005]
Rhombus 用標記運算自動排序資料 [programming-0005]
最近在研究 Shrubbery Notation 怎麼實現 operator 優先序的過程中(卡關中),又發現 Rhombus 的 meta 功能中有不少有趣的東西,比如現在要介紹的功能:標記運算。要使用這個功能,必須在開頭宣告
#lang rhombus/and_meta
或是
#lang rhombus/static/and_meta
語言。接著定義
annot.macro 'AscendingIntList': 'converting(fun (ints :: List.of(Int)) :: List: ints.sort())'
這會在我們寫下
[3, 1, 2] :: AscendingIntList
時,得到 [1, 2, 3] 而不是 [3, 1, 2],因為這個標記會自動進行排序運算!
具體的 simplicial set: Torus [math-001J]
具體的 simplicial set: Torus [math-001J]
simplex 要怎麼跟幾何扯上關係?這是因為 up to homotopy,我們可以把幾何形狀變形成用一群三角形(確切的來說是一些 simplex)表示的形狀。這裡要講的案例 Torus 是一個二維度的幾何曲面,一般定義成 並畫成
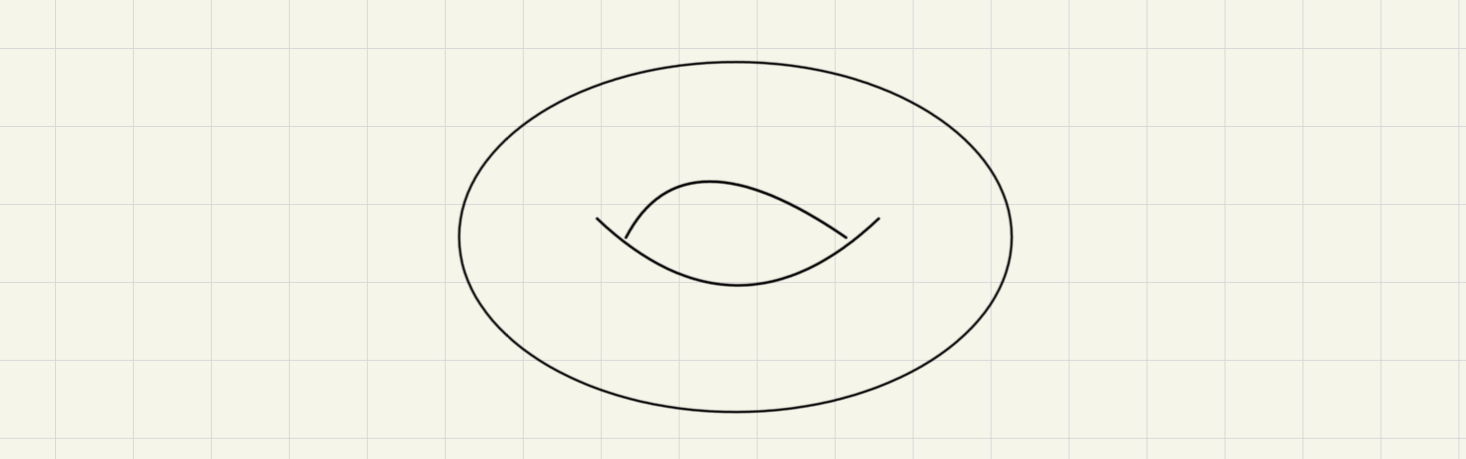
要怎麼三角化呢?通常會簡化成
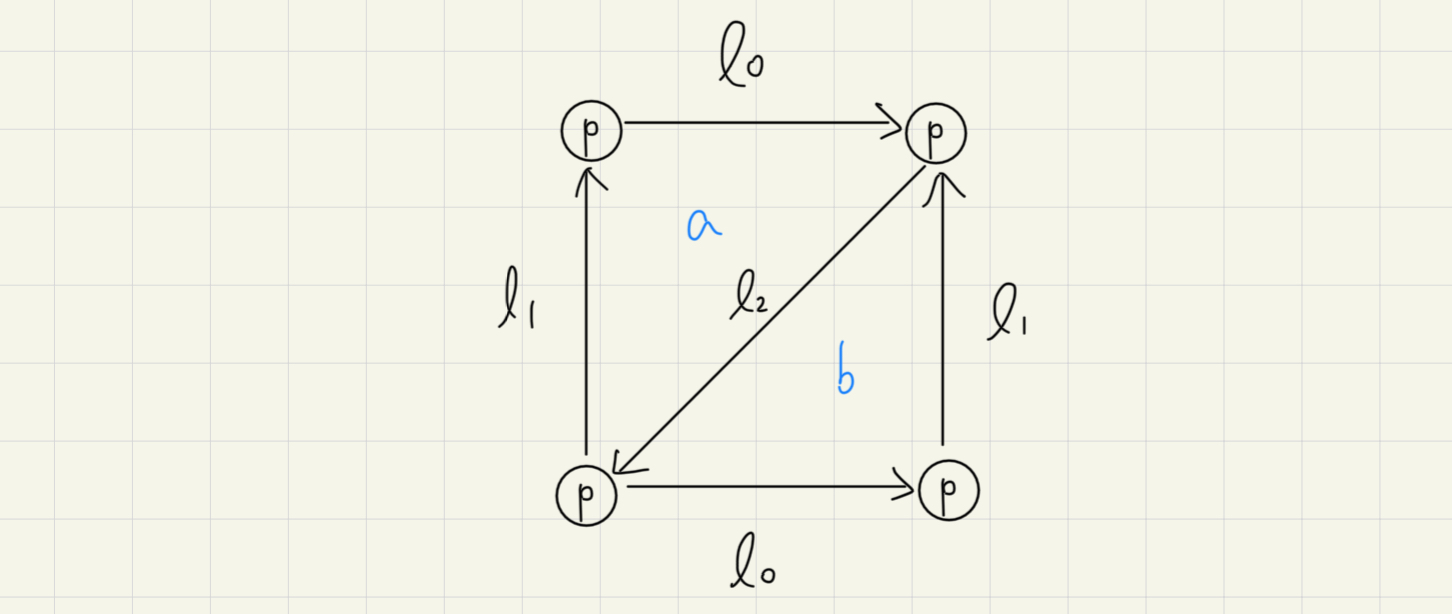
這怎麼變成幾何形狀的?注意到標為同一個名稱的那些線,那表示那其實是同一條線。這需要定義一個 simplicial set (Hint: 根據定義是個 contravariant functor),其資訊如下:
視為其幾何實現(geometrical realization):
每個 topological space 都導出一個 simplicial set ,每個 -simplex 都是 到 的連續函數:
每個連續函數,都給出了連續變形的過程;第二部分則是取 restriction,保持邊界關係。我下面展示如何逐漸變形來解釋其意義:
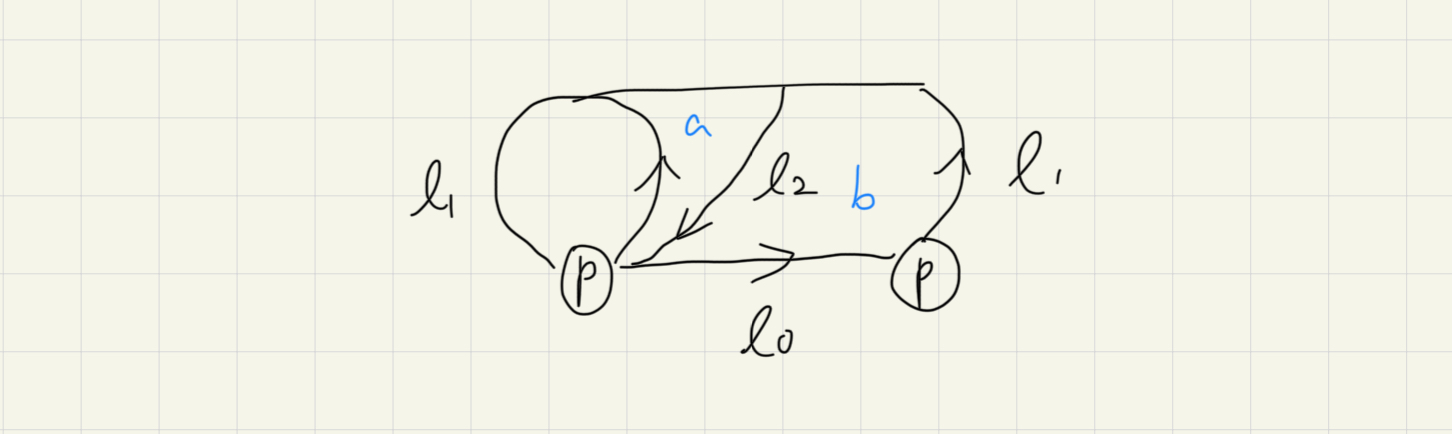
接著把管子對接
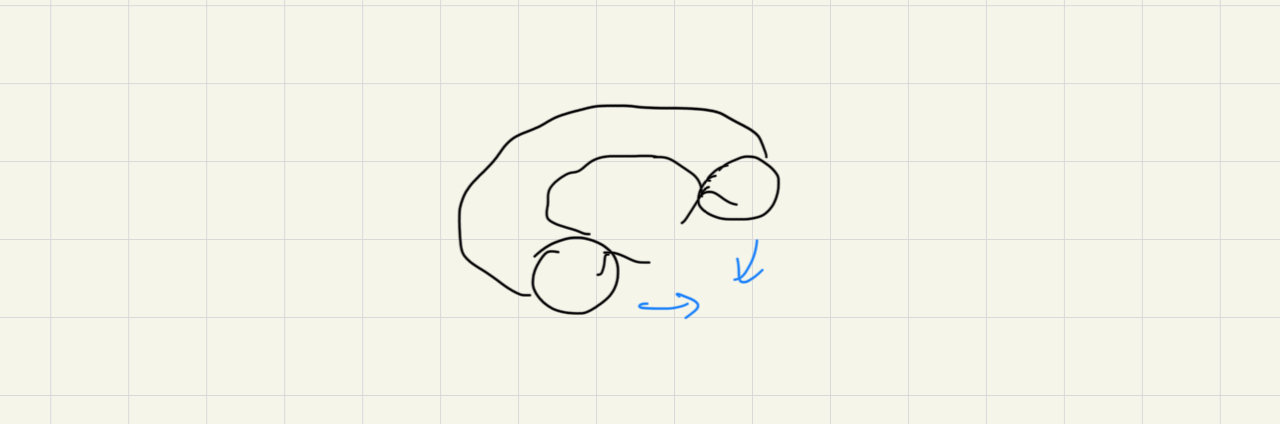
這確實是 Torus 的模型。
Integrating Mathlive into editor.js and Thoughts on Note-Taking Systems [programming-0004]
Integrating Mathlive into editor.js and Thoughts on Note-Taking Systems [programming-0004]
editor.js is a free, block-style (composable) editor with universal JSON output. Hence, it's a nice foundation for building your own rich-text editor.
mathlive is a math editor for the Web, specifically a custom HTML element with functionality to edit math formulas:
<math-field> x^2 + y^2 = 1 </math-field>
editor.js is extensible. Specifically, when creating an editor.js instance, one can provide customized tools to it:
new EditorJS({
holder: editorContainer,
autofocus: true,
tools: {
header: Header,
underline: Underline,
strikethrough: Strikethrough,
list: List,
}
})
These tools are node packages you need to install. As you can see, editor.js is highly modular, which is good because I'm going to add a new tool here. I'm going to show how to build a mathlive tool called Formula for editor.js (and perhaps I'll extract it as a package in the future).
A custom tool requires some basic setup, which is common to all tools
class Formula {
static get toolbox() {
return {
title: "Formula",
icon: "...",
};
}
constructor({ data }) {
this.data = data;
this.wrapper = undefined;
}
}
- A tool is a JS class
- In
toolboxwe can configure the title to show and the icon (which is a string of svg syntax) - We need to restore from data when constructing the tool (when loading from existing JSON!)
- and we need a wrapper (a HTML element) to store the UI of this tool
Then we need to define how to store data into the output JSON, so we define save method
save(blockContent) {
return {
latex: blockContent.value,
};
}
The blockContent is what the render method returns. We'll look at that part now
render() {
this.wrapper = document.createElement("math-field");
this.wrapper.setValue(this.data.latex);
this.wrapper.macros = {
RR: "\\mathbb{R}",
};
this.wrapper.mathVirtualKeyboardPolicy = "sandboxed";
this.wrapper.addEventListener("focusin", (evt) =>
window.mathVirtualKeyboard.show()
);
this.wrapper.addEventListener("focusout", (evt) =>
window.mathVirtualKeyboard.hide()
);
this.wrapper.addEventListener("keydown", (e) => {
const navigationKeys = [
"ArrowLeft",
"ArrowRight",
"ArrowUp",
"ArrowDown",
"Home",
"End",
"Backspace",
"Delete",
"Enter",
"/",
];
if (navigationKeys.includes(e.key)) {
e.stopPropagation();
}
});
return this.wrapper;
}
This function is quite long, but let's break it down
- We assign the HTML element
math-fieldto the wrapper - Set the value of the math-field to the LaTeX formula loaded from data (which can be
undefined) - Define macros for LaTeX input
- Configure the policy and focusin/focusout event handlers to automatically open the virtual keyboard when the user focuses on the math-field
- Add an event listener to intercept keys that would otherwise cause you to lose focus on the math-field (remember that editor.js is an editor, and those keys would trigger other operations in the background editor)
- Finally, we return the wrapper, this HTML element will be the UI element of this tool
At the end, remember you also need to import css of mathlive in HTML
<link rel="stylesheet" href="https://cdn.jsdelivr.net/npm/mathlive/mathlive-static.css" />
How to package Mathlive JS code depends on your bundler - that's an entirely separate issue that I won't cover here.
Now that the technical details are covered, I can discuss the motivation. Basically, most editors split math formula input into two phases: When you focus on it, it show the original LaTeX syntax so you can edit it. When you focus out, it use KaTeX to render the formula result. But that's messy!
This model makes it easy to miss small problems, that's why there are many small typos in complicated formulas. WYSIWYG is the tool to solve this, and mathlive is such editor I need.
The full plan - though I'm not sure if I'll actually do it - is a complete note-taking system for academic knowledge. Some great tools include forester, Heptabase, Obsidian, etc. However, they all have some rough edges for example
- forester has no editor part (there are some external editor projects though)
- I can't contribute to codebase of Heptabase
- Obsidian's format in long period is problematic
- An Obsidian editor extension can't be ported to non-markdown formats, so notes taken here can't be ported to forester, for example
I have to say these aren't problems with the tools themselves, but I do want a tool that has WYSIWYG + portable format (JSON is good enough) + searchability.
Of course, to keep learning progress of mine, I can't spend all the time on a tool - working on problems and reading papers are much more important for learning.
sauron supports find references in project [programming-0003]
sauron supports find references in project [programming-0003]
sauron now supports find references of a definition in a whole project scope at commit: 3f78957a. This is a final piece of my IDE development for Racket, I had this idea three years ago, but get completed till now. This is because the resource stability of Racket get a huge improved, make this possible, I don't have detailed number, but the same program three years earlier will take down DrRacket.
After the above nonsense, I should quickly explain the idea, it can be break to a few steps
Everytime the project-directory is change (this is a configuration item), send update command to files' maintainer
In each collector, record entries of reference like this: key is filename of definition and identifier of definition, value is the binding location (filename, start, and end position)
When user use Cmd+B/Click, check the cursor is on a definition or on a binding. If cursor is on the later, open list-box to pick a reference/binding, and the selection will bring user to a new location
Now, let's look at the result: a definition in a.rkt, a provide and a local reference/binding, and a reference from another file b.rkt. Three references are showed in the list-box
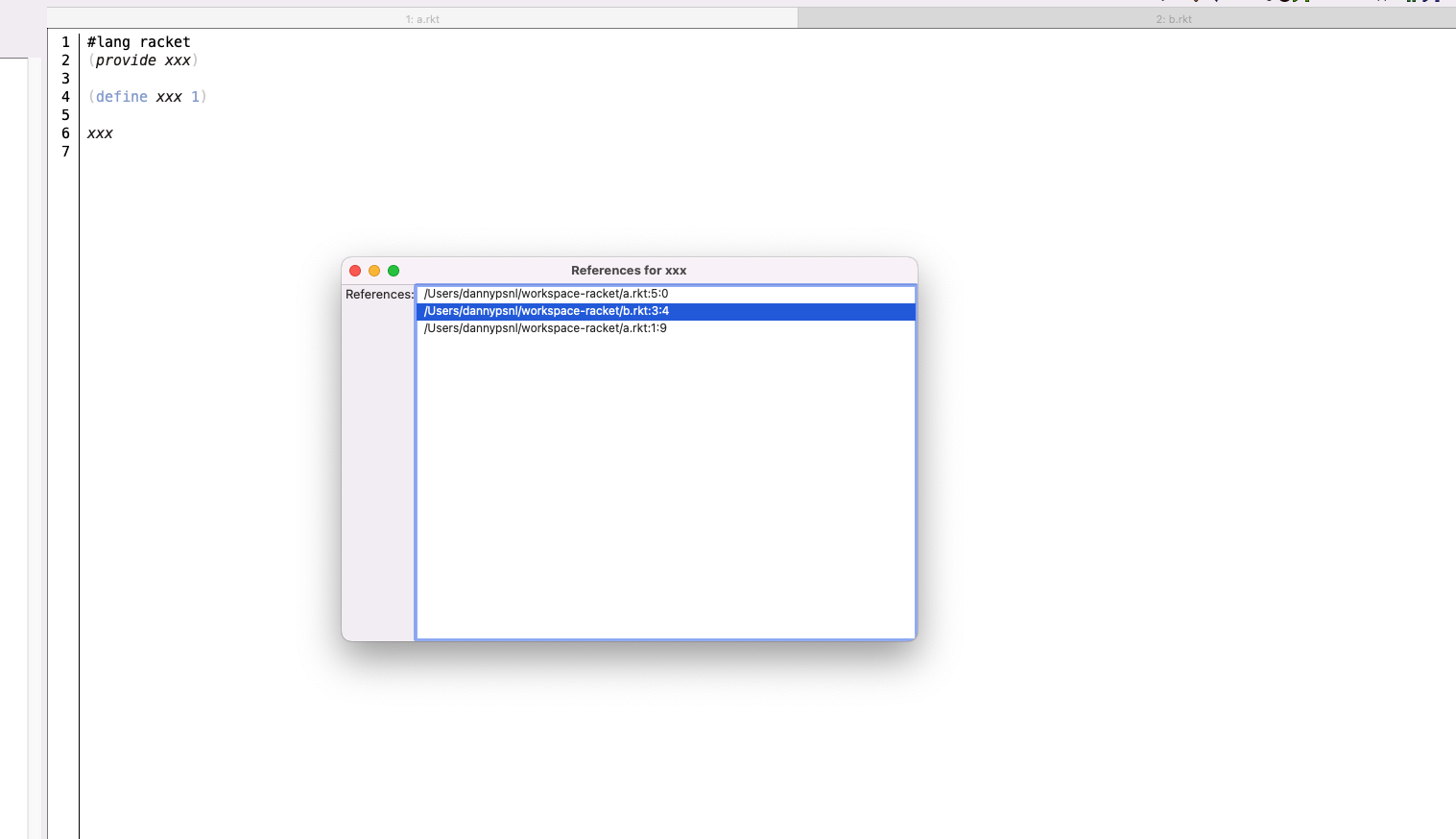
After click the item, the frame move to binding location at b.rkt.

Anyway, this is a nice end for this project, in the future I will more focus on racket-langserver because it can help more users.
TeXmacs [software-0008]
TeXmacs [software-0008]
最近因為朋友提及,所以真正嘗試了 TeXmacs https://www.texmacs.org/ 這個軟體,感受到什麼是所見即所得應有的樣貌,於是想寫下一點介紹。由於 TeXmacs 做的特別好的是數學公式編輯,所以我們集中在這件事上。在 TeXmacs 中輸入 $ 就會立即創造一個 math 區塊,用 Ctrl + $ 則會創造置中的 math 區塊($ 係指 Shift + 4,本文的快捷鍵皆為 MacOS 上的情況,在其他系統需注意差異)。
cursor 的所在區塊會被淺藍色框標記,範例如下

被選擇的區塊,會用紅色標記。用鍵盤或是滑鼠都可以選取

在 math 區塊中輸入分數時,鍵入 \frac 然後按下 Space,就會出現上下兩個區塊

其中紫色的是 cursor,可以用上下鍵切換要在哪個區塊繼續輸入

次方也是同理
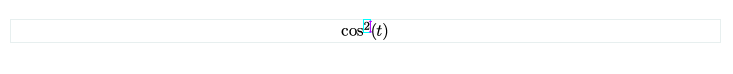
對於等號,也有特殊的操作可以使用,比如選擇等號後按下 Ctrl + A,就會在正上方出現輸入區塊


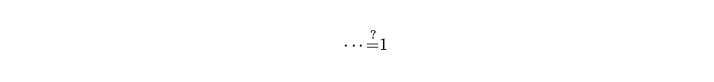
最後,還有一些數學常見的段落,都已經寫成樣板可以直接插入:
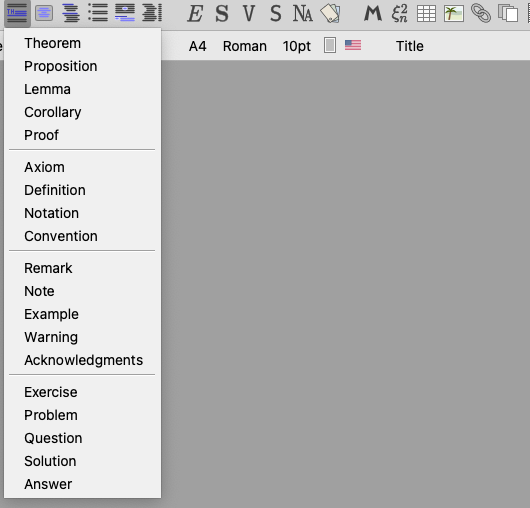
插入結果

My exploring Borsuk-Ulam Theorem [math-000U]
My exploring Borsuk-Ulam Theorem [math-000U]
My exploration (around April, 2025) of Borsuk-Ulam theorem began with trying to prove the Lyusternik-Shnirel'man closed theorem for and . While I could grasp it intuitively, constructing a rigorous proof proved elusive.
This led me to tackle the Borsuk theorem directly: For every continuous function , there exists a point such that .
The Failed Stereographic Approach
My initial idea was to decompose using North/South stereographic projections—the natural atlas for . This approach not quite work here: the N/S maps send the projection point to nowhere (or must change codomain to one-point compactification), making any function decomposed this way necessarily discontinuous.
Refinement: Finite Projections
I then considered pulling the projection point outward along the N-S axis, forcing projections into finite regions to maintain continuity. This insight—that continuity constraints force us to work in bounded regions—became crucial to my understanding.
Following this idea to examine the N/S map decomposition, after compressing infinity back to , the continuity requirement also necessitates pulling back the neighborhood, leading to the same conclusion as the outward projection: the region must be finite.
At this moment, I learn the relations between different description of Borsuk-Ulam (Some applications of the Borsuk-Ulam Theorem).
The Breakthrough
My proof strategy ended up opposite to the classical development. I first established a lemma:
Lemma: Let be continuous and antipode-preserving. Then there exists such that .
The details can be found here, the key is bound an open set of that contains and is the image of rest two open sets on . Hence, for some
The Proof
For the main theorem, define . Two key observations:
- is continuous
- is antipode-preserving:
Applying the lemma: there exists such that , which means , hence . Proof complete.
The "wrong" approach turns out is useful in lemma, and provides a more concrete view about the problem.
After this, I also found Borsuk-Ulam Implies Brouwer: A Direct Construction, which is the same approach, and use cube version.
Determinant 的意義 [math-000Q]
Determinant 的意義 [math-000Q]
從矩陣非常難看出 determinant 的意義,但它其實具備幾何的意涵:對 個向量張出的高維平行體的體積影響。
矩陣 可以視為張量 ,向量張出的高維平行體可以表示為 exterior product 。因此定義 如下:
這表示 把 映射到 所得的新高維平行體的體積相對於先前的高維平行體的比例(可能會正負轉換)。
補充:當 時。 階 skew-symmetric tensor 的空間 很明顯只有一個維度,這個空間在 Lectures on the Geometry of Manifolds 中叫做 Determinant line of 。此時 全都是 trivial space(只有 元素)。
部落格遷移 [blog-0000]
部落格遷移 [blog-0000]
最近終於自己寫了個 site generator tr,這套機制確實是解決我很多問題,所以就開始遷移舊的部落格了。原則上大部分文章或是筆記都不會跟過來,因為這也是趁機丟掉一些已經過時/太簡單的筆記的機會,tr 讓我可以直接嵌入 wiki/nLab 來取代解釋基礎的定義。
NixOS 需要定期清除 generations [software-0000]
NixOS 需要定期清除 generations [software-0000]
這是今天遇到的問題,更新系統時它提示 /boot/ 的空間不足以安裝 efi 檔案了,直接砍 /boot/EFI/nixos/ 裡面的檔案是沒有用的,因為 NixOS 的 generations 會重新生成這些資料。所以正確的作法是先執行下面的指令
cd /nix/var/nix/profiles
裡面會有很多像是 system-數字-link 這樣的 soft links,每一個對應一個 NixOS 的 generation。把太古老的 generations 刪掉,執行
nix store gc
這會跑一段時間(如果你跟我一樣太久沒有清理就需要很久),結束之後再次更新系統就可以了。
何謂 elaboration? [cs-0004]
何謂 elaboration? [cs-0004]
elaboration 指的是轉換沒有語意的表面語法(surface syntax 或是說 source code)到有語意的語言表示(language representation)的過程,這樣講可能有點抽象,所以需要一些例子。試問 foo(a, b) 這段 Go source code 有語意嗎?事實上是沒有,因為只有在 Go compiler 經過
- 讀取文字
- 解析語法取得語法樹
- 型別以及其他檢查
現在這段程式碼才會在 Go compiler 內部用某種資料結構表示,而 Go compiler 可以相信這段程式碼是滿足 Go 規範的程式,這樣才是有語意的語言。這個觀點一開始對你來說可能蠻怪異的,但我們可以仔細來看這樣定義的好處
- 有些語言如 Fennel https://fennel-lang.org/ 刻意把自己變成另一個語言 Lua 的另類文法,在語言表示層面要求共用一樣的語意。Fennel 還支援了 macro 系統
- 語法可以作為片段,嵌入到任何位置,只不過後續的檢查階段可能拒絕嵌入後產生的語法,因為這樣產生的程式依然可能是語法或是語意不正確的,比如使用 C 語言的 preprocessor 寫程式就經常會遇到這樣的問題。能把語法記錄下來並在別的地方展開的程式就叫做 macro,LISP 的 elaboration 經常叫做 expander
Macro system [cs-0005]
Macro system [cs-0005]
雖然 C 的 preprocessor 也被稱為 macro,但跟 LISP、Elixir、Julia 比起來就差很多的原因是
- C 對語法的原始位置放棄追蹤
- C 對 macro 的輸入跟輸出都沒有基本的檢查,也沒辦法對不同輸入做出反應
而常見的 LISP macro 過程則是:
- reader:
TEXT -> S-expression - 使用者定義的 macro:
S-expression -> S-expression - expander:
S-expression -> LISP
elaboration 前對語法樹進行操作的能力就是 LISP 最大的特徵,這使語言使用者可以自行發展他想要的語法,Clojure 做得比傳統 LISP 更好的地方就是這裡它採用的 edn 能表示比 S-expression 更多的資料,如 hashmap。
什麼是 subroutine? [cs-0006]
什麼是 subroutine? [cs-0006]
subroutine 在 C 語言被稱為 function,Fortran 中則分出 function 或是 subroutine,剩下還有一些語言使用 procedure 這個名稱。
Fortran offers two different procedures: function and subroutine. Subroutines are more general and offer the possibility to return multiple values whereas functions only return one value. https://fortranwiki.org/fortran/show/procedure
我把定義 subroutine 為一個指令語言編寫程式的模式,在組合語言裡面,我們並沒有函數名稱這種東西,相對的,其實只有指令的位址,所以組譯語言通常會提供區塊名稱來標記位址,比如 a:,那你可能已經想到了,如果我跳轉到 jump a 是不是就能執行 a 的內容了!是,但你要怎麼跳回來呢?所以 subroutine 就被發明了:找個 register 放一下要跳轉回來的位址就好啦!於是一個 a 呼叫 b 的程式就寫成
a: store ret (here+1) jump b ... b: ... jump ret
(here+1) 是為了跳過 jump b 這個指令,而 ret 就是一個特殊保留的 register,專門用來讓 subroutine 使用。你會發現,ㄟ這樣是不是沒有傳遞參數?沒錯,所以更完整的故事是,CPU 會乾脆設計一整套傳遞參數應該用哪幾個 registers 跟 stack 偏移的慣例,叫做 calling convention。
這就是所謂的現代 CPU 是為了 compiler 設計。不遵守這些慣例你的程式還是能動,但你的程式就會跟其他 compiler 為這個 CPU 吐出來的程式很難溝通。
作業系統的行程排程 [cs-0007]
作業系統的行程排程 [cs-0007]
在一些非常簡單的作業系統實現裡面,會乾脆讓 user process 自己決定要不要讓出 CPU,怎麼讓?就是把自己當前的 stack pointer address 以及 registers 狀態儲存到記憶體裡面去,通常是 kernel 提供的一個 struct,然後跳轉到另一個 process 去。
這樣的話這是 user process 自己決定讓給誰,一般其實也不是這樣實現的,而是 user process 只有呼叫 yield 把自己暫停,下一步轉移給誰交給 kernel 決定。比如 Linux 就有
int sched_yield(void)
這個函數。
但要是 user process 不小心陷入無限迴圈怎麼辦?所以更常出現的是所謂的搶佔式排程,kernel 分配 time slice 並且封裝 process,並且設定計時器硬體中斷來確保自己可以定時查看狀態,這樣 process 在 slice 用光之後(或是它的指令執行完畢)就可以被切斷。
Transformation induced dual basis [math-000D]
Transformation induced dual basis [math-000D]
Manifolds and Differential Geometry
Let be a basis of vector space , and let be a basis of dual space . Now if is another basis of , then there is an induced basis for dual space .
Proof
By Kronecker-delta
can see that if then the equality is hold. We can use Penrose notation to show the idea.
Algorithm. Elaboration zoo 中的合一演算法與隱式參數 [tt-0006]
Algorithm. Elaboration zoo 中的合一演算法與隱式參數 [tt-0006]
程式語言為了讓使用者省略不必要的輸入,必須為使用者推導內容,這種需求催生了合一這種類型的演算法。比如很多程式語言允許泛型,比如下面的 OCaml 程式碼
let id (x : 'a) : 'a = x
Elaboration zoo 這個教學專案,它的程式碼要解決的,是一類更複雜的程式語言,叫做 dependent type 的系統中的合一問題,這類系統最重要的特性,就是類型也只是一種值,值也因此可以出現在類型中,但這就比較不是本篇的重點,有興趣的讀者可以閱讀 The Little Typer 來入門。在解釋完它的合一之後,我會介紹它隱式參數的解決方案
Algorithm. 合一演算法的過程 [tt-0007]
Algorithm. 合一演算法的過程 [tt-0007]
假設有程式碼
let id {A : U} (x : A) : A := x
let id2 {B : U} (x : B) : B := id _ x
這裡 id _ x 中的底線表示「省略的引數」,被稱為 hole,我們並沒有明確的給它任何值,比如 B。在展開這個 hole 時,我們用 meta variable ?0 替換它。但 meta variable 必須考慮 contextual variables 的 rigid form,因此進行套用得到 ?0 B x。這引發問題
什麼是 contextual variables?為什麼 contextual variables 是 B 與 x? [tt-0009]
什麼是 contextual variables?為什麼 contextual variables 是 B 與 x? [tt-0009]
答案是,這些是 ?0 能看到且實際內容未知的變數,只能用 rigid form 替代
什麼是 rigid form? [tt-000A]
什麼是 rigid form? [tt-000A]
rigid form 是 dependent type 中即使是 open term 也必須先進行計算而被迫在實作中出現的一種值;由於 meta variable 而被迫出現的值則叫做 flex form
現在我們手上有的 term 是 id (?0 B x) x,現在執行 id (?0 B x),我們得到型別為
的 term
注意到 中兩個 來源不同,不可混用,我用顏色表示它們的 scope 其實不同這件事
現在進入到把這個 term 套用到 x 上的環節了,因此觸發 是否是 的 term 的合一計算,我們概念上紀錄成
現在合一演算法必須找出合適的 來滿足等式。我們知道 應該是某種 lambda
,顯然 就會給出我們想要的答案,但這部分要怎麼做到?elaboration zoo 的演算法分成三個階段
Invert [tt-000B]
Invert [tt-000B]
這裡的重點是,既然 已經套用了 與 ,因此就創立關聯它所創立的 lambda 中的變數到其 contextual variables 的映射(mappings)是
Broken pipe (os error 32)現在右手邊的 term 只需要看自己的每個 rigid form 有沒有被指向,只要這個映射裡面查找到有變數是指向 rigid form 自己,即反過來創立 rigid form 指向新名字的映射。比如說我們右手邊的 term 是一個 rigid form ,因此得到的反映射是
Rename [tt-000C]
Rename [tt-000C]
在上一步中得到的反映射是
用這個映射去改寫右手邊 term 的內容,就得到等式 ,而解則是 。
Lambda 化 [tt-000D]
Lambda 化 [tt-000D]
最後真正構造一個 lambda abstraction,就得到了
安插隱式參數的方法 [tt-0008]
安插隱式參數的方法 [tt-0008]
在最開始的程式碼
let id {A : U} (x : A) : A := x
let id2 {B : U} (x : B) : B := id _ x
裡面,其實 {} 中的綁定叫做隱式參數,這表示我們其實也可以用 id x 來調用該函數。但這時候要怎麼知道需要補一個 hole 進去呢?elaboration zoo 作者提出的簡易方案就是區分 implicit type 與 implicit application,如此一來,當一個 implicit type 被 explicit apply 的時候,我們就知道要安插 hole 了
以 id x 而言,如果要明確的用 implicit 調用它,就必須寫成 id {B} x,在語法就進行明確的區分。
這時候跳回去看「contextual variables 是 能看到且實際內容未知的變數」就更能了解其理由了,因為已經能明確知道其內容的變數,如
let x = t
x 就是指向 t 的情況,若右手 term 是 x,其實也會是 t 去進行 unify。若右手 term 已經是 rigid form 又可參照,就更不需要成為 contextual variables,因為其 solution 就是把右手 term 原封不動放入,在反轉 map 的時候,只要記得這個 rigid 是非 contextual,就可以為它寫一個 identity mapping。
相關:higher-order-unification/explanation.md at master · jozefg/higher-order-unification --- github.com
racket 中的有界續延如何實作 effect system 的功能? [cs-000G]
racket 中的有界續延如何實作 effect system 的功能? [cs-000G]
討論如何用 racket 中的 continuation 實作 effect system 的概念
一個 effect system 大概做了什麼,我們從 effekt 語言 (https://effekt-lang.org/) 這個案例著手
- 一個簽名
effect yield(v : Int) : Bool - 一個 handler
try { ... } with yield { n => ...; resume(n < 10) } - 在
try區塊中調用的函數f可以用do yield(k)來調用 handler - 當
f執行到do yield(k),就會跳轉到with yield中繼續進行,並且n = k - 當程式執行到
resume就會跳回去f之後的do yield(k)的續延繼續執行
因此 exception 系統也可以被視為,沒有調用 resume 的 effect handler,讀者或許也想出數種使用方法了吧?這正是 effect system 的價值。而 racket 擁有比 effect handler 更複雜的機制(continuation with marks),不過 effect handler 機制具有保障使用者不容易出錯的好處,因此在 racket 中模擬一套 effect system 依然有意義,也是有趣的挑戰。
call/prompt [rkt-0000]
call/prompt [rkt-0000]
call/prompt 的主要功能,就如其名稱,是為被呼叫的函數提示一個標記,這個標記在 abort/cc 會被使用。完整的 call/prompt 調用是
(call/prompt f tag handler args ...)
f 是被調用的函數,中間的 tag 是標記,handler 是處理標記的函數,剩下的都是 f 的參數。讀者可以想像成
(with-handler [tag handler] (f args ...))
abort/cc [rkt-0001]
abort/cc [rkt-0001]
abort/cc 的調用是
(abort/cc tag vs ...)
tag 當然就是先前 prompt 寫進去的 tag,而 vs ... 則作為呼叫 handler 的引數
(handler vs ...)
Continuation prompt tag 的產生方式 [rkt-0002]
Continuation prompt tag 的產生方式 [rkt-0002]
調用 (make-continuation-prompt-tag) 產出,這個函數還可以接受一個 symbol 產生可讀的識別碼,並且每次調用這個函數,產生的 tag 都算是不同的 tag,勿必要儲存好這個實體。
要想實現 exception 目前的程式已經完全充分了,只要寫下
(define (f params ...)
(abort/cc tag "cannot read file ..."))
(call/prompt f
tag
(λ (err)
(printf "got err ~a~n" err))
args ...)
即可。事實上 racket 自身的的 exception 也是這樣實作的,要考慮的問題是,前面我們看過 resume 可以跳回去被呼叫的函數!這是如何做到的?
call/cc [rkt-0003]
call/cc [rkt-0003]
call/cc 這個函數是 call with current continuation 的意思,比如說在下面的程式碼中
(* 2 1)
1 的 continuation 就是把 1 挖掉留下的 (* 2 hole),故下列程式碼
(* 2 (call/cc (λ (k) (k 1))))
的結果是 2。讀者可以想像 k = λ (hole) (* 2 hole),這在實作上不太正確,但對理解很有幫助。
一般來說,racket 的函數會簡單的寫成
(define (f params ...) stmt1 ... stmtn)
如果我在其中安放一個 call/cc 會發生什麼事呢?
(define (f params ...) ... (call/cc (λ (k) ...)) stmtk ...)
答案是 k = λ () (begin stmtk ... stmtn)。由於 racket 自動把
stmt1 ... stmtn
包裝成 (begin stmt1 ... stmtn),而
(begin stmt1 stmt2 ...)
中 stmt1 的 continuation 是 (begin stmt2 ...),以此類推就很容易理解 k 等於什麼了。
我們正是需要使用 call/cc 來做出 resume 的效果。
實現 resume [cs-000H]
實現 resume [cs-000H]
在 f 中我們寫下
(define (f params ...) (call/cc (λ (k) (abort/cc tag k ...))))
在 call/prompt 的 handler 中新增一個 resume 參數,這樣就完成了。讀者可以填補下面的程式中的空白來檢驗結果,也充當練習
(define (f params ...)
(call/cc (λ (k) (abort/cc tag k ...)))
...)
(call/prompt f
tag
(λ (resume ...)
...
; 跳回 f 繼續
(resume))
args ...)到這裡我們已經有了運行的基礎,要改善有幾個方向可以參考
- 用 macro 包裝語法
- 放到 typed/racket 中加上 effect 類型檢查確保使用者沒有漏掉 handler:typed/racket eff
- 支持 finally handler,保證任何退出行為都會被這個 handler 攔截(考慮 racket 的函數
dynamic-wind)
使用 TLA+ 的第一步 [tla-0000]
使用 TLA+ 的第一步 [tla-0000]
由於很多 TLA+ 入門教學似乎都沒有談到實務上要從哪裡開始使用 TLA+,所以這裡我想介紹實際上要怎麼做。一個 TLA+ 的檔案以 .tla 為副檔名,其中由 --- MODULE name --- 開頭,由 === 結尾,例如
---- MODULE plustwo ---- =====
在其中可以引用模組,寫成 EXTENDS xxx, yyy, ...
---- MODULE plustwo ---- EXTENDS Integers =====
使用 PlusCal 語言 [tla-0001]
使用 PlusCal 語言 [tla-0001]
比起直接寫出 Spec 等不變式,先寫 PlusCal language (https://lamport.azurewebsites.net/tla/tutorial/intro.html) 的程式再使用用它生成的 Spec 不變量會更簡單也更實用。因為 TLA+ 會嘗試生成所有可能的狀態,有可能出現所謂的 unbound model (https://learntla.com/topics/unbound-models.html),就結果而言對它進行檢查永遠不會完成。用 PlusCal 語言寫的程式相對容易發現這種錯誤。
---- MODULE plustwo ----
EXTENDS Integers
CONSTANT Limit
(* --algorithm plustwo
variables x = 0;
begin
while x < Limit do
x := x + 2;
end while;
end algorithm; *)
\* BEGIN TRANSLATION (chksum(pcal) = "3f62e9ff" /\ chksum(tla) = "239a9ecd")
\* END TRANSLATION
=====
由 PlusCal 產出的不變量會被包在 BEGIN TRANSLATION 到 END TRANSLATION 裡面,可以發現它還會檢查 checksum。由於這個區塊內的程式會被機器生成的內容覆蓋,因此千萬不要把自己寫的不變量放在這個區塊中。
上面的 CONSTANT Limit 可以在 model 的設定檔 .cfg 中指定,這是為了避免把常數寫死在 TLA+ 主程式中,好在檢查前可以進行修改。
增加不變量 [tla-0002]
增加不變量 [tla-0002]
在有了這些程式之後,可以開始增加自己的不變量
Even(x) == x % 2 = 0 IsInc == x >= 0 Inv == IsInc /\ Even(x) THEOREM Terminated == Spec => Termination
IsInc要求x總是大於初始值0Even(x)要求我們寫的程式只會產生偶數Inv把所有我們想證明的不變量組合在一起,/\表示邏輯的「a 且 b」語句。我想很容易猜到\/表示邏輯的「a 或 b」語句
THEOREM 部分宣告 Spec 蘊含 Termination 不變量,這兩者都是 PlusCal 產生的,所以不用太在意細節,這裡的意義是證明程式確實會終止。
這裡介紹了 TLA+ 如何運作,TLA+ 對現實程式的幫助會體現在編寫非同步的程式時,TLA+ 擅長對只有有限狀態、可以使用經典邏輯推導的程式進行檢查,主要可以發現死鎖與違反不變式等錯誤。對 TLA+ 所使用的數學方面的學習可以參考 Lamport 本人寫的 A Science of Concurrent Programs。
The concept of webmention [webmention-0000]
The concept of webmention [webmention-0000]
Each web page should provide the following content (use my site dannypsnl.me as example) in
<link href="https://dannypsnl.me/webmention-endpoint" rel="webmention" />
sender view [webmention-0001]
sender view [webmention-0001]
According to webmention spec, if someone tries to notify my site that there is a link mentions my post, she has to do the following:
curl -I https://dannypsnl.me/xxxto get my webmention endpoint in thehead- post the data, where
is the link refers to my postPOST /webmention-endpoint HTTP/1.1 Host: dannypsnl.me Content-Type: application/x-www-form-urlencoded source= target=https://dannypsnl.me/xxx
receiver view [webmention-0002]
receiver view [webmention-0002]
Therefore, a receiver is a POST handler. According to spec, we can
- return http code
201withLocationin header pointing to the status URL - return http code
202and asynchronously perform the verification - return http code
200and synchronously perform the verification (not recommended), by section 3.2.2Webmention verification should be handled asynchronously to prevent DoS (Denial of Service) attacks.
Verification
- The receiver must check that
sourceandtargetare valid URLs [URL] and are of schemes that are supported by the receiver. (Most commonly this means checking that thesourceandtargetschemes are http or https). - The receiver must reject the request if the
sourceURL is the same as thetargetURL. - The receiver should check that
targetis a valid resource for which it can accept Webmentions. This check should happen synchronously to reject invalid Webmentions before more in-depth verification begins. What a "valid resource" means is up to the receiver. For example, some receivers may accept Webmentions for multiple domains, others may accept Webmentions for only the same domain the endpoint is on.
If the receiver is going to use the Webmention in some way, (displaying it as a comment on a post, incrementing a like counter, notifying the author of a post), then it must perform an HTTP GET request on source, following any HTTP redirects (and should limit the number of redirects it follows) to confirm that it actually mentions the target. The receiver should include an HTTP Accept header indicating its preference of content types that are acceptable.
Error response
If the Webmention was not successful because of something the sender did, it must return a 400 Bad Request status code and may include a description of the error in the response body.
However, hosting a receiver can be annoying, so we should build on the top of some existed tools.
無外部空間下如何考慮幾何空間的測量? [math-0001]
無外部空間下如何考慮幾何空間的測量? [math-0001]
metric 就是在測量長度。不過在歐式空間裡面討論嵌入其中的曲面時,曲面有外部空間切向量,也就是歐式空間的向量可以使用。如果曲面沒有外空間,就需要自己做一個出來,這就引出了 Riemann metric 的想法:對可微分流形 的每一點 考慮抽象的切空間 (不考慮 到底是什麼),重點是隨點附上內積函數 ,因為是模仿內積所以有 bilinearity, positive-definiteness, symmetry 等性質
現在考慮曲線 ,在每一點度量 向量並積分(加起來)即是曲線長度。又隨著區間 改變,會有對應變化的 點,因此模仿並定義
是 norm 的定義,積分因為是跟著 變化,因此依賴 的參數 來定義。如此一來就可以問下一個問題:根據 是從 到 的最短曲線是誰,這就是曲面上的直線的概念(然而,全域與局部最短線,是不一樣的問題,考慮整體將會複雜許多)。
https://qi.bookwar.info/pi-day-special-manifold 對 Manifold 這個想法的高層次概念進行介紹。
Soundness and completeness [math-0000]
Soundness and completeness [math-0000]
- Classical logic's soundness says, if , then is classically valid.
- Classical logic's completeness says, if is classically valid, then .
可以看到,要用 soundness 與 completeness 時,是在關心特定屬性 p,我們說一個系統 sound 就是在問「系統能導出的結果是否滿足 p」;我們說一個系統 complete 則是在問「滿足 p 的結果是否皆能從系統導出」。
understanding -algebra [math-000E]
understanding -algebra [math-000E]
To understand -algebra, we will need some observations, the first one is we can summarize an algebra with a signature. For example, monoid has a signature:
or we can say ring is:
The next observation is we can consider these as objects in a proper category , at here is a [cartesian closed category](math-000D). For example
- monoid is a -morphism
- ring is a -morphism
Now, we generalize algebra's definition.
Definition. -algebra (algebra for an endofunctor) [math-000F]
Definition. -algebra (algebra for an endofunctor) [math-000F]
With a proper category which can encode the signature of , and an [endofunctor](math-001T) , the -algebra is a triple:
where is a -morphism.
With the definition of -algebra, -algebras of a fixed form a category
Definition. category of -algebras [math-000G]
Definition. category of -algebras [math-000G]
For a fixed endofunctor in a proper category (below notations omit fixed ),
- the F-algebras form the objects of the category,
- morphisms are homomorphisms of objects , composition is given by functor laws.
A homomorphism is a -morphism makes below diagram commutes.
We can extra check identity indeed works.
There is a theorem about the initial object of the category.
Theorem. Lambek's [math-000H]
Theorem. Lambek's [math-000H]
The evaluator of an initial algebra is an isomorphism.
Proof
Let be an initial in the -algebra category, the following diagram commutes for any -object
Now, replace with , we have commute diagram
Then we consider a trivial commute diagram by duplicating the path
Combine two diagrams, then we get another commute diagram
By definition now we know is a homomorphism, and since is an initial, we must have
Therefore, we also have
so is the inverse of , proves is an isomorphism.
catamorphism [math-000I]
catamorphism [math-000I]
The theorem actually proves the corresponding -object of initial algebra is a fixed point of . By reversing with its inverse, we get a commute diagram below.
In Haskell, we are able to define initial algebra
newtype Fix f = Fix (f (Fix f)) unFix :: Fix f -> f (Fix f) unFix (Fix x) = x
View as constructor Fix, as unFix, then we can define m = alg . fmap m . unFix. Since m :: Fix f -> a, we have definition of catamorphism.
cata :: Functor f => (f a -> a) -> Fix f -> a cata alg = alg . fmap (cata alg) . unFix
An usual example is foldr, a convenient specialization of catamorphism.
anamorphism [math-000J]
anamorphism [math-000J]
As a dual concept, we can draw coalgebra diagram
and define anamorphism as well.
ana :: Functor f => (a -> f a) -> a -> Fix f ana coalg = Fix . fmap (ana coalg) . coalg
I mostly learn F-algebras from Category Theory for Programmers, and take a while to express the core idea in details with my voice with a lot practicing. The article answered some questions, but we always with more. What's an algebra of monad? What's an algebra of a programming language (usually has a recursive syntax tree)? Hope you also understand it well through the article and practicing.
Theorem. A space is Hausdorff iff its diagonal map is closed [math-000B]
Theorem. A space is Hausdorff iff its diagonal map is closed [math-000B]
The proposition says a space is Hausdorff if and only if its diagonal map to product space is closed, which given an alternative definition. Notice that close means its complement is open. The definition of is
Not hard to see below argument also applies to all finite -product spaces.
Proof
(Hausdorff => diagonal map is closed) Hausdorff means every two different points has a pair of disjoint neighborhoods , where and . Therefore, every pair not line on the diagonal has cover them. The union of all these open sets covers , so the complement of the union is closed.
(diagonal map is closed => Hausdorff) Since
is open, which implies for all the pair . Since , this implies the fact that .
Also, for all and , it's natural that , since the open set at most cover .
Consider that reversely again, that means for all , pair (i.e. will not cover any part of diagonal), that implies as desired.
Lawvere's fixed point theorem 的陳述與應用 [math-0005]
Lawvere's fixed point theorem 的陳述與應用 [math-0005]
這篇文章試著介紹 Lawvere's fixed point theorem 的意義與應用
Theorem. Lawvere's fixed point [math-0006]
Theorem. Lawvere's fixed point [math-0006]
DIAGONAL ARGUMENTS AND CARTESIAN CLOSED CATEGORIES
在一個 cartesian closed category 中,如果 是 point-surjective,則所有 都存在不動點 (滿足 )。
Proof
首先畫出交換圖
其中 的定義是 ,所以對 來說 。沿著這個定義,我們知道 。根據 point-surjective 我們知道 對每個 來說都是唯一確定的。現在把往下方 的 也畫出,即可得出等式:
換句話說 的不動點即是
Example. 應用到 lambda calculus [math-0007]
Example. 應用到 lambda calculus [math-0007]
編碼的方式是找一個只有兩個物件 的 category ,讓 lambda calculus 的 terms 是 -morphisms,這些技巧在 Categorical semantic 領域內相當常見。
到這裡必須檢查 lambda calculus 確實存在 point-surjective,歡迎自行嘗試。
按此編碼後可以得到 。套到等式上
可以得到以下編碼
把 改寫成 ,於是等式可以寫成 ,而函數套用語法可以用 退化,於是得到
注意到 的定義是非遞迴的,因此一定是可定義的。
計算即可發現確實 。因為所有的 -term 都屬於 ,所以現在我們知道任何 lambda calculus 的函數都有不動點。
Example. 應用到 Cantor's theorem [math-0008]
Example. 應用到 Cantor's theorem [math-0008]
取 category 並令 就可以證明 [Cantor's theorem](math-0059)。我們需要引理
Lemma. no point-surjective morphism [math-0009]
Lemma. no point-surjective morphism [math-0009]
If there exists such that for all , then there has no point-surjective morphism can exist for .
This is a reversed version of Lawvere's fixed point, no need an extra proof.
Proof
存在 令所有 都滿足 ,所以對任何集合 都不存在 的 point-surjective 函數,因此也不存在 。
這個定理也可以用到 Gödel incompleteness、Tarski definability 等等問題上。論文 Substructural fixed-point theorems and the diagonal argument: theme and variations 更進一步的簡化了前置條件。
子類型與多型(泛型) [tt-000L]
子類型與多型(泛型) [tt-000L]
這個文章源自下面的問題
不過想問問專業的⋯⋯Golang 都有 interface 這種東西,提供泛型的必要性是什麼啊?
這是個常見的誤解,因為大部分語言不會多認真跟你講清楚到底啥是啥,看來好像都能接受多種不同的類型輸入不是嗎?所以這裡我們就來看各種機制的定義跟差別。
Go 的 interface [tt-000M]
Go 的 interface [tt-000M]
Go 語言的 interface,範例如下
type Abser interface {
Abs() float64
}
其中的 Abs() float64 可以被改寫成抽象語法 Abs : () -> float64。因此一個 interface 有一組與其關聯的一系列簽名 。並且,對 Go 而言下列的兩個 interface 並沒有差異
type A interface {
F(C) D
}
type B interface {
F(C) D
}
因此我們可以更進一步認為 Go 的一個 interface 可以完全由其簽名 替換。
Java 的 interface 與 bounded polymorphism (bounded quantification) [tt-000N]
Java 的 interface 與 bounded polymorphism (bounded quantification) [tt-000N]
在 Java 之中可以定義 interface,範例如下
interface Comparable{ int compareTo(T other); }
相較於 [Go 中不用明確宣告](tt-000D),在 Java 中實現 interface I 需要寫成 class T extends I,因此雖然 Java 的 interface 也有其相關的一組簽名 ,但兩個有同樣簽名 的 interface 不是同一個型別。
而在 Java 中 bounded polymorphism 指的是以下的 interface 使用方法:
<S extends Comparable> S min(S a, S b)
這會使得沒有明確宣告實現 Comparable 的型別無法被傳為 min 的引數。
問題所在 [tt-000O]
問題所在 [tt-000O]
現在考慮一個簽名
在 Java 裡面可以確實保證兩個參數跟回傳的型別都是同一個。在 Go 裡面這個簽名就只能寫成
而兩個參數跟回傳的型別不一定相同。現在我們就會發現乍看之下 interface 對類型的約束跟多型一樣可以被多個不同的型別滿足,但事實上根本就是不同的東西。
interface 是一種子類型關係,換句話說當 實現 我們就說 ,在每個要求 的位置都可以用 取代。
多型的本體是一個型別等級的參數!在語意學上,上面的簽名可以改寫成 ,當你寫下
的時候,乍看之下是一個完整的呼叫。實際上編譯器會先推導 的類型,記作 ,譬如假設 則 ,這時候就可以做型別替換 得出 。因此真正的呼叫程式碼是
子類型規則並不能取代替換這個語意。在 Java 的 規則下,僅是多檢查了 是否為真,子類型與多型仍然是不同的規則。
Gödel incompleteness theorem 到底證明了什麼? [math-0002]
Gödel incompleteness theorem 到底證明了什麼? [math-0002]
哥德爾不完備定理是一個相當有趣的邏輯學發現,要了解他的意涵,要先考慮哥德爾的編碼
哥德爾數(Gödel number)是一種編碼方式,在一個算術系統裡面,當我們把每個字符都排成一個有限的列,我們可以幫每個字符都指定一個自然數。具體來說,我們可能會寫下
- 是 ,其後設意義為「否定」
- 是 ,其後設意義為「或」
- 是 ,其後設意義為「且」
當有符號 ,其對應的哥德爾數為 。我們並不是真的關心具體的每個符號,我們做這件事的理由是為了表示哥德爾編碼。所以這裡要開始定義哥德爾編碼,首先先看一個簡單的例子:當有系統的公式符號排列 ,我們說公式的哥德爾編碼為 。
因此用函數 指示一個公式的每個位置 符號的 Gödel number,則哥德爾編碼確切的定義是
,也就是將質數以每個符號對應的哥德爾數為指數,將它們全部乘起來。這個辦法只是為了迫使每個公式有對應的編碼存在。我們用 記號表示公式 的哥德爾數。
函數給出第 個出現符號的在表中的位置。
在承認前述的系統 下,可以開始描述。
Definition. substitution [math-0004]
Definition. substitution [math-0004]
表示將公式 中哥德爾數為 之符號換成 的哥德爾數再求此替換後公式的哥德爾編碼。
例如
Theorem. Gödel incompleteness [math-0003]
Theorem. Gödel incompleteness [math-0003]
- 存在形式上不能證明卻是真確、可寫下的公式
- 用系統證明自身的一致性會導致不可決定的公式也被證明
Proof
首先,用 表示有哥德爾數為 的公式在系統 中得到證明,而 是其演示
哥德爾有一段很長的論證(證明這是原始遞歸函數),來說明這是可以被 表示的,這裡跳過了這部分論證。且這也是為什麼要求系統 是具備算術能的,因為表示編碼需要自然數算術。
定義 ,但 是未知量,隨意給一個還沒被使用來編碼的數字即可,比如 。於是我們重寫成 。
現在構造 ,求其哥德爾編碼 可以發現正是 所表示的編碼,因為
因此用 替換 中的 ,會得到
可以發現 的後設含義正是「有哥德爾編碼為 的公式沒有系統 中的證明」,然而
- 假設 可以在 中證明為真,就告訴我們 對應的公式不存在任何演示可以於 中證明,但那就是我們剛證明的公式 。
- 假設 可以在 中證明為否,就導出 對應的公式在 中有演示,但那就是我們剛證否的公式 。
綜合可知這意思就是 可證,若且唯若 可證否,是故承認 就是承認 不一致;反之,若 一致則 形式上就不可決定。
巧妙的是,並不難看出 的 meta 陳述是真確的,因為確實不存在任何整數作為編碼滿足這個性質。換句話說,存在形式上不能證明卻是真確、可寫下的公式,這就是第一不完備定理。接著根據第一不完備定理知道了 的真確性,卻在 中形式上不可決定,所以 不能證明一個真確的算術公式,因此 必定是不完備的,這就是第二不完備定理。
因此在 The Blind Spot: Lectures on Logic 中可以看到其陳述更加關注核心:對一個足夠編碼自己又一致的系統
- 存在一個真確的公式 不可決定
- 系統證明自己具有一致性會連帶證明這個不可決定的公式,所以系統無法證明自己的一致性
換句話說,要關心的並不是具體如何構造上面陳述的編碼,而是這類系統編碼系統自身的普遍性問題。
型別有多大? [tt-000E]
型別有多大? [tt-000E]
不久之前看到fizzyelt 的文章,所以我前幾日開始研究自己以前寫的 strictly positive 筆記,因此找到了 Andrej Bauer 在 stackexchange 的回答,整理後寫了這篇文章解釋何謂型別的大小
型別的大小 [tt-000F]
型別的大小 [tt-000F]
要了解型別的大小的意義,可以先考慮一個 small cartesian closed category ,令型別是範疇 的物件(視為只有一個型別的 context)。
應用 slice category [tt-000H]
應用 slice category [tt-000H]
在這個情況下,對任意型別 ,slice category 表示「到達 的 morphism」所構成的範疇,也就是 的 objects 與 triangle morphisms。
Example. 從 出發 [tt-000I]
Example. 從 出發 [tt-000I]
接著,我們要關心其中沒定義的 morphism,我們將基於此集合討論型別 有多大。技術上來說,是指從 terminal object 出發的所有 morphisms(記為 ),這些 morphisms 對應到內建的形式;以邏輯來說是指公理,而在函數式語言裡面,我們最常看到的定義公理的方式就是 data type!換句話說,型別的大小由建構子決定:
- 是 False / Empty type,沒有任何建構子
- 是 Unit type,只有一個建構子
- 是 Bool type,只有兩個建構子
依此類推可以知道有 個單元建構子(即建構子 c 滿足 c : K )的型別 K 可以解釋為 -type,接著 的元素應該有幾個呢?答案是 ,同理我們可以建立 的關係式。
依此可以建立一個簡單的直覺是 c : T 表示 ,而更加複雜的型別如 c : (2 -> T) -> T 就表示 ,建構子的參數表現了型別增長的速度,決定了型別的大小。
一個常見的案例是自然數,我們通常定義 和 兩個建構子來表示自然數 。用 F-algebra 來表示,可以得到 ,從沒有循環參考的角度來看,當前 的大小即取決於上一個 的大小。畫出交換圖就可以了解到從基本點 出發,只有 一個方向可以前進,恰恰就是可數無限大的定義,是以看到這與歸納法的對應時,應當不會太過驚訝。
inductive data type [tt-000J]
inductive data type [tt-000J]
在 dependent type 語言裡面,data type 會變成 inductive data type,引入了更多的限制,而其中跟大小有關的限制就是這裡想要討論的。
Question. 在定義建構子時 c : (T -> T) -> T 有參數 ,試問 有多大?
答案是不知道,因為我們根本還不知道 到底是什麼。
當 定義完畢之後,這個簽名用在函數上倒是沒有問題,因為其大小已經確定,不會遇到自我指涉引發的麻煩。
雖然可以用公理強迫 有 size,但這樣做一來會破壞計算性;二來會顯著的複雜化 termination check。舉例來說,要是容許定義 c,就可以寫出
def foo (t : T) : T := match t with | c f => f t
接著 foo (c foo) 就會陷入無限迴圈,為了要有強正規化,我們希望排除所有這類型的程式,比起一個一個去比對,直接禁止定義 c 這類的建構子可以更簡單的達成目的。Haskell/OCaml 的 data type 則不做此限制,因為它們不需要強正規化,這也是為什麼 dependent type 語言常説其 data type 是 inductive data type,並不輕易省略 inductive 這個詞,因為這樣定義的類型滿足 induction principle。
另外一提,Bauer 談到所有建構子都是為了符合 的形式,有興趣的讀者可以著手證明。此外實現檢查機制時,strictly positive 的遞迴定義可能更適合作為參考。
遞迴 [tt-000G]
遞迴 [tt-000G]
把程式作為 object,而 continuation 作為 morphism,就可以發現尾遞迴完全對應到迴圈這個抽象,兩者都有
- base case 與 break
- induction case 與 next step
這兩個 morphism。從構造的角度來看,還可以說他們跟自然數有對應,上面的簽名恰恰正是 initial 跟 step。
分形遞迴(Tree Recursion) [tt-000K]
分形遞迴(Tree Recursion) [tt-000K]
典型的情況是 fibonacci 數列,展示了前面的型別大小如何與程式相關,常見的程式定義如下
def fib : Nat → Nat | 0 => 1 | 1 => 1 | n+2 => fib n + fib (n+1)
為了抽出計算部分的代數,我們用 inductive type 定義其計算
inductive Fib (a : Type) : Nat → Type where | z : a → Fib a 0 | o : a → Fib a 1 | s : Fib a n → Fib a (n+1) → Fib a (n + 2)
可以看到 induction case 就是 ,所以對應的程式就是兩次呼叫 fib n + fib (n+1) 。當然,因為 fibonacci 還有一個利用矩陣計算的編碼
這個方法對應到 的演算法,因此 fibonacci 不一定要用分形遞迴計算。這件事也告訴了我們代數簽名有時候比我們具體的計算更寬鬆,上面的 inductive type 並未限制如何使用 s,也因此可以摺疊時可能存在更快的計算方式。這也說明了當遇到 c : (T -> T) -> T 一類的建構子時,其對應的計算難以寫出的問題,也就是前面沒辦法定義 的大小的情形。
Parser combinator:文法規則就是組合子的運用 [cs-0009]
Parser combinator:文法規則就是組合子的運用 [cs-0009]
Definition. 左遞迴 [cs-000A]
Definition. 左遞迴 [cs-000A]
左遞迴是我們定義文法的時候會出現的一種形式,比如
翻譯成遞歸下降解析器時會有像下面這樣的程式
def expr : Parsec E := let l <- expr match '+' let r <- expr return E.add l r
這時候 expr 顯然是一個非終止的發散函數,而因為遞迴的原因是運算式的左邊,所以被稱為左遞迴。這樣的 infix 運算形式在文法中很常見,所以我們需要方法來消除文法中的左遞迴。
Definition. Parser combinator [cs-000B]
Definition. Parser combinator [cs-000B]
解析器組合子(parser combinator)最早來自論文 A new top-down parsing algorithm to accommodate ambiguity and left recursion in polynomial time, 在現在的使用中因為不同語言特性跟 parser combinator 指涉的比較像是一種程式方法的情況下,本文中的 parser combinator 是單純指把 parser 跟 higher order function 結合的一種程式方法。這個方案最大的好處就是遞歸下降解析跟程式寫法一一對應,因此相當直覺。
消除左遞迴的方法 [cs-000C]
消除左遞迴的方法 [cs-000C]
現在你知道為什麼我們需要了解遞歸下降解析中消除左遞迴的方式,以下面文法來說
Broken pipe (os error 32)我們可能會將定義改成
Broken pipe (os error 32)這個解法在對應的 parser combinator 中看起來像是
mutual
def term := parse_int <|> parens expr
def expr : Parsec E :=
let l <- term
match '+'
let r <- term
return E.add l r
end擴展到 operator 優先序問題 [cs-000D]
擴展到 operator 優先序問題 [cs-000D]
上面的方法解決了左遞迴問題,但是要是有多個不同優先級的運算形式就會讓文法快速膨脹
Broken pipe (os error 32)這樣單調的修改在文法裡面確實很無聊,不過只要仔細觀察對應的 combinator,就會它們的型別發現這告訴了我們要怎麼利用 higher order function 來解決重複的問題!對 infix 運算形式(左結合)來說,通用的程式是
def infixL (op : Parsec (α → α → α)) (tm : Parsec α) : Parsec α := do let l ← tm match ← tryP op with | .some f => return f l (← tm) | .none => return l
這個 combinator 先解析左邊的 lower tm ,接著要是能夠解析 op 就回傳 op combinator 中存放的函數,否則就回傳左半邊的 tm 結果。使用上就像這樣
mutual
def factor : Parsec Expr
def expr : Parsec Expr :=
factor
|> infixL (parseString "*" *> return Expr.mul)
|> infixL (parseString "+" *> return Expr.add)
end
- 其中
parseString是個假設會進行 whitespace 過濾並 match 目標字串的 combinator Expr.mul跟Expr.add的型別被假設為Expr → Expr → Expr
這裡真正發生的就是使用組合子編碼了文法的層級,其中每個規則都被記錄成匿名函數,我們無需再另外命名。
處理優先度相同的運算子 [cs-000E]
處理優先度相同的運算子 [cs-000E]
因為有些運算子優先級相同,所以我們還需要再修改上面的函數來正確的支援這個概念;而且上面的程式為了避免複雜化,只解析一次 operator 加上 tm 就退出了,會導致實際上 1 + 2 * 3 * 4 這種算式的 * 4 部分沒有被解析。要解決這個問題,我們需要貪婪解析右半邊 op tm 的部分。綜上所述我們得到的程式碼是
def infixL (opList : List (Parsec (α → α → α))) (tm : Parsec α)
: Parsec α := do
let l ← tm
let rs ← many do
for findOp in opList do
match ← tryP findOp with
| .some f => return (f, ← tm)
| .none => continue
fail "cannot match any operator"
return rs.foldl (fun lhs (bin, rhs) => (bin lhs rhs)) l
首先我們有一串 operator 而非一個,其次在右邊能被解析成 op tm 時都進行解析,最後用 foldl 把結果轉換成壓縮後的 α
我希望這次有成功解釋怎麼從規則對應到 parser combinator,所以相似的規則可以抽出相似的 higher order function 來泛化,讓繁瑣的規則命名變成簡單的函數組合。這個技巧當然不會只有在這裡被使用,只要遇到相似形的文法都可以進行類似的抽換,相似的型別簽名可以導出通用化的關鍵。
Appendix. 其他 expression combinator [cs-000F]
Appendix. 其他 expression combinator [cs-000F]
在這裏提到的所有程式都實作在我幫 lean 寫的一個解析器擴充程式庫 https://git.sr.ht/~dannypsnl/parsec-extra 中
右結合的 infix
partial def infixR (opList : List (Parsec (α → α → α))) (tm : Parsec α)
: Parsec α := go #[]
where
go (ls : Array (α × (α → α → α))) : Parsec α := do
let lhs ← tm
for findOp in opList do
match ← tryP findOp with
| .some f => return ← go (ls.push (lhs, f))
| .none => continue
let rhs := lhs
return ls.foldr (fun (lhs, bin) rhs => bin lhs rhs) rhs
prefix op tm
def «prefix» (opList : List $ Parsec (α → α)) (tm : Parsec α)
: Parsec α := do
let mut op := .none
for findOp in opList do
op ← tryP findOp
if op.isSome then break
match op with
| .none => tm
| .some f => return f (← tm)
postfix op tm
def «postfix» (opList : List $ Parsec (α → α)) (tm : Parsec α)
: Parsec α := do
let e ← tm
let mut op := .none
for findOp in opList do
op ← tryP findOp
if op.isSome then break
match op with
| .none => return e
| .some f => return f e什麼是啟動編譯器? (bootstrap compiler) [cs-0001]
什麼是啟動編譯器? (bootstrap compiler) [cs-0001]
當一個語言逐漸成熟,開發者常常會有一個想法就是用自己開發的語言寫這個語言的編譯器,但是這個決策會導致程式庫中有兩套目標一樣但是實現語言不同的編譯器程式。其一是本來的實現,另一個是用語言自身新寫的。一來這樣開發任何新功能的時候都需要寫兩次;二來這會減少可能的參與者人數,因為這下他得要熟悉兩個語言才行!解決這個問題的辦法就是啟動編譯器,通常是一個在多平台上可以直接執行的檔案。
運作原理 [cs-0002]
運作原理 [cs-0002]
約略是下面描述的樣子:
- 語言本身後端的目標語言可以生成這個啟動編譯器,讓我們先用可執行檔簡單理解它,後面再闡述為什麼用普通的可執行檔可能不是一個好主意
- 每次編譯器用到新的特性的時候,都需要更新啟動編譯器檔案並提交進程式庫
- 有了上述準備,就可以在第一次編譯編譯器自身的時候,用啟動編譯器編譯出最佳化過的編譯器執行檔
現在有了最佳化過的編譯器執行檔,就可以正常的使用語言自己對語言自己進行開發了。
現在可以來想一下為什麼是這樣的流程,首先一個程式語言除非被大量作業系統支援(比如 C、Python),否則系統上是不會有這個程式語言的編譯器的!這樣問題就來了:假設有人試圖參與這個編譯器專案,用的平台剛好跟既有開發者都不一樣,請問要由誰提供已經用語言自身編寫的編譯器的編譯器呢?想當然除了一些喪心病狂的作法,是不可能完成這個任務的!所以一個無論如何都已經可以執行的編譯器,哪怕效能比較差,也具有存在的價值。
而語言自身的編譯器用到新功能的時候,也一定要更新啟動編譯器,否則下一輪的新參與者就沒辦法正確的進行初始編譯。
用普通的可執行檔可能不是一個好主意 [cs-0003]
用普通的可執行檔可能不是一個好主意 [cs-0003]
前面提過說啟動編譯器通常是一個在多平台上可以直接執行的檔案,也提過哪怕效能不佳也可以,這兩個理由使得特定平台的可執行檔不是一個好的選擇。 當然,我們也可以選擇維護每個平台的啟動編譯器,chez scheme 就維護了一堆根據不同平台套用組合的二進位檔案做這件事。
回到正題上,啟動編譯器通常不會選擇這麼複雜的方式,而是會生成可以在多平台上執行的檔案。舉例來說,生成 C 或是 Python 這種已經被許多系統廣泛支援的語言,最近 zig 就是使用 wasm 達成這個目標。但這個選擇也不能太過隨便,比如要是語言自己的 type checking 任務很長,生成 Python 就會得到一個大家都不想等它跑完就不玩了的啟動編譯器。而限制太多的語言像是 haskell 或是 rust 可能也不是優秀的選擇,因為你的語言模型很可能跟這些目標語言非常不相配,進而讓編譯過程非常的痛苦。
有了這些概念,我想你已經有能力為自己的語言寫出啟動編譯器了!那麼剩下的篇幅我就可以來寫點 murmur,我覺得這個概念可以進一步推升到選擇一個夠容易編譯出來,也夠容易寫出通用最佳化編譯器的語言來達成。我個人是很看好 wasm,因為它確實容易當目標、最佳化,只可惜現在還有不少重要的功能都沒有定案。llvm 的 bytecode 確實也是一個方案,寫一個把 llvm bytecode 編譯成 executable 的 python 檔案並不困難,但 llvm 的連結性自己就是一個天殺的大麻煩所以這個方案我很少看到有人使用。Java bytecode 則是讓那些本來就預計只在 JRE 生態系內部的語言從一開始就沒有這個問題,微軟的 CLR 也是類似的狀況,缺陷是最後語言受制於 runtime,這個問題會有多大條取決於語言的目的是什麼。
好像是今年最後一天了,祝你不是在今天看到這篇文章的!
polymorphism 的執行期設計 [cs-0000]
polymorphism 的執行期設計 [cs-0000]
在傳統的 ML 或是 Haskell 裡面,有一個型別表現的特別醜陋,就是 data type 表示的 disjoint。 這是因為無論如何,disjoint 就是會需要執行期時有要處理哪個分支的資訊。 因此語言中都設計有 constructor 這麼一個特殊的存在,其中每個 case 都有對應的執行期標籤。 舉例來說,
type bool = false | true
這裡 false 可能就是 0 而 true 是 1。
type nat = z | s of nat
這裡 z 可能就是 0 而 s 是 1 並且接有一個 tuple 放 nat 。
要是這種 disjoint 語義想要完美對應 category theory 的 coproduct,那就需要引入真正的 union type。 要注意到這跟 C 語言的 union 略有不同,C 語言事實上仰賴了開發者完全知道自己在做什麼作為前提, 要求開發者對 union 正確的操作。要是要求 C 語言一樣要能處理不同型別的輸入的話,一樣要放置一個標籤欄位才能解決。 union type 在型別上是很優美,沒有 多餘 的標籤,在 typed/racket 裡面可以記成 (U Integer Boolean String) 之類的。但這個方案遠非毫無缺點,之所以可以這麼做,事實上是因為 racket(以及早期的諸多 functional languages)採用了 universal object 編碼。
Universal object 就是指對每一個執行期的物件,都把型別囊括在內。 這樣一來當然就不需要另外給標籤,因為每個物件本來就都有標籤了。 可想而知,這個方法缺點就是針對需要緊密排列的運用場景效果不佳。 所以 racket 要是需要操作 vector float 這種資料,再怎麼編譯都還是會慢 C 語言一線, 主因就是沒有用最緊密的方式排列資料(多了標籤),相較於 C 沒有利用到當代硬體特性。 但反過來說就沒有 ad-hoc 的編譯難題,因為本來就是需要 runtime 解決的問題就推到 runtime 解決。
那麼可想而知,後來為了適當壓縮物件,ML 跟 Haskell 都走上混合的解決方案。 針對小物件(通常是指小於等於該平台的一個 word 的資料型別)就會盡可能不要包起來,反之就採用 universal object, 在實務上表現也確實不錯。
利用參考等價性質的技巧 [racket-0000]
利用參考等價性質的技巧 [racket-0000]
所謂的使用參考等價性,是指在某些語言裡面,兩個物件是否相同是通過參考而非內容決定的。 舉例來說, racket 裡寫下一個空結構,然後生成一些實例
(struct id ()) (define a (id)) (define b (id)) (define c a)
我們可以用一些 eq? 運算來檢查
> (eq? a b) #f > (eq? a c) #t > (eq? c a) #t > (eq? b c) #f
這樣就可以生成一連串在運行中的程式內唯一的資源標示。
但要小心你用的語言的特性,比如要是我把上面的(struct id ())變成(struct id () #:transparent)並改用equal?運算, racket 就會改用內容而非參考去判定相等。
應用場景
那麼這種技巧可以用在哪些地方呢?首先要注意到這絕對不可以用在序列化上!每次程式重新啟動,同一個宣告都會被重新分配到不同的參考,所以這不能超出程式運行的範疇。 所以合適的用法應該是在程式終止之後就不會再仰賴這個資源唯一性的。
- Racket 自己 Sets of Scopes:在 Matthew Flatt 的 Let's Build a Hygienic Macro Expander 裡,
scope就是一個空結構。 - 型別檢查裡面的自由變數也可以用這個方式生成(這樣我們就不用維護一個 free variables counter)。
- Threading ID: 共時結構要是需要唯一標示的時候,這個技巧就很方便,因為沒有正確運作的記憶體配置器會把物件分配到同一個地方。
這樣的小技巧非常方便,當然也需要注意其限制以及程式語言的實際運作方式。 在使用前最好真的去讀你的語言對參考的處理方式,確保這些程式仰賴的環境假設正確無誤,才不會出現出乎意料的問題。
Algorithm. Strictly positive check [tt-0000]
Algorithm. Strictly positive check [tt-0000]
Why? [tt-0001]
Why? [tt-0001]
strictly positive 是 data type 中對 constructor 的一種特殊要求形成的屬性,這是因為如果一個語言可以定義出不是 strictly positive 的 data type,就可以在 type as logic 中定義出任意邏輯,形成不一致系統。
現在我們知道為什麼我們想知道一個 data type 是不是 strictly positive 了!了解完 strictly positive 的必要性後,我們用例子來理解什麼是不一致的系統,第一個例子是 not-bad :
Example. Not Bad [tt-0004]
Example. Not Bad [tt-0004]
data Bad bad : (Bad → Bottom) → Bad notBad : Bad → Bottom notBad (bad f) = f (bad f) isBad : Bad isBad = bad notBad absurd : Bottom absurd = notBad isBad
Bottom () 本來應該是不可能有任何元素的,即不存在 x 滿足 x : Bottom 這個 judgement,但我們卻成功的建構出 notBad isBad : Bottom。如此一來我們的型別對應到的邏輯系統就有了缺陷。
Example. Loop [tt-0005]
Example. Loop [tt-0005]
現在我們關心一下第二個例子 loop(修改自 Certified Programming with Dependent Types):
data Term abs : (Term → Term) → Term app : Term → Term → Term app (abs f) t = f t w : Term w = abs (λ x → app x x) loop : Term loop = app w w
loop 的計算永遠都不會結束,然而證明器用到的 dependent type theory 卻允許型別依賴 loop 這樣的值,因此就能寫出讓 type checker 無法停止的程式。換句話說,證明器仰賴的性質缺失。事實上 Term 跟 Bad 的問題就是違反了 strictly positive 的性質,或許也有人已經發現了兩者 constructor 型別的相似之處。接下來我們來看為什麼這樣的定義會製造出不一致邏輯。
原理 [tt-0002]
原理 [tt-0002]
首先我們需要理解以下兩條規則
- 蘊含
- 蘊含
根據這兩條規則,我們說 arrow type
- contravariant in (或 varies negatively)
- covariant in (或 varies positively
所以我們稱 為 negative position、 為 positive position
實作 [tt-0003]
實作 [tt-0003]
而 strictly positive 就是說,inductive family 自己不可以出現在 negative position
在 Agda 的文件中也有解釋:任何 constructor 都形如
而每個 都可以不提到 或是形如
不可以等於
文章到這邊告一段落,也解決了我這一年來對證明器實作的最大疑問之一,進一步的解答可以參考 https://cs.stackexchange.com/questions/55646/strict-positivity/55674#55674
Programming 生涯回顧 [2020]
Programming 生涯回顧 [2020]
很久以前就曾經想過要不要寫下這種經驗文,這念頭出現到現在轉眼就過了兩年了 XD。期間真的發生了太多事,現在又到了人生的十字路口所以決定記錄一些東西,希望這篇文章或許能夠啟發一些像我一樣迷惘的人。
大學教育
我接觸程式的時間不是特別早,到了大學才第一次”使用”電腦。那時真的蠻好笑的,我選了這裡的原因是因為我覺得這系名好長好有趣就填在指考志願第一個位置(而我當時也沒有試圖弄懂志願序的用途 XD),亂填的下場就是我爸差點沒氣死。當時幾經考慮,然而最後我還是決定不重考了。因為前進後或許不是一條好的道路,但到時候再後悔就好了,而不前進就必然要耗費一年也未必真的有什麼結果。到了學校,基礎程式課就立刻深深吸引了進了不知道能幹嘛的科系、對未來毫無想法的我。從此我每天從中午 12 點寫程式寫到半夜 3 點,每個禮拜只出現在程式課、書店、圖書館跟房間,搞到很多科都超低空飛過(雖然我也不在意)。印象特別深刻的是當初印出 99 乘法表的作業我硬是搞不懂 loop 的用途,死纏著學長問了 2 小時才寫出來。現在想想,真是佩服學長沒有從此不鳥我呢 XD。大一就在不太懂什麼檔案 IO、資料庫的情況下寫出了人生第一個能夠算是應用程式的程式:課堂的最終測驗,寫出一個運作在 CLI 下的 ATM(當時也不知道什麼是 CLI XD)。大二的資料結構與演算法課程中,小組討論促進了很多有趣的發想跟對演算法的理解(可惜整個科系就只有該門課程的教授這樣上課)。這門課讓我知道很多同學其實都能講出非常有見解的解法,即使他們後來未必會走上開發者這條道路。該課程結束後我跟學長(對,被我纏了 2 小時的那位)更常單獨討論他們當時的專題:為醫療領域優化的搜尋引擎。這個專題重點擺在如何針對特定領域優化搜尋結果,減少搜尋到農場文當然是非常重要的目標之一。由於當時對爬蟲的討論,我開始接觸 Erlang 與 Go 這兩個語言,接著幾個月都在不斷的優化寫好的爬蟲,讓它能夠在最短時間內處理最多的頁面。最後還不小心翻開龍書踏入了 Compiler 的奇妙世界。快樂的時光總是短暫,由於一些經濟因素,我決定休學走上工作的道路。
工作
第一份工作我靠著一個類 python 語言的直譯器說服了老闆為什麼雇用一個高中學歷的人也沒問題 www。現在回想這間公司真的很不錯,只要工作做完就完全不干涉你要做什麼,所以我在這裡寫了不少 Compiler 的程式,還把 redux porting 到 Go 裡面(雖然我到現在也沒弄懂這有什麼意義 XD)。當時朋友都在台北,也因為在家住膩了(結果現在又想回家住了),決定上台北找工作,就在台北待到了現在。剛上台北找工作時有一次很有趣的面試,當時我英文不好(連 Algorithm 都沒聽懂是什麼)、技能樹只往 Compiler 上點,面試官還願意一個一個跟我解釋我的問題在哪裏,最後還鼓勵我有學會的東西都記得很熟練,人真的超好 :),現在還是很感謝他。工作幾年下來,其實慢慢覺得工作帶來的成長不存在了,這也讓我有了想轉換人生跑道的想法,後面會再提。
認識 PLT
在台北工作的兩年多裡慢慢開發著自己的程式語言,隨著得到更多的開發經驗和學習了更多的語言,我逐漸意識到我似乎有什麼根本性的東西根本沒有學到。就像當初我總覺得 Design Pattern 有點怪異、Go 開發者宣稱的簡單似乎不大對一樣的直覺,我發現了 PLT 這個以前從來沒有碰過的領域。從此開始入天坑:lambda calculus -> second order logic -> hindley-milner -> dependent type -> calculus of construction -> MLTT,現在正在讀 cubical type, inductive construction(CIC), HoTT 等。我認為學習 PLT 真的有很大的好處,會逐漸超出單個語言的見解,分解出是什麼讓程式變得好寫而什麼不是。也是對 PLT 的學習讓我終於弄懂為什麼 Go 的設計其實並沒有帶來簡單性、為什麼 Design Pattern 其實沒有必要背誦(甚至沒必要特意學習)。只是隨著了解的深入,我也更不想設計新的程式語言了 www(但又不想廢棄寫很久的專案)。但我不建議對上面的一切沒有興趣還硬讀,cs 有很多事情能做,絕對不只是 PLT。
避免崇拜
我覺得一路走來,最重要的教訓就是不要盲目的崇拜,不只是技術上,在生活中也應該檢視自己是不是做了什麼假設,而不是盲目的用被假設影響後的觀點看待事物。以我個人而言,崇拜過 Go, UNIX 等專案的作者和所謂的 hacker 就是該怎樣,進而導致了很多不良的選擇,例如:硬要用 vim 而不是 IDE、硬要用 CLI 而不是 GUI、明明有現成方案卻要從頭打造整個專案。這不是說用 vim 不對,很多時候我都用 vim。當環境上只有 terminal 或是只是要小改幾行時,我不否認它的編輯能力非常高效,但如果要說起跟 debugger 的整合性、移至定義的精準度、重構的方便度、閱讀其他人的程式碼等等,用 IDE 真的會好很多。關鍵是不要只因為某個看法就放棄對其他可能性的探索。對,就算我推薦 IDE,你還是該學看看 vim 或 emacs,說不準什麼時候就用到了。這也連結到怎麼選擇要學習什麼,只要避免崇拜,就較能以客觀的角度選擇合適的工具。
歸類知識
對知識進行分類是有好處的,記住生命週期長的資訊,而對有生命週期短的資訊不要耗費太多時間。例如說「理解演算法」就比「記住 vim 的 101 個指令」生命週期長的多。這裏,並不只是指事物本身的生命週期,要說起來 vim 活得超久,可能比很多演算法更久,但 vim 是容易過時的,你可能會遇到某些情況 vim 就是沒有 plugin 能用,這時候該做的恐怕不是自己刻個工具而是找替代方案,因為我們通常沒有時間,比起 vim 我更關心我想處理的問題,所以 agda 我用 atom 編輯,因為有方便的套件能用。而演算法就算不是最快的,其發想思路還是有相當的價值。同理對程式語言其實沒有必要花時間掌握語法到能夠「寫出最好的寫法」,因為我們關心的是程式碼解決的什麼問題,不是用什麼程式語言。關鍵是不要為了「非核心」的知識耗費大量心力,若這個「非核心」的知識不是你的興趣也不是你的工作職責。沒錯,如果就是喜歡玩 vim,開發 vim 的 plugin 就是樂趣根源那就去做吧,人類社會之所以能夠運作就是因為每個人是不一樣的。就像 PLT 知識對目標是寫個作業系統的人而言只是「非核心」知識一樣,每個人需要學習的知識都不一樣,所以也沒必要羨慕什麼「大神」,說不準人家還羨慕你能睡好覺,who knows。
下一個階段
雖然我被我講得好像我已經沒有迷惘了似地 XD,但完全不是這樣,我也在考慮去考在職碩士然後出國讀博士走學術這樣的路。人生沒有所謂的成功,有個笑話就說「窮人想有錢,有錢後被權貴欺負,就想著要有權,成官之後整天鬥爭,想想還是平淡的生活好,又成了窮人」,笑話是笑話,但人生沒有最佳解卻是事實,所以就算選了之後後悔也沒關係,需要的只是弄清楚自己接著想做什麼,然後去做。
世界上只有一種真正的英雄主義,那就是在認識生命的真相後,依然熱愛生活。
雖然我說的好像自己什麼都知道了,可惜就算是此時此刻我也搞不清楚我想幹嘛 w,但我還是會繼續學習我有興趣的知識、嘗試看看學術生涯是什麼樣子、體驗不同國家生活的風景。不知不覺就 23 歲,寫了 5 年程式,工作了 3 年,這世上唯一不缺的…大概就是時間不夠的感嘆,希望接下來 3 年也是有趣的人生。
人生不是只有程式碼
最後,人生不是只有程式碼,記得停下來看看那些幫助自己的人,我曾經沒有看清這麼簡單的事實。回憶過往,人生總是在受他人的幫忙,高中時帶給我人生樂趣的數學老師、嘴上抱怨但還是支持我的各種任性決定的父母、大學我整天吃吐司時請我吃飯的同學跟二話不說就借我幾千元的朋友、當初幫我跟老師求情不要當我的同學 www、工作時遇過的同事、在我低潮時聽我講抱怨的廢話的人們,只能再三感謝。這些才是讓我不用擔心,專心開發的支柱,如果有人讀完真的覺得自己沒有這樣的支柱,那也可以寄信給我,雖然我不見得能給什麼建議,保證沒辦法解決問題,但我可以好好聆聽,因為也有曾經願意聽我訴說的陌生人,雖然最後好像跟 programming 根本沒什麼關係 www,但還是希望這篇文章能夠幫助到一些人。話說回來,這部落格真的有讀者?
fun networking: tcp close [programming-0002]
fun networking: tcp close [programming-0002]
Recently we are working on a new feature is about filter packets by HTTP header for our router. This is the concept, we read the header by rules, rules are just some key/value pair. If key missing or value isn't matched, then we drop the packet.
When a connection end, we would remove this connection from allowing pass map.
Anyway, we found a bug is, we use FIN flag to say this packet is the end of the TCP connection, but we know a connection end is a:FIN -> b:ACK -> b:FIN -> a:ACK, a/b is client/server here. So except the first packet, following packets won't pass our router, then connection would never end until timeout, LOL.
Reflection in Go: create a stack[T] [programming-0001]
Reflection in Go: create a stack[T] [programming-0001]
Do you know what can Go's package reflect do?
Whatever you had use it or not. Understanding it is not a bad thing.
A well known thing is Go don't have generic, I'm not going to tell you we have generic, I'm going to tell you some basic trick to have the result like generic.
Take a look on the type Stack
type Stack struct {
stack []interface{}
limitT *reflect.Type
}
limitT is a *reflect.Type, the reason that it's a pointer to reflect.Type rather than reflect.Type is because of we may do not spec it.
We add the Stack by invoke WithT.
func (s *Stack) WithT(v interface{}) *Stack {
t := reflect.TypeOf(v).Elem()
s.limitT = &t
return s
}
Why is reflect.TypeOf(v).Elem()? Because we can't really get an instance that type is an interface! Instead of that, we can get a type is pointer to an interface!
We have a common idiom is using (*SomeInterface)(nil) to get pointer to interface instance.
Now we know that user code can be
type AST interface {
Gen() llvm.Value
}
// main
s := stack.New().WithT((*AST)(nil))
After we do that, user can't push a value do not implement AST. So, how we do that? We do a check at Push
func (s *Stack) Push(element interface{}) {
if s.limitT != nil {
if !reflect.TypeOf(element).Implements(*s.limitT) {
panic(fmt.Sprintf("element must implement type: %s", *s.limitT))
}
}
s.stack = append(s.stack, element)
}
If limitT is not nil, means we do not limit the type, just keep going on. But if we limit the type, we check that element implements limitT or not. If not, we panic the process. Now we have a stack can promise type safe at runtime.
Error is Value [programming-0000]
Error is Value [programming-0000]
I think most Gopher had read error-handling-and-go. Has anyone had watched Go Lift? Let's getting start from Go Lift! The point of Go Lift is: Error is Value. Of course, we know this fact. Do you really understand what that means? In Go Lift, John Cinnamond mentions a trick about wrapping the error by command executor. For example, we create a connection to server:6666 by TCP.
conn := net.Dial("tcp", "server:6666")
Can we? Ah…, No! The correct code is:
conn, err := net.Dial("tcp", "server:6666")
if err != nil {
panic(err)
}
Then we write something through the connection.
nBtye := conn.Write([]byte{`command`})
We want that, but the real code is:
nBtye, err := conn.Write([]byte{`command`})
if err != nil {
panic(err)
}
// using nByte
Next, we read something from server:6666, so we create a reader.
reader := bufio.NewReader(conn)
response := reader.ReadString('\n')
No! We have to handle the error.
response, err := reader.ReadString('\n')
if err != nil {
panic(err)
}
// using response
Howver, the thing hasn't ended yet if we have to rewrite the command if response tells us the command fail? If we are working for a server, we can't just panic? So Go Lift has a solution:
func newSafeConn(network, host string) *safeConn {
conn, err := net.Dial(network, host)
return &safeConn{
err: err,
conn: conn, // It's fine even conn is nil
}
}
type safeConn struct {
err error
conn net.Conn
}
func (conn *safeConn) Write(bs []byte) {
if conn.err != nil {
// if contains error, do nothing
return
}
_, err := conn.Write(bs)
conn.err = err // update error
}
func (conn *safeConn) ReadString(delim byte) string {
if conn.err != nil {
return ""
}
reader := bufio.NewReader(conn.conn)
response, err := reader.ReadString("\n")
conn.err = err
return response
}
Then usage will become
conn := newSafeConn("tcp", "server:6666")
conn.Write([]byte{`command`})
response := conn.ReadString('\n')
if conn.err != nil {
panic(conn.err)
}
// else, do following logic
Can we do much more than this? Yes! We can have an error wrapper for executing the task.
type ErrorWrapper struct {
err error
}
func (wrapper *ErrorWrapper) Then(task func() error) *ErrorWrapper {
if wrapper.err == nil {
wrapper.err = task()
}
return wrapper
}
Then you can put anything you want into it.
w := &ErrorWrapper{err: nil}
var conn net.Conn
w.Then(func() error {
conn, err := net.Dial("tcp", "server:6666")
return err
}).Then(func() error {
_, err := conn.Write([]byte{`command`})
})
Wait! We need to send the connection to next task without an outer scope variable. But how to? Now let's get into reflect magic.
type ErrorWrapper struct {
err error
prevReturns []reflect.Value
}
func NewErrorWrapper(vs ...interface{}) *ErrorWrapper {
args := make([]reflect.Value, 0)
for _, v := range vs {
args = append(args, reflect.ValueOf(v))
}
return &ErrorWrapper{
err: nil,
prevReturns: args,
}
}
func (w *ErrorWrapper) Then(task interface{}) *ErrorWrapper {
rTask := reflect.TypeOf(task)
if rTask.NumOut() < 1 {
panic("at least return error at the end")
}
if w.err == nil {
lenOfReturn := rTask.NumOut()
vTask := reflect.ValueOf(task)
res := vTask.Call(w.prevReturns)
if res[lenOfReturn-1].Interface() != nil {
w.err = res[lenOfReturn-1].Interface().(error)
}
w.prevReturns = res[:lenOfReturn-1]
}
return w
}
func (w *ErrorWrapper) Final(catch func(error)) {
if w.err != nil {
catch(w.err)
}
}
Now, we're coding like:
w := NewErrorWrapper("tcp", "server:6666")
w.Then(func(network, host string) (net.Conn, error) {
conn, err := net.Dial(network, host)
return conn, err
}).Then(func(conn net.Conn) error {
_, err := conn.Write([]byte{`command`})
return err
}).Final(func(e error) {
panic(e)
})Notes [notes]
Notes [notes]
視 natural transformation 為 end [C07X]
視 natural transformation 為 end [C07X]
令 為 category,而 為 functor。則所有 構成的 set of natural transformations 可以視為 end
Theorem. Vaughan (1977) [L3M8]
Theorem. Vaughan (1977) [L3M8]
Rectangles, curves, and Klein bottles, related to Status of the smooth rectangular Peg problem
Every Jordan curve has an inscribed rectangle.
Theorem. Nonexistence of an embedded Klein surface [local-0]
Theorem. Nonexistence of an embedded Klein surface [local-0]
No continuous embedding of the Klein surface into . This is a standard result from algebraic topology. Using Alexander duality to compute homology, we produce a contradiction.
Proof. [local-1]
Proof. [local-1]
Given a Jordan curve , the set of unordered and unequal pairs of points in , denoted , is an open Möbius band. Because every unequal unordered pair of points in the circle determines a unique point in : Take the two tangent lines to the circle at these points and intersect them.
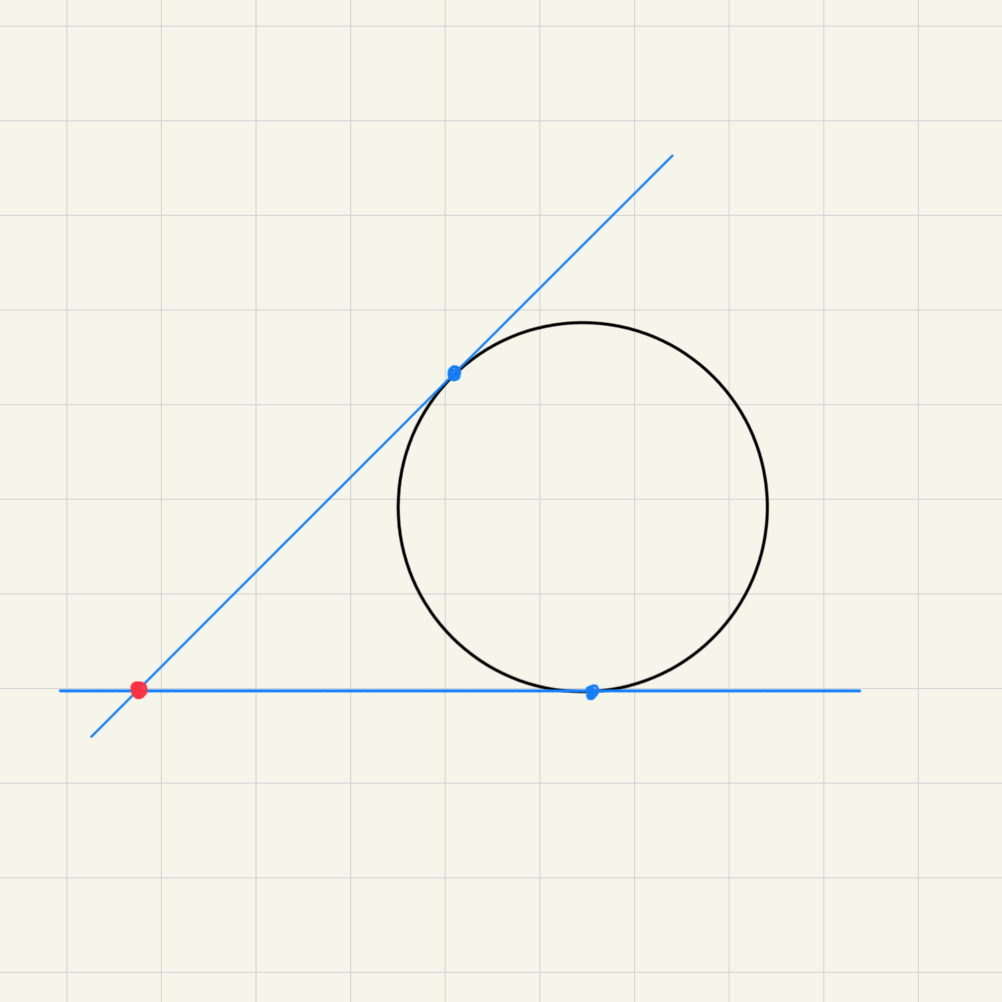
If tangent lines are parallel, than it indicates the infinite point of :
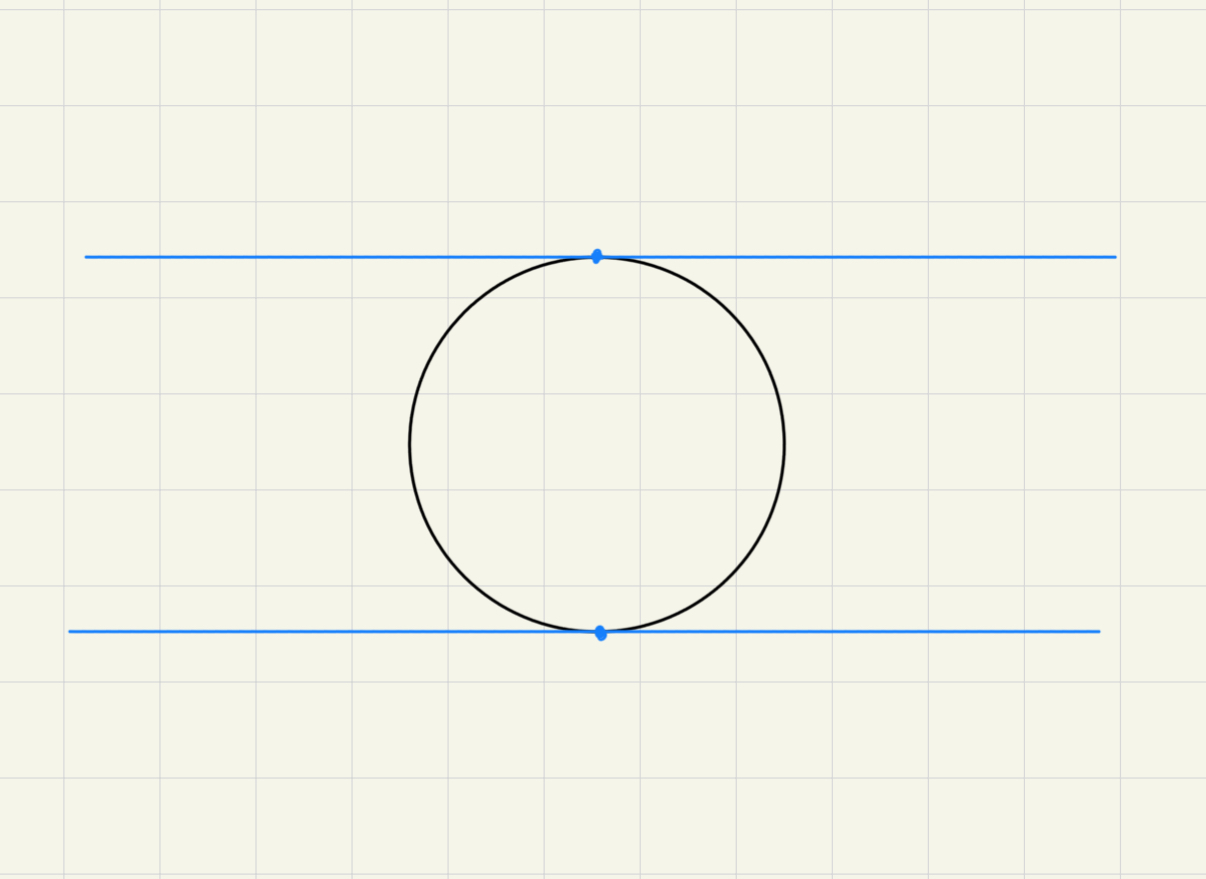
Therefore, are the points of the complement of the closed unit disk in the projective plane, hence an open Möbius band.
Consider a map defined by
Geometrically, maps the ordered pair to a point encoding the midpoint of the segment (2D) and the length of the segment (1D).
If , then these four points form an inscribed rectangle. Hence we just need to prove that the map is not injective!
Consider where reflects the shape in the XY-plane. This is a Klein surface by gluing two Möbius strips at their boundary.
If is injective, then can be embedded into , which contradicts the theorem that nonexistence of an embedded Klein surface into .
Model mapping TT to untyped LC [ag-000Y]
Model mapping TT to untyped LC [ag-000Y]
{-# OPTIONS --without-K #-} open import MLTT.Spartan hiding (Π; zero; succ) open import UF.FunExt open import ag-000V open import ag-000W module ag-000Y (fe : Fun-Ext) where
A model mapping TT to untyped lambda calculus.
module LC-TT {𝓤 𝓥 : Universe} (l : LC {𝓥}) where open LC open TT open TT-sorts open TT-ctors ex-sorts : TT-sorts {𝓤} {𝓥} ex-sorts .Ty = 𝟙 ex-sorts .Tm _ = l .Λ ex-ctors : TT-ctors ex-sorts ex-ctors .Π A B = ⋆ ex-ctors .lam f = l .lambda f ex-ctors .app f x = l .apply f x ex-ctors .lam-app = l .η _ ex-ctors .app-lam {a}{b}{f} = (λ x → l .apply (l .lambda f) x) =⟨ dfunext fe (λ x → l .β f x) ⟩ (λ x → f x) =⟨ refl ⟩ f ∎ ex-ctors .U = ⋆ ex-ctors .El _ = ⋆ ex-ctors .Nat = ⋆ ex-ctors .zero = zeroΛ l ex-ctors .succ x = succΛ l x ex-ctors .elim-Nat X ze su n = recΛ l ze su n ex-ctors .elim-Nat-zero = recΛβ-zero l ex-ctors .elim-Nat-succ = recΛβ-succ l ex : TT {𝓤} {𝓥} ex .sorts = ex-sorts ex .ctors = ex-ctors
SOGAT of type theory with -types, a Tarski universe, and natural numbers [ag-000W]
SOGAT of type theory with -types, a Tarski universe, and natural numbers [ag-000W]
Learn from https://github.com/kontheocharis/erasure-agda
{-# OPTIONS --without-K --confluence-check #-} module ag-000W where open import MLTT.Spartan hiding (Π; zero; succ) coe : {X X' : 𝓤 ̇ } → X = X' → X → X' coe = transport id
TT 要用的 sorts,以及如果 Type 相等,可以轉換 term 用的 helper
coeTm
record TT-sorts : (𝓤 ⊔ 𝓥)⁺ ̇ where field Ty : 𝓤 ̇ Tm : Ty → 𝓥 ̇ coeTm : ∀ {A B : Ty} → A = B → Tm A → Tm B coeTm p a = coe (ap Tm p) a
TT 的 SOGAT
module _ (sorts : TT-sorts {𝓤} {𝓥}) where open TT-sorts sorts private variable A B C : Ty X Y Z : Tm _ → Ty t u v : Tm _ f g h : (a : Tm _) → Tm _ eq : _ = _ record TT-ctors : (𝓤 ⊔ 𝓥)⁺ ̇ where field -- Pi types Π : (A : Ty) → (Tm A → Ty) → Ty lam : ((a : Tm A) → Tm (X a)) → Tm (Π A X) app : Tm (Π A X) → (a : Tm A) → Tm (X a) lam-app : lam (app t) = t app-lam : app (lam f) = f -- Universe U : Ty El : Tm U → Ty -- Natural numbers Nat : Ty zero : Tm Nat succ : Tm Nat → Tm Nat elim-Nat : (X : Tm Nat → Ty) → (Tm (X zero)) → ((n : Tm Nat) → Tm (X n) → Tm (X (succ n))) → (n : Tm Nat) → Tm (X n) -- Computation for elim-Nat elim-Nat-zero : ∀ {mz ms} → elim-Nat X mz ms zero = mz elim-Nat-succ : ∀ {mz ms n} → elim-Nat X mz ms (succ n) = ms n (elim-Nat X mz ms n) record TT : (𝓤 ⊔ 𝓥)⁺ ̇ where field sorts : TT-sorts {𝓤} {𝓥} open TT-sorts sorts public field ctors : TT-ctors sorts open TT-ctors ctors public
Definition. Riemann curvature tensor [B2D1]
Definition. Riemann curvature tensor [B2D1]
The curvature of a Riemannian manifold is a tensor
where are vector fields, is the Levi-Civita connection of the metric (see Lectures on the Geometry of Manifolds Proposition 4.1.9.).
In local coordinates we have
In terms of the Christoffel symbols we have
Lowering the indices we have a new tensor
Theorem. The Hairy Ball Theorem [DRE0]
Theorem. The Hairy Ball Theorem [DRE0]
用 constant vector field on plane 然後拉回 的定義方法很妙。
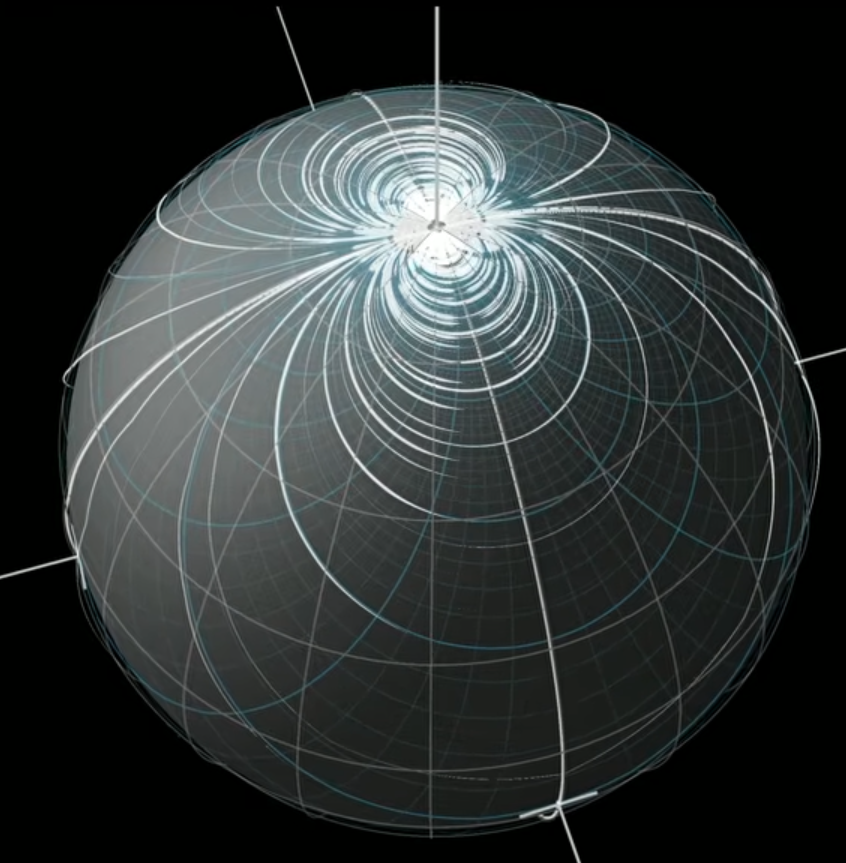
定理的證明是用 Flux 不變,但如果有處處非零的連續向量場,就可以讓 Flux 改變,矛盾。因此這樣的向量場不可能存在。
3-sphere (群 ) 跟 [JRT2]
3-sphere (群 ) 跟 [JRT2]
用 quotient 掉 antipodal points 會得到 Real projective space 。
Proposition. is not simple [local-1]
Proposition. is not simple [local-1]
Proof. [local-0]
Proof. [local-0]
因為 是 的 normal subgroup: 跟 for all 都還是屬於 。
而 nontrivial,有 nontrivial normal subgroup 的群 not simple
是群 :The group of rotations of 。 is simple 所以跟 不是同一個群
作為一個群可以視為 2x2 複數矩陣的群,元素為
這又稱為 The special unitary group 。
Definition. Hopf bundle [5A3M]
Definition. Hopf bundle [5A3M]
Identify the unit odd dimensional sphere with the submanifold
an -action on given by
The complex projective space is isomorphic to , the group corresponds to . This quotient map is a principal bundle called Hopf bundle.
- by definition of
- Use (because , these describe all points in the projective space). The map defined by then
SOGAT of untyped lambda calculus [ag-000V]
SOGAT of untyped lambda calculus [ag-000V]
{-# OPTIONS --safe --without-K #-} open import MLTT.Spartan hiding (id) open import ag-0005 module ag-000V where
SOGAT of untyped lambda calculus.
record LC : 𝓤 ⁺ ̇ where field Λ : 𝓤 ̇ lambda : (f : Λ → Λ) → Λ apply : Λ → Λ → Λ β : ∀ f x → apply (lambda f) x = f x η : ∀ f → lambda (λ x → apply f x) = f _$_ : Λ → Λ → Λ x $ y = apply x y infixl 30 _$_ syntax lambda (λ x → t) = ƛ x ⇒ t zeroΛ : Λ zeroΛ = ƛ z ⇒ ƛ s ⇒ z succΛ : Λ → Λ succΛ n = ƛ z ⇒ ƛ s ⇒ (s $ n $ (n $ z $ s)) id : Λ id = ƛ x ⇒ x recΛ : Λ → (Λ → Λ → Λ) → Λ → Λ recΛ zr su n = n $ zr $ (ƛ k ⇒ ƛ sk ⇒ su k sk) recΛβ-zero : ∀ {zr su} → recΛ zr su zeroΛ = zr recΛβ-zero {zr} {su} = (ap (_$ (ƛ k ⇒ ƛ sk ⇒ su k sk)) (β (λ z → ƛ s ⇒ z) zr)) ∙ (β (λ _ → zr) (ƛ k ⇒ ƛ sk ⇒ su k sk)) recΛβ-succ : ∀ {zr su n} → recΛ zr su (succΛ n) = su n (recΛ zr su n) recΛβ-succ {zr} {su} {n} = (ap (_$ (ƛ k ⇒ ƛ sk ⇒ su k sk)) (β (λ z → ƛ s ⇒ (s $ n $ (n $ z $ s))) zr)) ∙ (β (λ s → s $ n $ (n $ zr $ s)) (ƛ k ⇒ ƛ sk ⇒ su k sk)) ∙ (ap (_$ (n $ zr $ (ƛ k ⇒ ƛ sk ⇒ su k sk))) (β (λ k → ƛ sk ⇒ su k sk) n)) ∙ (β (λ sk → su n sk) (n $ zr $ (ƛ k ⇒ ƛ sk ⇒ su k sk))) embed-nat : ℕ → Λ embed-nat 0 = zeroΛ embed-nat (succ x) = succΛ (embed-nat x)
Lambda calculus (Second-order algebraic theories) universe polymorphic extended.
代數幾何:視 -element 為函數 [WYCP]
代數幾何:視 -element 為函數 [WYCP]
在 manifold 上我們可以定義 。在代數幾何裡面我們想要抽象並仿造這個結構,所以若 為一點(亦同時是 prime ideal),residue field at point 定義為 the field of fractions of the quotient ring
那麼,每個 取 使 可以被視為一個「函數」,不過在不同點 的 codomain 都不同。構造即取 再取 。
Status of the smooth rectangular Peg problem [VEYQ]
Status of the smooth rectangular Peg problem [VEYQ]
https://www.math.columbia.edu/~ums/Peg%20problem%20-%20slides.pdf
- Emch (1913) solved the problem for smooth convex curves. (Proof uses configuration spaces and homology.)
- Schnirelman (1929) solved it for any smooth Jordan curve.
Theorem. Vaughan (1977) [local-0]
Theorem. Vaughan (1977) [local-0]
Every continuous Jordan curve contains four points forming the vertices of some rectangle. This is what 3b1b did, see video here.
Theorem. Greene-Lobb (2020) [local-1]
Theorem. Greene-Lobb (2020) [local-1]
Given a smooth Jordan curve and a rectangle in the plane, then contain four points forming the vertices of a rectangle similar to R.
Theorem. Barr's theorem [KGRZ]
Theorem. Barr's theorem [KGRZ]
If is a Grothendieck topos, then there is a surjective geometric morphism
where satisfies the axiom of choice.
presheaves exponential 同構的推導 [21ME]
presheaves exponential 同構的推導 [21ME]
Topos Theory 的 1.12
令 為 category 的 presheaves,那麼
Proof. [local-0]
Proof. [local-0]
- 用 Presheaves are colimits of representables 改寫
- Contravariant 用到的是 Hom-functor preserves limits
Proposition. Hom-functor preserves limits [math-TGEI]
Proposition. Hom-functor preserves limits [math-TGEI]
This is a very useful property of hom-functor.
Let be a category, then its hom-functor can be wrote as
If the limit exists in , then for all there is a natural isomorphism
If the colimit exists in , then for all there is a natural isomorphism
See nLab for more details.
Definition. Holonomy [math-L2W1]
Definition. Holonomy [math-L2W1]
Let be a vector bundle with a connection . The holonomy of along a closed path is the parallel transport along .
Definition. Parallel transport [math-XU4I]
Definition. Parallel transport [math-XU4I]
Let be a vector bundle with a connection . For any smooth path we will define a linear isomorphism called the parallel transport along .
The construction [local-0]
The construction [local-0]
More precisely, we construct a family of linear isomorphisms:
for all . Consider arbitrary , let be a vector, then define , we know . What we are searching is a "constant" path, in the sense that derivative is , hence we want
so this suggests a way of defining : For any and any , define as the value at of the solution of the initial value problem:
And this is a system of linear ordinary differential equations in disguise.
Definition. Covariant Derivative (Linear Connection) [math-HCIJ]
Definition. Covariant Derivative (Linear Connection) [math-HCIJ]
Let be a vector bundle. A covariant derivative on is a -linear map
such that, for all and all , we have
where denotes the space of smooth sections of over .
Remind that
Therefore, has a more traditional view
When a map is an equivalence? [RNNM]
When a map is an equivalence? [RNNM]
For a given function , the following are two correct definitions of f is an equivalence.
Defintion. Voevodsky's [ag-000T]
Defintion. Voevodsky's [ag-000T]
is an equivalence if its fibers are contractible (or singletons): For every , the type
fiber : {X : 𝓤 ̇ } {Y : 𝓥 ̇ } → (X → Y) → Y → 𝓤 ⊔ 𝓥 ̇ fiber f y = Σ x ꞉ domain f , f x = y
has the property that there is a distinguished element σ0 : fiber f y such that σ = σ0 for all σ : fiber f y.
is-equiv : {X : 𝓤 ̇ } {Y : 𝓥 ̇ } → (f : X → Y) → 𝓤 ⊔ 𝓥 ̇ is-equiv f = ∀ (y : codomain f) → Σ σ₀ ꞉ fiber f y , ∀ (σ : fiber f y) → σ = σ₀
Defintion. Joyal's [ag-000U]
Defintion. Joyal's [ag-000U]
is an equivalence if it has a section and also has a retraction:
{-# OPTIONS --safe --without-K #-} module ag-000U where open import MLTT.Spartan open import UF.Base open import UF.Sets open import UF.Sets-Properties
is-equiv : {X : 𝓤 ̇ } {Y : 𝓥 ̇ } → (f : X → Y) → 𝓤 ⊔ 𝓥 ̇ is-equiv f = (Σ s ꞉ (codomain f → domain f) , f ∘ s ∼ id) × (Σ r ꞉ (codomain f → domain f) , r ∘ f ∼ id)
Of course, the second post in thread is more important, there is a wrong definition, and Escardo shows why it's wrong.
什麼是量子幾何 [FWA9]
什麼是量子幾何 [FWA9]
Why , A Four Dimensional Proof [E963]
Why , A Four Dimensional Proof [E963]
JIT: Write XOR Execute policy [UIC7]
JIT: Write XOR Execute policy [UIC7]
所謂的 W^X (Write XOR Execute) policy 是指不要讓記憶體同時是 PROT_WRITE 跟 PROT_EXEC,所以正確的配置方式是(參見 mmap)
- 先設定成
PROT_READ | PROT_WRITE - 等寫完指令再改成
PROT_READ | PROT_EXEC(像是用mprotecthttps://man7.org/linux/man-pages/man2/mprotect.2.html)
然後才能真的執行這段程式。
Corollary. About Boolean ring [math-HS0H]
Corollary. About Boolean ring [math-HS0H]
Let be a Boolean ring (see nLab) and .
Tool. Unsure Calculator [VIPY]
Tool. Unsure Calculator [VIPY]
Theorem. The field of fractions is a torsion-free module [math-3E35]
Theorem. The field of fractions is a torsion-free module [math-3E35]
Let be an integral domain, and is the field of fractions of . Then is a torsion-free -module (see The Stacks project tag/0549).
Proof. [local-0]
Proof. [local-0]
We want to show that the only torsion element of is . Every element of has the form where , now suppose is a torsion. Then there exists a such that
which leads
in an integral domain, this leads or , but by definition, hence . Which means is , be torsion is be zero in , is a torsion-free -module.
Theorem. Premanifold 為 Hausdorff 的等價條件 [math-T4B3]
Theorem. Premanifold 為 Hausdorff 的等價條件 [math-T4B3]
令 為一個 premanifold(field 為 或是 )。則以下條件等價:
- 為 Hausdorff 空間
- 對於 中任意相異兩點 (),存在開集 使得 ,且在 中,存在函數 使得
Proof. [local-0]
Proof. [local-0]
(2) ⇒ (1):設 為相異兩點。由條件 (2),存在開集 使得 ,且存在 使得 。
令 。因為 為 smooth 函數,存在 的開鄰域 使所有 ,有 。
同理,存在 的開鄰域 使得對所有 ,有 。於是我們知道 ,因為如果存在 ,則:
為矛盾,也就是說不存在這種 。因此 為 Hausdorff 空間。
(1) ⇒ (2):設 為相異兩點。因為 為 Hausdorff 空間,存在不相交的開鄰域 和 使得 。
因為 為 premanifold,存在 open cover 使得每個 與某個 local ringed space 同構。因此存在 和 使得 且 。
考慮開集 和 。因為 ,我們有 。
取 的開鄰域 及函數 使得 (此函數對應於 stalk 的 maximal ideal 中的元素)。同理,取 的開鄰域 及函數 使得 (對應於 stalk 中不在 maximal ideal 的元素)。
令 ,則 為開集且 。因 與 不相交,可定義函數 ,在 上取 ,在 上取 。於是 而 , 與 滿足條件 (2)。
NOTE: Explicit Weakening [ag-000S]
NOTE: Explicit Weakening [ag-000S]
在 Substitution Without Copy and Paste 結尾也有提過這篇,就來稍微看一下。
Explicit Weakening
{-# OPTIONS --rewriting --no-level-universe #-} module ag-000S where open import MLTT.Spartan hiding (Type; id) {-# BUILTIN REWRITE _=_ #-} cong₂ : ∀ {A B C : 𝓤 ̇ } (f : A → B → C) {x y u v} → x = y → u = v → f x u = f y v cong₂ f refl refl = refl
data Type : 𝓤₀ ̇ where base : Type _⇒_ : Type → Type → Type infixr 7 _⇒_ variable A B C : Type data Con : 𝓤₀ ̇ where ∅ : Con _▷_ : Con → Type → Con infixl 5 _▷_ variable Γ Δ Θ Ξ : Con data _⊢_ : Con → Type → 𝓤₀ ̇ where • : Γ ▷ A ⊢ A _↑ : (M : Γ ⊢ B) ------------ → Γ ▷ A ⊢ B ƛ_ : (N : Γ ▷ A ⊢ B) → Γ ⊢ A ⇒ B _·_ : (L : Γ ⊢ A ⇒ B) (M : Γ ⊢ A) ----------------------------- → Γ ⊢ B infix 5 ƛ_ infix 4 _⊢_ infixl 7 _·_ variable L M N P Q : Γ ⊢ A data _⊨_ : Con → Con → 𝓤₀ ̇ where id : Δ ⊨ Δ _↑ : (σ : Γ ⊨ Δ) → Γ ▷ A ⊨ Δ _▷_ : (σ : Γ ⊨ Δ) (M : Γ ⊢ A) ------------ → Γ ⊨ Δ ▷ A infix 4 _⊨_ infix 8 _↑ variable σ τ υ : Γ ⊨ Δ pattern △ = _ ▷ _
Instantiation
_[_] : (M : Δ ⊢ A) (σ : Γ ⊨ Δ) → Γ ⊢ A M [ id ] = M M [ σ ↑ ] = (M [ σ ]) ↑ • [ σ ▷ P ] = P (M ↑) [ σ ▷ P ] = M [ σ ] (ƛ M) [ σ @ △ ] = ƛ (M [ σ ↑ ▷ • ]) (L · M) [ σ @ △ ] = L [ σ ] · (M [ σ ]) _⨟_ : (σ : Θ ⊨ Δ) (τ : Γ ⊨ Θ) → Γ ⊨ Δ σ ⨟ id = σ σ ⨟ (τ ↑) = (σ ⨟ τ) ↑ id ⨟ τ @ △ = τ (σ ↑) ⨟ (τ ▷ Q) = σ ⨟ τ (σ ▷ P) ⨟ τ @ △ = (σ ⨟ τ) ▷ (P [ τ ]) infixl 5 _⨟_ [][] : (M : Δ ⊢ A) (σ : Θ ⊨ Δ) (τ : Γ ⊨ Θ) → M [ σ ] [ τ ] = M [ σ ⨟ τ ] [][] M σ id = refl [][] M σ (τ ↑) = ap _↑ ([][] M σ τ) [][] M id (τ ▷ M₁) = refl [][] M (σ ↑) (τ ▷ M₁) = [][] M σ τ [][] • (σ ▷ P) τ@△ = refl [][] (M ↑) (σ ▷ P) τ@△ = [][] M σ τ [][] (ƛ N) σ@△ τ@△ = ap ƛ_ ([][] N (σ ↑ ▷ •) (τ ↑ ▷ •)) [][] (L · M) σ@△ τ@△ = cong₂ _·_ ([][] L σ τ) ([][] M σ τ) {-# REWRITE [][] #-}
Left identity
left-id : (τ : Γ ⊨ Δ) → id ⨟ τ = τ left-id id = refl left-id (τ ↑) = ap _↑ (left-id τ) left-id (τ ▷ Q) = refl {-# REWRITE left-id #-}
Associative
assoc : (σ : Θ ⊨ Δ) (τ : Ξ ⊨ Θ) (υ : Γ ⊨ Ξ) → (σ ⨟ τ) ⨟ υ = σ ⨟ (τ ⨟ υ) assoc σ τ id = refl assoc σ τ (υ ↑) = ap _↑ (assoc σ τ υ) assoc σ id (υ ▷ M) = refl assoc σ (τ ↑) (υ ▷ M) = assoc σ τ υ assoc id (τ ▷ M₁) (υ ▷ M) = refl assoc (σ ↑) (τ ▷ M₁) (υ ▷ M) = assoc σ τ (υ ▷ M) assoc (σ ▷ M₂) (τ ▷ M₁) (υ ▷ M) = cong₂ _▷_ (assoc σ (τ ▷ M₁) (υ ▷ M)) refl {-# REWRITE assoc #-}
下面的案例是本來在 PLFA 中不好做出來,但用這套就很簡單的問題
_[_]₀ : (N : Γ ▷ A ⊢ B) (M : Γ ⊢ A) ------------ → Γ ⊢ B N [ M ]₀ = N [ id ▷ M ] _[_]₁ : (N : Γ ▷ A ▷ B ⊢ C) (M : Γ ⊢ A) ------------ → Γ ▷ B ⊢ C N [ M ]₁ = N [ (id ▷ M) ↑ ▷ • ] double-subst : N [ M ]₁ [ L ]₀ = N [ L ↑ ]₀ [ M ]₀ double-subst = refl commute-subst : N [ M ]₀ [ L ]₀ = N [ L ]₁ [ M [ L ]₀ ]₀ commute-subst = refl
最後也有談到缺點是 identifying when terms are equivalent may become more difficult,但我沒有試這是什麼清況。
NOTE: Substitution Without Copy and Paste [tt-IHCF]
NOTE: Substitution Without Copy and Paste [tt-IHCF]
Substitution Without Copy and Paste
The copy-and-paste approach [ag-000M]
The copy-and-paste approach [ag-000M]
{-# OPTIONS --safe --without-K #-} module ag-000M where open import MLTT.Spartan
類型跟 context
data Ty : 𝓤₀ ̇ where base : Ty _⇒_ : Ty → Ty → Ty infixl 50 _⇒_ data Con : 𝓤₀ ̇ where ◇ : Con _▷_ : Con → Ty → Con infixl 40 _▷_
- 等一下用的變數
- de Bruijn variables
- terms
variable Γ Δ Ξ : Con A B C : Ty data _∋_ : Con → Ty → 𝓤₀ ̇ where here : Γ ▷ A ∋ A there : Γ ∋ A → (B : Ty) ------------------ → Γ ▷ B ∋ A infixl 30 _∋_ data _⊢_ : Con → Ty → 𝓤₀ ̇ where -- embeds variables in λ-terms `_ : Γ ∋ A → Γ ⊢ A -- application t · u _·_ : Γ ⊢ A ⇒ B → Γ ⊢ A → Γ ⊢ B ƛ_ : Γ ▷ A ⊢ B → Γ ⊢ A ⇒ B infixl 20 _⊢_ infixl 60 `_ infixl 50 _·_ infixl 40 ƛ_
substitution 定義成
data _⊩_ : Con → Con → 𝓤₀ ̇ where ε : Γ ⊩ ◇ _,_ : Γ ⊩ Δ → Γ ⊢ A → Γ ⊩ Δ ▷ A
現在要定義 substitution 在 terms 跟 variables 上的作用:
_v[_] : Δ ∋ A → Γ ⊩ Δ → Γ ⊢ A here v[ ts , t ] = t there i B v[ ts , t ] = i v[ ts ] data _⊩v_ : Con → Con → 𝓤₀ ̇ where ε : Γ ⊩v ◇ _,_ : Γ ⊩v Δ → Γ ∋ A → Γ ⊩v Δ ▷ A _v[_]v : Γ ∋ A → Δ ⊩v Γ → Δ ∋ A here v[ is , i ]v = i there i B v[ is , j ]v = i v[ is ]v _⁺v_ : Γ ⊩v Δ → (A : Ty) → Γ ▷ A ⊩v Δ ε ⁺v A = ε (is , i) ⁺v A = (is ⁺v A) , there i A _↑v_ : Γ ⊩v Δ → (A : Ty) → Γ ▷ A ⊩v Δ ▷ A is ↑v A = (is ⁺v A) , here _[_]v : Γ ⊢ A → Δ ⊩v Γ → Δ ⊢ A (` i) [ is ]v = ` (i v[ is ]v) (t · u) [ is ]v = (t [ is ]v) · (u [ is ]v) (ƛ t) [ is ]v = ƛ (t [ is ↑v _ ]v) idv : Γ ⊩v Γ idv {Γ = ◇} = ε idv {Γ = Γ ▷ A} = idv ↑v A
為了定義下面的 suc-tm,需要定義上面大量的類似結構
Γ ⊩v Δ
_⁺_ : Γ ⊩ Δ → (A : Ty) → Γ ▷ A ⊩ Δ ε ⁺ A = ε (ts , t) ⁺ A = (ts ⁺ A) , suc-tm t A where suc-tm : Γ ⊢ B → (A : Ty) → Γ ▷ A ⊢ B suc-tm t A = t [ idv ⁺v A ]v _↑_ : Γ ⊩ Δ → (A : Ty) → Γ ▷ A ⊩ Δ ▷ A ts ↑ A = ts ⁺ A , ` here _[_] : Γ ⊢ A → Δ ⊩ Γ → Δ ⊢ A (` i) [ ts ] = i v[ ts ] (t · u) [ ts ] = (t [ ts ]) · (u [ ts ]) (ƛ t) [ ts ] = ƛ (t [ ts ↑ _ ])
所以為了避免這些重複,方法要改成:
Substituion without copy and paste 的提議 [ag-000N]
Substituion without copy and paste 的提議 [ag-000N]
{-# OPTIONS --safe --without-K #-} module ag-000N where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) variable Γ Δ Ξ : Con A B C : Ty
引入 Sort 區分 variable 跟 term 的情況
mutual data Sort : 𝓤₀ ̇ where V : Sort T>V : (s : Sort) → IsV s → Sort data IsV : Sort → 𝓤₀ ̇ where isV : IsV V pattern T = T>V V isV variable q r s : Sort
這樣就可以把 variables 跟 terms 定義到一起,用 s 區分
Γ ⊢[ s ] A 是 variable 還是 term
data _⊢[_]_ : Con → Sort → Ty → 𝓤₀ ̇ where here : Γ ▷ A ⊢[ V ] A there : Γ ⊢[ V ] A → (B : Ty) → Γ ▷ B ⊢[ V ] A `_ : Γ ⊢[ V ] A → Γ ⊢[ T ] A _·_ : Γ ⊢[ T ] A ⇒ B → Γ ⊢[ T ] A → Γ ⊢[ T ] B ƛ_ : Γ ▷ A ⊢[ T ] B → Γ ⊢[ T ] A ⇒ B variable x y z : Γ ⊢[ q ] A
substitution 現在定義成
data _⊩[_]_ : Con → Sort → Con → 𝓤₀ ̇ where ε : Γ ⊩[ q ] ◇ _,_ : Γ ⊩[ q ] Δ → Γ ⊢[ q ] A → Γ ⊩[ q ] Δ ▷ A variable xs ys zs : Δ ⊩[ q ] Γ
現在需要考慮 sort 之間的關係,這些 lemma 有助於簡化後面的證明
data _⊑_ : Sort → Sort → Set where rfl : s ⊑ s v⊑t : V ⊑ T _⊔_ : Sort → Sort → Sort V ⊔ r = r T ⊔ r = T
一些輔助用的 REWRITE [ag-000O]
一些輔助用的 REWRITE [ag-000O]
{-# OPTIONS --without-K --rewriting #-} module ag-000O where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N {-# BUILTIN REWRITE _=_ #-}
這邊的定義很繁瑣但只是單純攤開 V、T
就能證明,並不是很重要。重點在最後用 REWRITE
避免後續需要證明一些麻煩的情況
⊑t : s ⊑ T ⊑t {V} = v⊑t ⊑t {T} = rfl v⊑ : V ⊑ s v⊑ {V} = rfl v⊑ {T} = v⊑t ⊑q⊔ : q ⊑ (q ⊔ r) ⊑q⊔ {V}{V} = rfl ⊑q⊔ {V}{T} = v⊑t ⊑q⊔ {T}{V} = rfl ⊑q⊔ {T}{T} = rfl ⊔⊔ : q ⊔ (r ⊔ s) = (q ⊔ r) ⊔ s ⊔⊔ {V}{V}{V} = refl ⊔⊔ {V}{V}{T} = refl ⊔⊔ {V}{T}{V} = refl ⊔⊔ {V}{T}{T} = refl ⊔⊔ {T}{V}{V} = refl ⊔⊔ {T}{V}{T} = refl ⊔⊔ {T}{T}{V} = refl ⊔⊔ {T}{T}{T} = refl ⊔v : q ⊔ V = q ⊔v {V} = refl ⊔v {T} = refl ⊔t : q ⊔ T = T ⊔t {V} = refl ⊔t {T} = refl ⊑⊔r : r ⊑ (q ⊔ r) ⊑⊔r {V}{V} = rfl ⊑⊔r {V}{T} = v⊑t ⊑⊔r {T}{V} = rfl ⊑⊔r {T}{T} = rfl ⊔-self : q ⊔ q = q ⊔-self {V} = refl ⊔-self {T} = refl {-# REWRITE ⊔⊔ ⊔v ⊔t ⊔-self #-}
substitution 的組合 [ag-000P]
substitution 的組合 [ag-000P]
{-# OPTIONS --without-K --rewriting #-} module ag-000P where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N open import ag-000O
這裡的目的是定義 ⊑ relation 對 term 的影響,以及定義
substitution 的結合 ◦
tm⊑ : q ⊑ s → Γ ⊢[ q ] A → Γ ⊢[ s ] A tm⊑ rfl x = x tm⊑ v⊑t i = ` i here[_] : (q : Sort) → Γ ▷ A ⊢[ q ] A here[ V ] = here here[ T ] = ` here mutual _[_] : Γ ⊢[ q ] A → Δ ⊩[ r ] Γ → Δ ⊢[ q ⊔ r ] A here [ xs , x ] = x there i _ [ xs , x ] = i [ xs ] (` i) [ xs ] = tm⊑ ⊑t (i [ xs ]) (t · u) [ xs ] = (t [ xs ]) · (u [ xs ]) (ƛ t) [ xs ] = ƛ (t [ xs ↑ _ ]) id-poly : (q : Sort) → Γ ⊩[ q ] Γ id-poly {Γ = ◇} q = ε id-poly {Γ = Γ ▷ A} q = id-poly q ↑ A id : Γ ⊩[ V ] Γ id = id-poly V {-# INLINE id #-} there[_] : (q : Sort) → Γ ⊢[ q ] B → (A : Ty) → Γ ▷ A ⊢[ q ] B there[ V ] i A = there i A there[ T ] t A = t [ id ⁺ A ] _⁺_ : Γ ⊩[ q ] Δ → (A : Ty) → Γ ▷ A ⊩[ q ] Δ ε ⁺ A = ε (ts , t) ⁺ A = (ts ⁺ A) , there[ _ ] t A _↑_ : Γ ⊩[ q ] Δ → (A : Ty) → Γ ▷ A ⊩[ q ] Δ ▷ A ts ↑ A = ts ⁺ A , here[ _ ] infixl 70 _⁺_ _◦_ : Γ ⊩[ q ] Ξ → Δ ⊩[ r ] Γ → Δ ⊩[ q ⊔ r ] Ξ ε ◦ ys = ε (xs , x) ◦ ys = (xs ◦ ys) , x [ ys ]
Proposition. The right identity law [ag-000Q]
Proposition. The right identity law [ag-000Q]
{-# OPTIONS --without-K --rewriting #-} module ag-000Q where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N open import ag-000O open import ag-000P
⁺-nat[]v : (i : Γ ⊢[ V ] A) → (xs : Δ ⊩[ q ] Γ) → i [ xs ⁺ B ] = there[ q ] (i [ xs ]) B ⁺-nat[]v here (xs , x) = refl ⁺-nat[]v (there j _) (xs , x) = ⁺-nat[]v j xs [id] : x [ id ] = x [id] {x = here} = refl [id] {x = there i B} = (i [ id ⁺ B ]) =⟨ ⁺-nat[]v {q = V} i id ⟩ there (i [ id ]) B =⟨ ap (λ - → there - B) [id] ⟩ there i B ∎ [id] {x = ` i} = ap `_ [id] [id] {x = t · u} = ((t [ id ]) · (u [ id ])) =⟨ ap (t [ id ] ·_) [id] ⟩ ((t [ id ]) · u) =⟨ ap (_· u) [id] ⟩ (t · u) ∎ [id] {x = ƛ t} = ap ƛ_ [id] ◦id : xs ◦ id = xs ◦id {xs = ε} = refl ◦id {xs = xs , x} = (xs ◦ id) , (x [ id ]) =⟨ ap ((xs ◦ id) ,_) [id] ⟩ (xs ◦ id) , x =⟨ ap (_, x) ◦id ⟩ xs , x ∎
Proposition. Left identity law 與 Associative law [ag-000R]
Proposition. Left identity law 與 Associative law [ag-000R]
{-# OPTIONS --allow-unsolved-metas --without-K --rewriting #-} module ag-000R where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N open import ag-000O open import ag-000P open import ag-000Q
這兩個是 mutual 定義的,而且有一些 goals 我也看不出怎麼解了,暫時就先這樣 xd
tm[] : tm⊑ ⊑t (x [ xs ]) = (tm⊑ ⊑t x) [ xs ] tm[] {x = here} = refl tm[] {x = there x B} = refl tm[] {x = ` x} = tm[] {x = x} tm[] {x = x · x₁} = refl tm[] {x = ƛ x} = refl zero[] : {q : Sort} {r : Sort} {Γ : Con} {Δ : Con} {A : Ty} {xs : Δ ⊩[ r ] Γ} {x : Δ ⊢[ r ] A} → here[ q ] [ xs , x ] = tm⊑ (⊑⊔r {q = q}) x zero[] {q = V} {r = V} = refl zero[] {q = V} {r = T} = refl zero[] {q = T} {r = V} = refl zero[] {q = T} {r = T} = refl tm⊑zero : (q⊑r : q ⊑ r) → here[ r ] = tm⊑ q⊑r here[ q ] tm⊑zero rfl = refl tm⊑zero v⊑t = refl {-# TERMINATING #-} mutual suc[] : (there[ s ] x _) [ ys , y ] = x [ ys ] suc[] {s = V} = refl suc[] {s = T} {x = x} {ys = ys} {y = y} = there[ T ] x _ [ ys , y ] =⟨ refl ⟩ x [ id ⁺ _ ] [ ys , y ] =⟨ [◦] {x = x} ⁻¹ ⟩ x [ (id ⁺ _) ◦ (ys , y) ] =⟨ ap (x [_]) ⁺◦ ⟩ x [ id ◦ ys ] =⟨ ap (x [_]) id◦ ⟩ x [ ys ] ∎ ⁺◦ : xs ⁺ A ◦ (ys , x) = xs ◦ ys ⁺◦ {xs = ε} = refl ⁺◦ {xs = ts , t} {A = A} {ys = ys} {x = x} = ((ts ⁺ A) ◦ (ys , x)) , (there[ _ ] t A [ ys , x ]) =⟨ ap (((ts ⁺ A) ◦ (ys , x)) ,_) (suc[] {x = t}) ⟩ ((ts ⁺ A) ◦ (ys , x)) , (t [ ys ]) =⟨ ap (_, (t [ ys ])) ⁺◦ ⟩ (ts ◦ ys) , (t [ ys ]) ∎ ⁺−nat◦ : {xs : Δ ⊩[ q ] Γ} → {ys : Ξ ⊩[ r ] Δ} → {A : Ty} → xs ◦ (ys ⁺ A) = (xs ◦ ys) ⁺ A ⁺−nat◦ {xs = ε} = refl ⁺−nat◦ {q = q} {r = r} {xs = xs , x} {ys = ys} {A = A} = (xs ◦ (ys ⁺ A)) , (x [ ys ⁺ A ]) =⟨ ap ((xs ◦ (ys ⁺ A)) ,_) (⁺-nat[] {q = q} {B = A} {x = x} {xs = ys}) ⟩ (xs ◦ (ys ⁺ A)) , there[ _ ] (x [ ys ]) A =⟨ ap (_, there[ _ ] (x [ ys ]) A) ⁺−nat◦ ⟩ ((xs ◦ ys) ⁺ A) , there[ _ ] (x [ ys ]) A ∎ ⁺-nat[] : {q r : Sort} → {A B : Ty} → {x : Γ ⊢[ q ] A} → {xs : Δ ⊩[ r ] Γ} → x [ xs ⁺ B ] = there[ q ⊔ r ] (x [ xs ]) B ⁺-nat[] {q = V} {x = i} {xs = xs} = ⁺-nat[]v i xs ⁺-nat[] {q = T} {B = B} {x = x} {xs = xs} = x [ xs ⁺ B ] =⟨ ap (λ - → x [ - ⁺ B ]) (◦id {xs = xs} ⁻¹) ⟩ x [ (xs ◦ id) ⁺ B ] =⟨ ap (x [_]) (⁺−nat◦ ⁻¹) ⟩ x [ xs ◦ (id ⁺ B) ] =⟨ [◦] {x = x} ⟩ x [ xs ] [ id ⁺ B ] =⟨ refl ⟩ there[ T ] (x [ xs ]) B ∎ ↑◦ : {r s : Sort} → {xs : Δ ⊩[ r ] Ξ} → {ys : Γ ⊩[ s ] Δ} → {A : Ty} → (xs ◦ ys) ↑ A = (xs ↑ A) ◦ (ys ↑ A) ↑◦ {r = r} {s = s} {xs = xs} {ys = ys} {A = A} = (xs ◦ ys) ↑ A =⟨ refl ⟩ (xs ◦ ys) ⁺ A , here[ r ⊔ s ] =⟨ ap (λ - → - , here[ _ ]) (⁺−nat◦ ⁻¹) ⟩ xs ◦ (ys ⁺ A) , here[ r ⊔ s ] =⟨ ap (xs ◦ (ys ⁺ A) ,_) (tm⊑zero (⊑⊔r {r = s} {q = r})) ⟩ xs ◦ (ys ⁺ A) , tm⊑ (⊑⊔r {q = r}) here[ s ] =⟨ ap (xs ◦ (ys ⁺ A) ,_) (zero[] {q = r} {r = s} {A = A} {xs = ys ⁺ A} {x = here[ s ]} ⁻¹) ⟩ xs ◦ (ys ⁺ A) , (here[ r ] [ ys ↑ A ]) =⟨ ap (_, (here[ r ] [ ys ↑ A ])) (⁺◦ {xs = xs} {A = A} {ys = ys ⁺ A} {x = here[ s ]} ⁻¹) ⟩ ((xs ⁺ A) ◦ (ys ⁺ A , here[ s ])) , (here[ r ] [ ys ↑ A ]) =⟨ refl ⟩ (xs ↑ A) ◦ (ys ↑ A)∎ [◦] : x [ xs ◦ ys ] = x [ xs ] [ ys ] [◦] {x = here} {xs = xs , x} = refl [◦] {x = there i B} {xs = xs , x} = [◦] {x = i} [◦] {x = ` x} {xs = xs} {ys = ys} = tm⊑ ⊑t (x [ xs ◦ ys ]) =⟨ ap (λ - → tm⊑ ⊑t -) ([◦] {x = x}) ⟩ tm⊑ ⊑t (x [ xs ] [ ys ]) =⟨ tm[] {x = x [ xs ]} ⟩ (tm⊑ ⊑t (x [ xs ]) [ ys ]) ∎ [◦] {x = t · u} {xs = xs} {ys = ys} = (t [ xs ◦ ys ]) · (u [ xs ◦ ys ]) =⟨ ap (_· (u [ xs ◦ ys ])) ([◦] {x = t}) ⟩ (t [ xs ] [ ys ]) · (u [ xs ◦ ys ]) =⟨ ap ((t [ xs ] [ ys ]) ·_) ([◦] {x = u}) ⟩ ((t [ xs ]) [ ys ]) · ((u [ xs ]) [ ys ]) ∎ [◦] {x = ƛ t} {xs = xs} {ys = ys} = ap ƛ_ (t [ (xs ◦ ys) ↑ _ ] =⟨ ap (t [_]) (↑◦ {xs = xs}) ⟩ t [ (xs ↑ _) ◦ (ys ↑ _) ] =⟨ [◦] {x = t} ⟩ (t [ xs ↑ _ ]) [ ys ↑ _ ] ∎) id◦' : Sort → id ◦ xs = xs id◦' {xs = ε} q = refl id◦' {xs = xs , x} q = ap (_, x) (((id ⁺ _) ◦ (xs , x)) =⟨ ⁺◦ ⟩ id ◦ xs =⟨ id◦ ⟩ xs ∎) id◦ : id ◦ xs = xs id◦ = id◦' V {-# INLINE id◦ #-}
到這裡已經證明了 contexts 與 substitutions 真的是一個範疇,而且這個範疇有 terminal object。第五節是把這邊的工作放進去 CwF-simple(constant presheaves 可以讓 CwF 適用於 simply typed calculus)裡,那個我暫時沒什麼興趣。
AI Is Slowly Destroying Your Brain [45VG]
AI Is Slowly Destroying Your Brain [45VG]
新增一些心理學研究結果作為思考 現代 - 商業、科技與政治交織的空間 的案例。
Lie 群的意義 [VQ6V]
Lie 群的意義 [VQ6V]
Lie 群是同時是群跟流形的物件,但這有什麼意義呢?
最簡單的案例是平面旋轉群 ,這是由所有平面上的旋轉組成的群,如果把所有的軌跡都畫到平面上,那這會構成一個 。而我們知道局部的看 可以視為一個直線(切線),這就使得局部的來說,可以用切線近似的討論,這條線被稱為 Lie algebra。

所以我們成功地把曲線問題變成線性問題,更重要的是,這個方法更廣泛來說還是有用,比如很多物理學研究的對稱性可以用某個 Lie 群研究。
另外很有趣的是,Complex number 除了可以用代數的方式定義(see Algebra: Chapter 0, III, Proposition 4.6.):
在 Naive Lie Theory 中提到我們也能用旋轉矩陣來定義。
Lawvere-Tierney topology [math-MRL4]
Lawvere-Tierney topology [math-MRL4]
Let be a topos. A Lawvere-Tierney topology in is a morphism such that the following diagrams are commutative:
A topology in a topos gives rise to a new topos defined over .
Tool. x86-64 Playground [software-9JPJ]
Tool. x86-64 Playground [software-9JPJ]
Definition. Weil algebra [math-T4B2]
Definition. Weil algebra [math-T4B2]
A Weil algebra is an algebra over the rational numbers , equipped with a morphism
such that is a local ring with maximal ideal:
with a nilpotent ideal, and such that is a finite dimensional -vector space.
The notion of Weil algebra makes sense in any topos with a natural numbers object .
Proposition. nilpotent maps form a prime ideal [math-6W2V]
Proposition. nilpotent maps form a prime ideal [math-6W2V]
Definition. Coprimary [local-0]
Definition. Coprimary [local-0]
Let be a Noetherian ring. A nonzero finitely generated -module is coprimary if for all , the multiplication map (reuse element to denote it)
Broken pipe (os error 32)is injective or nilpotent.
If is coprimary, then the set
forms a prime ideal in .
Proof. [local-1]
Proof. [local-1]
To check is a prime ideal, we want to check that if and then .
Because is coprimary, so such are injective, and
the composition of injective maps is injective, hence . □
具體的 Sheaf 以及如何得到 ringed 與 locally ringed space 的定義 [UXEP]
具體的 Sheaf 以及如何得到 ringed 與 locally ringed space 的定義 [UXEP]
Sheaf 的定義是
Definition. Sheaf [math-PPAW]
Definition. Sheaf [math-PPAW]
我們說一個 presheaf 是 sheaf 是指:對所有 open sets in 與所有 的 open covering ,以下兩個條件成立
- Let with for all . Then .
- Given for all such that for all . Then there exists an such that (注意,根據條件一這個 是唯一的)
對我個人比較有意義的案例是
Example. 上的可微分函數 [local-0]
Example. 上的可微分函數 [local-0]
假設 是一個 -manifold(),我們通常用 表示集合
,而 是 的一個開集。這時候 是一個 sheaf of -algebras on
- 這本身也是一個 Ring
- 在這個案例中,stalk 也就變成經典的 function germs(用重合定義的函數局部等價類)。
所以 ringed space 也就定義成了
Definition. Ringed space [math-9M06]
Definition. Ringed space [math-9M06]
Ringed space 是一個 pair
- 一個 topological space
- 一個 sheaf of (commutative) rings
注意到如果 是一個 commutative ring,那 -algebra 也能視為一個 ring (with unit),所以這確實是 manifold 的推廣。
如果進一步要求 的每個 stalk 都是 local ring,那就得到了 locally ringed space:
Definition. Locally Ringed space [math-AYGI]
Definition. Locally Ringed space [math-AYGI]
Locally ringed space 是 ringed space 加上條件:for all
是一個 local ring(i.e. 有 maximal ideal)
語法作為一種檢視方式 [32PV]
語法作為一種檢視方式 [32PV]
正如 Bicameral, Not Homoiconic 一文所述(推薦先看完 Bicameral 再看我這裡寫的東西),真正讓 LISP 脫穎而出的功能,是它 pipeline 特殊的雙層解析器:
- scan 出詞素(token)
- 用 reader 讀出「資料」,通常是一種 form,以 LISP 來說就是 s-expression。而且 reader 會順便讀取 macro 定義跟把 macro 展開
- 最後用 parser 解析成表面語言
根據程式語言的設計會影響實現,有些實現方式會非常多的靜態檢查,以至於在這些實現內部消除了絕大多數的語意錯誤,像是 dependent typed 的語言,這時候我們幾乎可以相信這些編譯器的內部表示跟我們等下提到的客觀語法真的一樣。要注意這並不總是成立,也有很多語意錯誤會被延遲到執行時再處理(如 Python、Racket 的情況),所以在程式語言的實現中,總是假設並依賴一個理想的客觀語法,是由我們規定的語意生成的,我們通常用化簡語意或是指稱語意去研究,而編譯器很大一部分工作就是保證遵循這個語意來實現語言。一套客觀語法可以有很多種檢視方式,比如「指定 a 的新值是整數 1」這個客觀語法可以寫成
- Racket
(set-box! a 1) - C
a = 1; - OCaml
a := 1
更瘋狂一點的話,也不是不能寫成 JSON
{
"assign": {
"variable": "a",
"expression": {
"type": "int",
"val": 1
}
}
}
為什麼表面語法有可能是錯的呢?比如 OCaml 的 parser 不會拒絕 a := 1 的寫法,即使 a 不是 int ref 類型。要到 type checker 的檢查階段,這段程式碼才會因為類型錯誤而被拒絕(這樣就消除了一個語意不正確的表面語句)。
所以一般開發者說的語法,其實可以說是「檢視語法」,當然這並不是說檢視不重要,正如 Concrete syntax matters, actually 說的,好的檢視方式本身就揭示了我們在談論什麼:我當然可以用 * 表示加法、用 + 表示乘法,然後問 3 + 2 * 5 是什麼,但如果有人算錯,我不應該太意外。
所以之所以要視之為檢視,是因為要讓我們可以去想像更好的表示方式,比如
「檢視」暗示了更豐富的運用,像在 proof assistant 的應用中,我們經常想要知道當前 context 可以看到的定義,以及打算證明的目標的類型;在除錯時我們想看到執行期的堆疊等等,都可以考慮為與跟生成客觀語法的語意匹配的檢視方式。
最後,釐清一些常見的誤解
- Bicameral 語法不一定要是 s-expression: Rhombus 使用 Shrubbery Notation
- 不是所有 LISPy 語言都用 list 表示其資料層,Racket 就用了 syntax object 抽象(Bicameral 一文也有說這件事)
MILKY☆SUBWAY [TDJD]
MILKY☆SUBWAY [TDJD]
In Defense of Inefficiency [29QD]
In Defense of Inefficiency [29QD]
Я - extremely composable embeddable programming language [software-000A]
Я - extremely composable embeddable programming language [software-000A]
Extremely composable embeddable programming language
可以先從這些截圖感受一下這什麼程式語言xd



Tool. witr - Why is this running? [software-0009]
Tool. witr - Why is this running? [software-0009]
系統上執行的某個程式或服務 - 無論是 process、service 或綁定到連接埠的程式。都必然有其原因,但這些原因通常間接、不易察覺,或是跨越多個層級,例如監控程式、容器、服務或 shell。而 witr 的用途就是一次展示這些資訊。
Tool. OCaml formatter online configurator [programming-0006]
Tool. OCaml formatter online configurator [programming-0006]
看不懂 OCaml formatter 要怎麼設定?這個專案把排版選項、原始碼跟結果都展示出來,讓人直覺的做出選擇。
Definition. Covering spaces in HoTT [ag-000L]
Definition. Covering spaces in HoTT [ag-000L]
A covering space of a type (space) is a family of sets indexed by .
{-# OPTIONS --safe --without-K #-} module ag-000L where open import MLTT.Spartan hiding (fiber) open import UF.Sets record covering (A : 𝓤 ̇ ) : 𝓤 ⁺ ̇ where constructor cov[_,_] field fiber : A → 𝓤 ̇ fiber-is-set : ∀ (a : A) → is-set (fiber a)
From Zero to QED [lean-0000]
From Zero to QED [lean-0000]
https://sdiehl.github.io/zero-to-qed/01_introduction.html 這個專案教了很多很細節的 tactics,是很好的參考工具。
Eliminator [ag-000K]
Eliminator [ag-000K]
{-# OPTIONS --safe --without-K #-} module ag-000K where open import MLTT.Spartan open import Naturals.Properties
Eliminator of ℕ
ℕ-elim : ∀ (P : ℕ → 𝓤 ̇) → P 0 → (∀ (n : ℕ) → P n → P (succ n)) → (∀ (n : ℕ) → P n) ℕ-elim P P0 Ps zero = P0 ℕ-elim P P0 Ps (succ n) = Ps n (ℕ-elim P P0 Ps n)
Define with pattern matching
plus : ℕ → ℕ → ℕ plus zero b = b plus (succ a) b = succ (plus a b) mul : ℕ → ℕ → ℕ mul zero c = zero mul (succ a) b = plus b (mul a b) exp : ℕ → ℕ → ℕ exp x zero = 1 exp x (succ k) = mul x (exp x k)
Now use the eliminator to define them
plus' : ℕ → ℕ → ℕ plus' x = ℕ-elim (λ _ → ℕ → ℕ) (λ z → z) (λ x' plus-x' → λ y → succ (plus-x' y)) x t5 : plus' 1 1 = 2 t5 = refl p1 : (a b : ℕ) → plus a b = plus' a b p1 zero b = refl p1 (succ a) b = succ (plus a b) =⟨ ap succ (p1 a b) ⟩ succ (plus' a b) =⟨by-definition⟩ succ (ℕ-elim (λ _ → ℕ → ℕ) (λ z → z) (λ x' plus-x' → λ y → succ (plus-x' y)) a b) =⟨by-definition⟩ plus' (succ a) b ∎ mul' : ℕ → ℕ → ℕ mul' x = ℕ-elim (λ _ → ℕ → ℕ) (λ z → zero) (λ x' mul-x' → λ y → plus' y (mul-x' y)) x t7 : mul' 0 1 = 0 t7 = refl t8 : mul' 1 1 = 1 t8 = refl t9 : mul' 2 2 = 4 t9 = refl p2 : (a b : ℕ) → mul a b = mul' a b p2 zero b = refl p2 (succ a) zero = p2 a 0 p2 (succ a) (succ b) = plus (succ b) (mul a (succ b)) =⟨ p1 (succ b) (mul a (succ b)) ⟩ plus' (succ b) (mul a (succ b)) =⟨ ap (plus' (succ b)) (p2 a (succ b)) ⟩ plus' (succ b) (mul' a (succ b)) =⟨by-definition⟩ mul' (succ a) (succ b) ∎ exp' : ℕ → ℕ → ℕ exp' x y = ℕ-elim (λ _ → ℕ → ℕ) (λ x → 1) (λ y' exp-y' → λ x → mul' x (exp-y' x)) y x t10 : exp' 2 0 = 1 t10 = refl t11 : exp' 2 10 = 1024 t11 = refl p3 : (a b : ℕ) → exp a b = exp' a b p3 a zero = refl p3 zero (succ b) = refl p3 (succ a) (succ b) = exp (succ a) (succ b) =⟨by-definition⟩ mul (succ a) (exp (succ a) b) =⟨ p2 (succ a) (exp (succ a) b) ⟩ mul' (succ a) (exp (succ a) b) =⟨ ap (mul' (succ a)) (p3 (succ a) b) ⟩ mul' (succ a) (exp' (succ a) b) =⟨by-definition⟩ exp' (succ a) (succ b) ∎
Plus commutative yoga
C : commutative plus C zero zero = refl C zero (succ b) = succ b =⟨ ap succ (C 0 b) ⟩ succ (plus b zero) ∎ C (succ a) zero = succ (plus a 0) =⟨ ap succ (C a 0) ⟩ succ (plus 0 a) =⟨ refl ⟩ plus 0 (succ a) ∎ C (succ a) (succ b) = succ (plus a (succ b)) =⟨ ap succ (C a (succ b)) ⟩ succ (plus (succ b) a) =⟨ ap succ refl ⟩ succ (succ (plus b a)) =⟨ ap (λ x → succ (succ x)) (C b a) ⟩ succ (succ (plus a b)) =⟨ ap succ refl ⟩ succ (plus (succ a) b) =⟨ ap succ (C (succ a) b) ⟩ succ (plus b (succ a)) ∎
Remind
add1 : ℕ → ℕ add1 = ℕ-elim (λ _ → ℕ) (succ zero) λ _ n → succ n t1 : add1 0 = 1 t1 = refl double' : ℕ → ℕ double' = ℕ-elim (λ _ → ℕ) zero λ _ mn → succ (succ mn) t2 : double' 0 = 0 t2 = refl t3 : double' 1 = 2 t3 = refl t4 : double' 2 = 4 t4 = refl
M-type (the type of non-well-founded, labelled trees) [ag-000J]
M-type (the type of non-well-founded, labelled trees) [ag-000J]
{-# OPTIONS --cubical --guardedness --two-level --no-level-universe #-} module ag-000J where open import Cubical.Foundations.Prelude open import Cubical.Data.Sum open import Cubical.Data.Nat data 𝟘 : Type where data 𝟙 : Type where ⋆ : 𝟙 data Maybe (X : Type) : Type where none : Maybe X some : X → Maybe X record ℕ∞ : Type where coinductive field pred∞ : Maybe ℕ∞
M-type 是 non-well-formed, labelled trees
的型別,有可能有有限也可能有無限長的 path。 M 是 strictly
positive coinductive types 的 universal type。
record M (S : Type) (P : S → Type) : Type where coinductive field shape : S pos : P shape → M S P
M S P 代表了 conatural number
module conatural-number where open ℕ∞ open M S = 𝟙 ⊎ 𝟙 P : S → Type P (inl _) = 𝟘 P (inr _) = 𝟙 N∞ = M S P inf : ℕ∞ pred∞ inf = none inf' : ℕ∞ pred∞ inf' = some inf i : N∞ shape i = inl ⋆ pos i = λ () i' : N∞ shape i' = inr ⋆ pos i' = λ x → i
W-type (the type of well-founded, labelled trees) [ag-000I]
W-type (the type of well-founded, labelled trees) [ag-000I]
{-# OPTIONS --cubical --guardedness --two-level --no-level-universe #-} module ag-000I where open import Cubical.Foundations.Prelude open import Cubical.Data.Sum open import Cubical.Data.Nat data 𝟘 : Type where data 𝟙 : Type where ⋆ : 𝟙
W-type (due to Martin-Löf) 是 well-founded, labelled
trees 的型別。每棵 W-type 的樹都可以有無限多分支,但 path
都是有限長。W 有兩個參數
S : Type表示 shapeP : S → Type表示有(P s)-many positions
W 是 strictly positive inductive types 的 universal
type。
data W (S : Type) (P : S → Type) : Type where sup-W : (s : S) → (P s → W S P) → W S P
Example: 自然數
module natural-number where S = 𝟙 ⊎ 𝟙 P : S → Type P (inl _) = 𝟘 -- therefore, in this direction cannot go further P (inr _) = 𝟙 -- this direction has one continuation N = W S P z : N z = sup-W (inl ⋆) λ () s : N → N s n = sup-W (inr ⋆) λ ⋆ → n α : ℕ → N α zero = z α (suc n) = s (α n) β : N → ℕ β (sup-W (inl ⋆) x) = zero β (sup-W (inr ⋆) f) = suc (β (f ⋆)) main : (n : ℕ) → β (α n) ≡ n main zero = β (α zero) ≡⟨ refl ⟩ β z ≡⟨ refl ⟩ zero ∎ main (suc n) = cong suc (main n) main⁻¹ : (n : N) → α (β n) ≡ n main⁻¹ (sup-W (inl ⋆) f) = α (β (sup-W (inl ⋆) f)) ≡⟨ refl ⟩ z ≡⟨ refl ⟩ sup-W (inl ⋆) (λ ()) ≡⟨ cong (sup-W (inl ⋆)) (sym (funExt λ ())) ⟩ sup-W (inl ⋆) f ∎ main⁻¹ (sup-W (inr ⋆) f) = α (β (sup-W (inr ⋆) f)) ≡⟨ refl ⟩ α (suc (β (f ⋆))) ≡⟨ refl ⟩ s (α (β (f ⋆))) ≡⟨ refl ⟩ sup-W (inr ⋆) (λ _ → α (β (f ⋆))) ≡⟨ cong (sup-W (inr ⋆)) (funExt t) ⟩ sup-W (inr ⋆) f ∎ where t : (x : 𝟙) → α (β (f ⋆)) ≡ f x t ⋆ = main⁻¹ (f ⋆)
Simplex category 與 face maps [math-001I]
Simplex category 與 face maps [math-001I]
根據定義,每個 simplicial set 都是 simplex category 的一個 presheaf
Definition. Simplex Category [local-0]
Definition. Simplex Category [local-0]
- Ob: 每個 object 都是 並帶有整數的 order 結構(其中 是非負整數)
- Hom: 每個 morphism 都是嚴格遞增函數
這些 morphism 可以用一類特殊的 maps 組出來,叫做 face maps,舉例來說
Broken pipe (os error 32)這個定義乍一看實在沒辦法理解這在定義什麼,所以要實際看看幾個案例:從 到 可以畫成
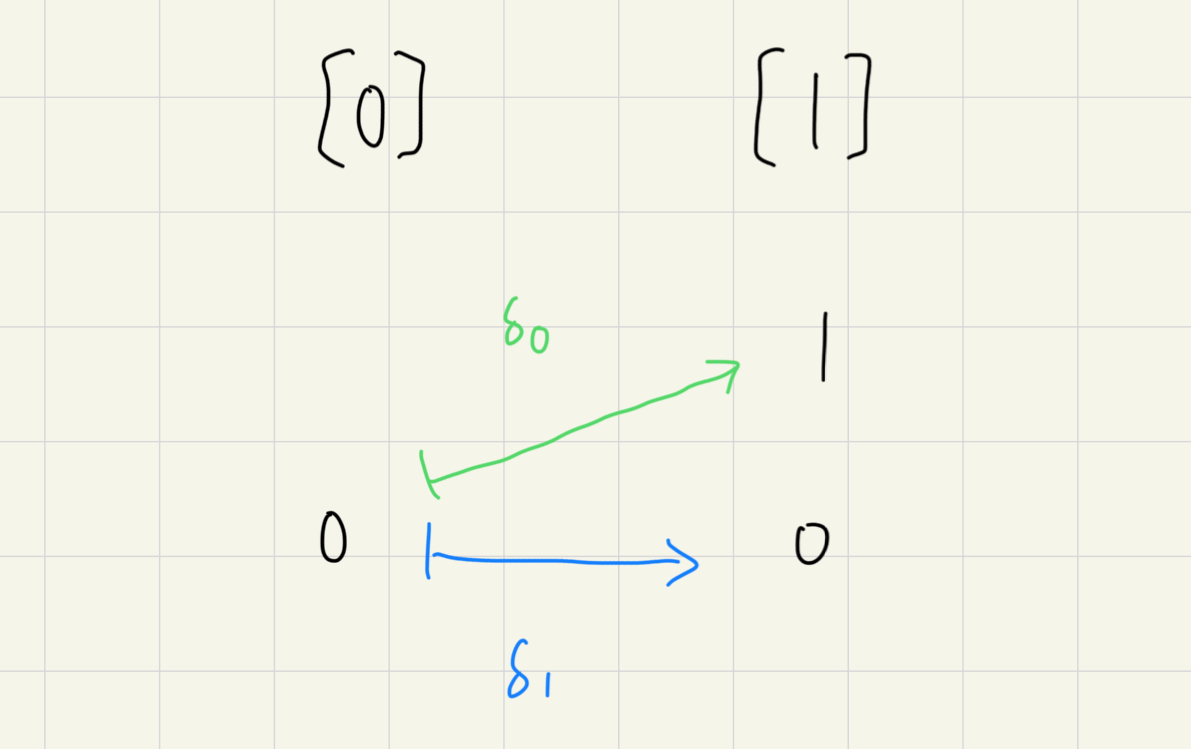
從 到 可以畫成
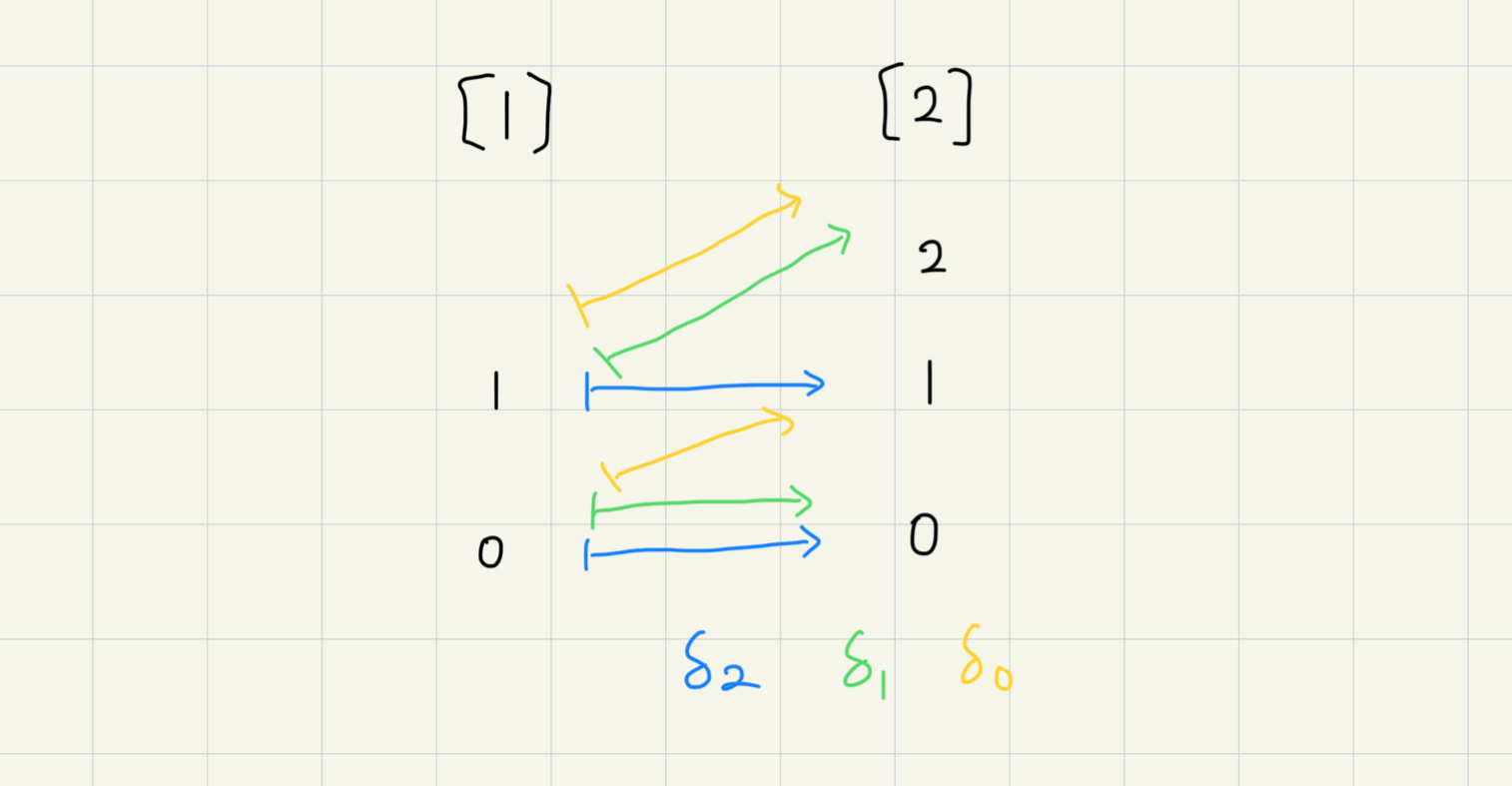
事實上,如果畫成 simplex 的幾何表示 就更明顯了:
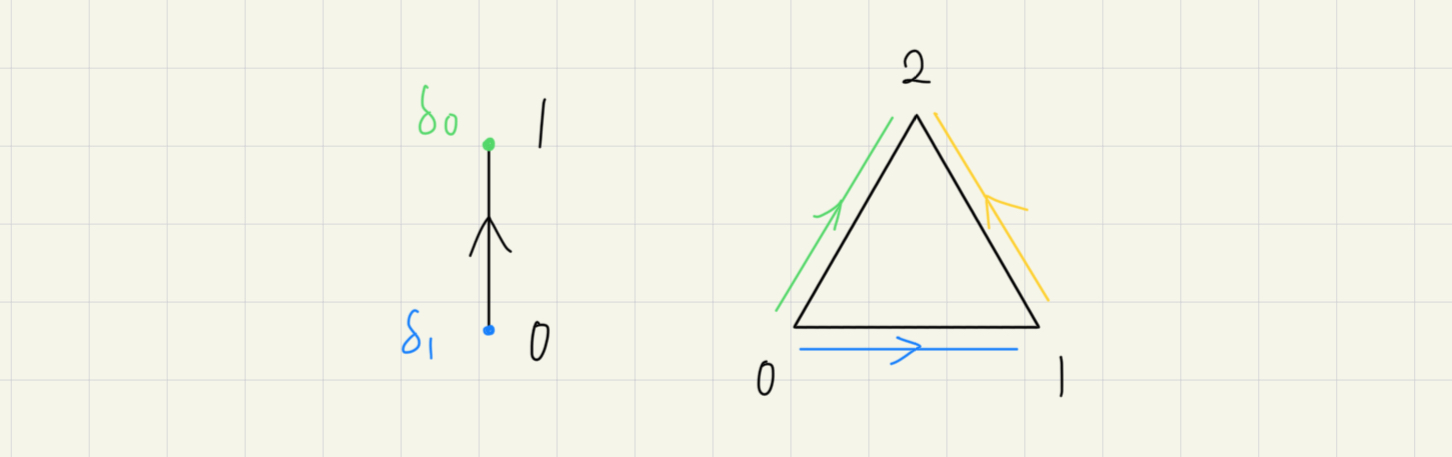
標準 -simplex 可以定義成:
所以 face maps 就是在表示 表示 的哪一個邊界,線的邊界是兩個點,面的邊界是三條線。
沒有內接矩形的平面曲線 [math-001H]
沒有內接矩形的平面曲線 [math-001H]
在看過
之後的一點嘗試。
就我的認知,有限多的 singular points 無法破壞這裡的拓墣特性,所以討論非碎形曲線的時候,頂多討論能夠減少內接矩形到什麼程度。所以我真正有興趣的是局部構成沒有內接矩形時,如何重複這個構成還是保持特性。
然而一次跨出這步太超出我目前所知了,所以只能先考慮相關的變形問題:首先,開放的曲線可能沒有內接矩形,比如下圖由兩個有界直線構成(箭頭表示無限延伸方向)
- 如果選擇了頂點與其中一邊的點,那麼法向只能再跟此圖交於一點,無法構成矩形。另一邊因為對稱性所以一樣。
- 如果選擇一邊的兩點,那法向接觸到另一邊的長度不同,自然也不是矩形。
- 如果一邊各自選一點,因為這條邊往任意一邊移動都會改變長度,也沒辦法構成矩形。
但這張圖如果稍作修改,比如加一個直線拉回來變成三角形,就會再次有內接矩形。
另一種值得考慮的基本構造是圓,因為可以說圓的內接矩形有無限多個,但也可以說某種程度上只有一個內接矩形。所以如果考慮取半圓形,另一半則是想辦法破壞對稱性,比如我考慮過的其中一種形狀是

想法就是一直取一半直徑的半圓去填右半部。這個旋轉一下就可以弄成方程組,所以要驗證這個圖形可以嘗試看看方程組中出現矩形要怎麼驗證。
Formal Topology in UF [math-001G]
Formal Topology in UF [math-001G]
Reading https://github.com/ayberkt/formal-topology-in-UF and use TypeTopology to understand
Definition. Poset [ag-000F]
Definition. Poset [ag-000F]
{-# OPTIONS --safe --without-K #-} module ag-000F where open import MLTT.Spartan open import UF.Sets open import UF.SubtypeClassifier
Order is a binary relation ≤.
order-structure : 𝓤 ̇ → 𝓤 ⁺ ̇ order-structure {𝓤} A = A → A → Ω 𝓤
A poset A is a pair (A, ≤ )
- x ≤ x for all x ∈ A
- x ≤ y and y ≤ z implies x ≤ z for all x, y, z ∈ A
- x ≤ y and y ≤ x implies x = y for all x, y ∈ A
poset-axioms : (A : 𝓤 ̇ ) → order-structure A → 𝓤 ̇ poset-axioms A _≤_ = is-set A × ((x : A) → (x ≤ x) holds) × ((x y z : A) → (x ≤ y) holds → (y ≤ z) holds → (x ≤ z) holds) × ((x y : A) → (x ≤ y) holds → (y ≤ x) holds → x = y) Poset-structure : 𝓤 ̇ → 𝓤 ⁺ ̇ Poset-structure A = Σ _≤_ ꞉ order-structure A , (poset-axioms A _≤_) Poset : (𝓤 : Universe) → 𝓤 ⁺ ̇ Poset 𝓤 = Σ A ꞉ 𝓤 ̇ , Poset-structure A
We can add a helper to extract underlying set
⟨_⟩ : {S : 𝓤 ̇ → 𝓥 ̇ } → Σ S → 𝓤 ̇ ⟨ X , s ⟩ = X order-of : (P : Poset 𝓤) → ⟨ P ⟩ → ⟨ P ⟩ → Ω 𝓤 order-of (X , _≤_ , _) x y = x ≤ y syntax order-of P x y = x ≤⟨ P ⟩ y posets-are-sets : (P : Poset 𝓤) → is-set ⟨ P ⟩ posets-are-sets (X , _≤_ , i , rfl , trans , ir) = i
A hom from a poset to another, is a map that preserves the order
is-hom : (P : Poset 𝓤) (Q : Poset 𝓥) → (⟨ P ⟩ → ⟨ Q ⟩) → 𝓤 ⊔ 𝓥 ̇ is-hom P Q f = ∀ {x y} → (x ≤⟨ P ⟩ y) holds → (f x ≤⟨ Q ⟩ f y) holds
Identity map is a hom
id-is-hom : (P : Poset 𝓤) → is-hom P P id id-is-hom P x≤y = x≤y
The composition of homs is a hom
∘-is-hom : (P : Poset 𝓤) (Q : Poset 𝓥) (R : Poset 𝓦) (f : ⟨ P ⟩ → ⟨ Q ⟩) (g : ⟨ Q ⟩ → ⟨ R ⟩) → is-hom P Q f → is-hom Q R g → is-hom P R (g ∘ f) ∘-is-hom P Q R f g f-is-hom g-is-hom x≤y = g-is-hom (f-is-hom x≤y)
Definition. Frame [ag-000G]
Definition. Frame [ag-000G]
{-# OPTIONS --safe --without-K #-} module ag-000G where open import MLTT.Spartan open import UF.SubtypeClassifier open import ag-000F
To build frame, we must be able to talk about arbitrary subsets of underlying set X
Fam : 𝓤 ̇ → 𝓤 ⁺ ̇ Fam {𝓤} A = Σ I ꞉ 𝓤 ̇ , (I → A) module JoinStntax {A : 𝓤 ̇ } (join : Fam A → A) where join-of : {I : 𝓤 ̇ } → (I → A) → A join-of {I} f = join (I , f) syntax join-of (λ i → e) = ∨⟨ i ⟩ e index : {X : 𝓤 ̇ } → Fam X → 𝓤 ̇ index (I , _) = I _$_ : {X : 𝓤 ̇ } → (F : Fam X) → index F → X _$_ (_ , f) = f infixl 40 _$_ _∈_ : {X : 𝓤 ̇ } → X → Fam X → 𝓤 ̇ x ∈ (_ , f) = fiber f x
Beside poset axioms, frame axioms are
- There is a top element ⊤, every element x ≤ ⊤
- Binary meet x ∧ y is smaller than x and y, and it is a limit
- Each arbitrary subset U has a join ∨U, such that each element of it smaller than the join
- Binary meets must distribute over arbitrary joins
frame-axioms : (X : 𝓤 ̇ ) → order-structure X → X → (X → X → X) → (Fam X → X) → 𝓤 ⁺ ̇ frame-axioms X _≤_ ⊤ _∧_ ∨ = ((x : X) → (x ≤ ⊤) holds) × ((x y : X) → ((x ∧ y) ≤ x) holds × ((x ∧ y) ≤ y) holds) × ((x y z : X) → (z ≤ x) holds → (z ≤ y) holds → (z ≤ (x ∧ y)) holds) × ((U : Fam X) → (x : X) → x ∈ U → (x ≤ ∨ U) holds) × ((U : Fam X) → (x : X) → ((y : X) → y ∈ U → (y ≤ x) holds) → (∨ U ≤ x) holds) × distrib where open JoinStntax ∨ distrib = ((U : Fam X) → (x : X) → x ∧ (∨ U) = ∨⟨ i ⟩ (x ∧ U $ i)) Frame-structure : 𝓤 ̇ → 𝓤 ⁺ ̇ Frame-structure X = Σ _≤_ ꞉ order-structure X , Σ ⊤ ꞉ X , Σ _∧_ ꞉ (X → X → X) , Σ ∨ ꞉ (Fam X → X) , (poset-axioms X _≤_) × (frame-axioms X _≤_ ⊤ _∧_ ∨) Frame : (𝓤 : Universe) → 𝓤 ⁺ ̇ Frame 𝓤 = Σ X ꞉ 𝓤 ̇ , Frame-structure X
Properties of frames [ag-000H]
Properties of frames [ag-000H]
{-# OPTIONS --safe --without-K #-} module ag-000H where open import MLTT.Spartan open import UF.SubtypeClassifier open import ag-000F open import ag-000G
In frames, meet is commutative, hence no difference between x ∧ y and y ∧ x
meet-is-comm : (F : Frame 𝓤) → (x y : ⟨ F ⟩) → 𝓤 ̇ meet-is-comm (X , _≤_ , ⊤ , _∧_ , _ ) x y = x ∧ y = y ∧ x prove-meet-is-comm : (F : Frame 𝓤) → (x y : ⟨ F ⟩) → meet-is-comm F x y prove-meet-is-comm (X , _≤_ , ⊤ , _∧_ , ∨ , (_ , _ , _ , split) , (_ , meet , lim , _ , _) ) x y = split (x ∧ y) (y ∧ x) I II where I : ((x ∧ y) ≤ (y ∧ x)) holds I = lim y x (x ∧ y) (meet x y .pr₂) (meet x y .pr₁) II : ((y ∧ x) ≤ (x ∧ y)) holds II = lim x y (y ∧ x) (meet y x .pr₂) (meet y x .pr₁)
Matrix representation of complex numbers [math-001F]
Matrix representation of complex numbers [math-001F]
To see why
behave same as the complex numbers is to write as a linear combination:
and hence we are wondering, what if we define
and multiplication as matrix multiplication, addition as matrix addition? Are these behave same as complex numbers? Since is the identity matrix, we simply get followings
we would like to know if :
as desired. Then we also know linear combinations based on and maps to complex numbers bijectively:
so now we can see this indeed is a representation of complex numbers.
旋轉矩陣的 product 是給定角度的相加 [ag-000E]
旋轉矩陣的 product 是給定角度的相加 [ag-000E]
{-# OPTIONS --without-K #-} module ag-000E where open import MLTT.Spartan hiding (_+_; _×_) open import MLTT.Fin
因為不想引入太多其餘結構,把實數跟三角函數的一些性質直接公理化來用
module _ (ℝ : 𝓤₀ ̇) where variable a b : ℝ postulate cos : ℝ → ℝ sin : ℝ → ℝ -_ : ℝ → ℝ _+_ : ℝ → ℝ → ℝ _×_ : ℝ → ℝ → ℝ tri1 : cos (a + b) = cos a × cos b + - (sin a × sin b) tri2 : sin (a + b) = sin a × cos b + sin b × cos a ℝ-neg-1 : a × - b = - (a × b) ℝ-neg-add : - a + - b = - (a + b) ℝ-+-comm : a + b = b + a ℝ-×-comm : a × b = b × a infixl 60 -_ infixl 40 _+_ infixl 50 _×_ ℝ-neg-2 : - a × b = - (a × b) ℝ-neg-2 {a}{b} = - a × b =⟨ ℝ-×-comm ⟩ b × - a =⟨ ℝ-neg-1 ⟩ - (b × a) =⟨ ap -_ ℝ-×-comm ⟩ - (a × b) ∎
矩陣可以看成由兩個索引指向某其 Field K 的元素的型別
Matrix : (m n : ℕ) → (K : 𝓤 ̇) → 𝓤 ̇ Matrix m n K = Fin m → Fin n → K
只定義 2 × 2 的矩陣乘法
_⊗_ : Matrix 2 2 ℝ → Matrix 2 2 ℝ → Matrix 2 2 ℝ _⊗_ m n 𝟎 𝟎 = m 𝟎 𝟎 × n 𝟎 𝟎 + m 𝟎 𝟏 × n 𝟏 𝟎 _⊗_ m n 𝟎 𝟏 = m 𝟎 𝟎 × n 𝟎 𝟏 + m 𝟎 𝟏 × n 𝟏 𝟏 _⊗_ m n 𝟏 𝟎 = m 𝟏 𝟎 × n 𝟎 𝟎 + m 𝟏 𝟏 × n 𝟏 𝟎 _⊗_ m n 𝟏 𝟏 = m 𝟏 𝟎 × n 𝟎 𝟏 + m 𝟏 𝟏 × n 𝟏 𝟏 infixl 30 _⊗_
旋轉矩陣它本人,這個用來表示 Rθ,其中 θ ∈ ℝ 是角度的值
R : ℝ → Matrix 2 2 ℝ R θ 𝟎 𝟎 = cos θ R θ 𝟎 𝟏 = sin θ R θ 𝟏 𝟎 = - sin θ R θ 𝟏 𝟏 = cos θ
證明目標:RθRφ = Rθ + φ
證明方式就是按 component 去證明等式成立。
thm : {θ φ : ℝ} (i j : Fin 2) → (R θ ⊗ R φ) i j = R (θ + φ) i j thm {θ}{φ} 𝟎 𝟎 = (R θ ⊗ R φ) 𝟎 𝟎 =⟨by-definition⟩ cos θ × cos φ + sin θ × (- sin φ) =⟨ ap (cos θ × cos φ +_) ℝ-neg-1 ⟩ cos θ × cos φ + - (sin θ × sin φ) =⟨ tri1 ⁻¹ ⟩ cos (θ + φ) =⟨by-definition⟩ R (θ + φ) 𝟎 𝟎 ∎ thm {θ}{φ} 𝟎 𝟏 = (R θ ⊗ R φ) 𝟎 𝟏 =⟨by-definition⟩ cos θ × sin φ + sin θ × cos φ =⟨ ℝ-+-comm ⟩ sin θ × cos φ + cos θ × sin φ =⟨ ap (sin θ × cos φ +_) ℝ-×-comm ⟩ sin θ × cos φ + sin φ × cos θ =⟨ tri2 ⁻¹ ⟩ sin (θ + φ) =⟨by-definition⟩ R (θ + φ) 𝟎 𝟏 ∎ thm {θ}{φ} 𝟏 𝟎 = (R θ ⊗ R φ) 𝟏 𝟎 =⟨by-definition⟩ (- sin θ) × cos φ + cos θ × (- sin φ) =⟨ ap (_+ cos θ × - sin φ) ℝ-neg-2 ⟩ - (sin θ × cos φ) + cos θ × (- sin φ) =⟨ ap (- (sin θ × cos φ) +_) ℝ-neg-1 ⟩ - (sin θ × cos φ) + - (cos θ × sin φ) =⟨ ℝ-neg-add ⟩ - (sin θ × cos φ + cos θ × sin φ) =⟨ ap -_ (ap (sin θ × cos φ +_) ℝ-×-comm) ⟩ - (sin θ × cos φ + sin φ × cos θ) =⟨ ap -_ (tri2 ⁻¹) ⟩ - sin (θ + φ) =⟨by-definition⟩ R (θ + φ) 𝟏 𝟎 ∎ thm {θ}{φ} 𝟏 𝟏 = (R θ ⊗ R φ) 𝟏 𝟏 =⟨by-definition⟩ - sin θ × sin φ + cos θ × cos φ =⟨ ℝ-+-comm ⟩ cos θ × cos φ + - sin θ × sin φ =⟨ ap (cos θ × cos φ +_) ℝ-neg-2 ⟩ cos θ × cos φ + - (sin θ × sin φ) =⟨ tri1 ⁻¹ ⟩ R (θ + φ) 𝟏 𝟏 ∎ addition : {θ φ : ℝ} (i j : Fin 2) → (R θ ⊗ R φ) i j = (R φ ⊗ R θ) i j addition {θ} {φ} i j = (R θ ⊗ R φ) i j =⟨ thm i j ⟩ R (θ + φ) i j =⟨ ap (λ x → R x i j) ℝ-+-comm ⟩ R (φ + θ) i j =⟨ thm i j ⁻¹ ⟩ (R φ ⊗ R θ) i j ∎
Streams and finite observations [ag-000D]
Streams and finite observations [ag-000D]
From Topology via logic
{-# OPTIONS --safe --without-K --guardedness --no-exact-split #-} module ag-000D where open import MLTT.Spartan open import MLTT.List
Stream can be defined as a coinductive record.
record Stream (A : 𝓤 ̇ ) : 𝓤 ̇ where coinductive constructor _∷_ field head : A tail : Stream A open Stream
For example a stream of all zero.
zeros : Stream 𝟚 head zeros = ₀ tail zeros = zeros
s ⊨starts o defines a relation that a stream can be
realized by a finite observation.
_⊨starts_ : Stream 𝟚 → List 𝟚 → 𝓤₀ ̇ s ⊨starts [] = ₀ = ₀ s ⊨starts (x ∷ xs) = (x = head s) × (tail s ⊨starts xs)
For example, the first bit zeros produces is
₀.
first-bit : zeros ⊨starts [ ₀ ] first-bit = refl , refl
Every stream can be realized by “no” observation.
realize-by-no-observation : (s : Stream 𝟚) → s ⊨starts [] realize-by-no-observation s = refl
We can define order relation for these finite observations.
_⊇_ : List 𝟚 → List 𝟚 → 𝓤₀ ̇ _ ⊇ [] = ₀ = ₀ [] ⊇ _ = 𝟘 (x ∷ l) ⊇ (x₁ ∷ l2) = (x = x₁) × (l ⊇ l2)
This order has antisymmetric
eq-condition : (l1 l2 : List 𝟚) → l1 ⊇ l2 → l2 ⊇ l1 → l1 = l2 eq-condition [] [] p q = refl eq-condition (x ∷ l1) (y ∷ l2) (ph , pt) (qh , qt) = x ∷ l1 =⟨ ap (_∷ l1) ph ⟩ y ∷ l1 =⟨ ap (y ∷_) (eq-condition l1 l2 pt qt) ⟩ y ∷ l2 ∎
, in fact total, which means a boring order. The order induces refinement of observations: if a observation is subsequence of another observation that realise the stream, then the stream also be realized by this subsequence.
refine-observation : {s : Stream 𝟚} → (l l2 : List 𝟚) → s ⊨starts l → l ⊇ l2 → s ⊨starts l2 refine-observation l2 [] _ _ = refl refine-observation (x ∷ l) (y ∷ l2) (x=head , tail) (x=y , rest) = (x=y ⁻¹ ∙ x=head) , refine-observation l l2 tail rest
Dependent equality in dependent type theory [ag-000C]
Dependent equality in dependent type theory [ag-000C]
這是從 https://mathstodon.xyz/@MartinEscardo/114751426538568913 學到的技巧。
{-# OPTIONS --safe --without-K #-} module ag-000C where open import Agda.Primitive renaming (Set to Type; Setω to Typeω) open import Agda.Builtin.Equality open import Agda.Builtin.Nat
假設我們有
- a type
X : Type - a family of types
A : X → Typeindexed byX
那我們常常會遇到有
x y : Xa : A xb : A yp : x = y
= 是 MLTT 的 identity type,p 是一個
x = y 的證明,這時候如果我們問 a = b
是沒有答案的,因為根據 MLTT,a 跟 b
的類型壓根兒就不一樣,這導致問題連寫都寫不下來,那怎麼辦?
方法是定義高階等式(又稱為 dependent equality 或是 PathOver 或是 path transport),在該依賴項等價的情況下把問題變成新的等式來讓 dependent type 語言表達等式
用案例來說就是如果有個 equality 是「類型不同」的(出於依賴項的不透明性,比如這裡 vector length 輸入的 associative 不同)
先定義一些下面案例會用到的輔助程式:
cong : {X Y : Type} (f : X → Y) {x₀ x₁ : X} → x₀ ≡ x₁ → f x₀ ≡ f x₁ cong {X} {Y} f refl = refl +-assoc : ∀ l m n → (l + m) + n ≡ l + (m + n) +-assoc zero m n = refl +-assoc (suc l) m n = cong suc (+-assoc l m n)
具體案例 vector ++ 的 associativity
data Vec (A : Type) : Nat → Type where [] : Vec A 0 _::_ : ∀{n} → A → Vec A n → Vec A (suc n) infixl 40 _::_ _++_ : {Y : Type} {l m : Nat} → (xs : Vec Y l) → (ys : Vec Y m) → Vec Y (l + m) [] ++ ys = ys (x :: xs) ++ ys = x :: (xs ++ ys) infixl 30 _++_
基於 x₀ ≡ x₁ 定義一個更高階的 equality
higher-equality : {X : Type} (A : X → Type) {x₀ x₁ : X} → A x₀ → x₀ ≡ x₁ → A x₁ → Type higher-equality A a₀ refl a₁ = a₀ ≡ a₁
但可以根據案例定義比較簡單的版本
_≡[_]_ : {X : Type} {x₀ x₁ : Nat} → Vec X x₀ → x₀ ≡ x₁ → Vec X x₁ → Type a₀ ≡[ refl ] a₁ = a₀ ≡ a₁
命題 (xs ++ ys) ++ zs ≡ xs ++ (ys ++ zs)
無法寫下,因為(meta-level 的)型別不同。 所以需要用高階等式描述
cong-cons : {X : Type} {m n : Nat} {xs : Vec X m} {ys : Vec X n} (x : X) (p : m ≡ n) → xs ≡[ p ] ys → x :: xs ≡[ cong suc p ] x :: ys cong-cons {X}{A} x refl refl = refl ++-assoc : {X : Type} (l m n : Nat) (xs : Vec X l) (ys : Vec X m) (zs : Vec X n) → (xs ++ ys) ++ zs ≡[ +-assoc l m n ] xs ++ (ys ++ zs) ++-assoc {X} zero m n [] ys zs = refl ++-assoc {X} (suc l) m n (x :: xs) ys zs = I where I : x :: (xs ++ ys) ++ zs ≡[ cong suc (+-assoc l m n) ] x :: (xs ++ (ys ++ zs)) I = cong-cons x (+-assoc l m n) (++-assoc l m n xs ys zs)
Second-Order Generalised Algebraic Theories: Signatures and First-Order Semantics [tt-000U]
Second-Order Generalised Algebraic Theories: Signatures and First-Order Semantics [tt-000U]
NOTE about Second-Order Generalised Algebraic Theories: Signatures and First-Order Semantics
這篇文章主要在探討程式語法的表示方式,並展示如何結合代數方法跟 HOAS。作者說他們跟隨 Uemura 把語言定義成 second-order generalised algebraic theories (SOGATs),通過一系列案例揭示 non-substructural languages 可以自然的定義成 SOGATs
- SOGAT 的形式定義 (using the syntax of a particular SOGAT)
- 定義兩種 SOGAT signatures 到 GAT signatures (signatures for quotient inductive-inductive types) 的轉換,分別基於同時替換(parallel substitution)與單一替換(single substitution)
按代數抽象程度區分 [local-0]
按代數抽象程度區分 [local-0]
從具體到抽象可以把語法表示看成
| 語法表示 | 能力 |
| abstract syntax trees (AST) | 把程式原文 parse 後直接儲存用的一系列資料結構 |
| well-scoped syntax tree | λx.x 跟 λy.y 在這類表示法裡面無法區分,也就是說綁定使用的具體名稱不再重要 |
| intrinsic well-typed terms | 這種表示把語法跟 typing relation 整合,所以 non well-typed 的程式甚至無法表達 |
| well-typed, quotiented by the conversion relation (GAT) | 加上更多 well-formness relation 的推廣代數理論,下面介紹 |
| SOGAT | GAT 推到 second-order,下面介紹 |
在 well-typed terms 上再加上 conversion relation 就變成廣義代數理論(generalised algebraic theory,簡稱 GAT),GAT 用來處理 dependently typed languages 時特別方便,因為 typing 依賴了 conversion relation。在 GAT 上只能定義保留了 conversion relation 的函數,因此連印出函數都無法定義,但 normalisation(正規化)、typechecking(型別檢查)跟 parametricity 這些函數保留 conversion 因此可定義。
對任何 GAT 來說,syntax 可以定義成 initial model,因此沒有區分語法跟語意的必要,某種意義上來說,一個程式語言就是一個 GAT。
HOAS 方法:按對 bindings/variables 的處理方式區分 [local-1]
HOAS 方法:按對 bindings/variables 的處理方式區分 [local-1]
HOAS 觀點關心 bindings 跟 variables 的處理方式,比如 De Bruijn indices 使名稱選擇與語意無關,但這也表示替換必須是語法的一部分,舉例來說 form of a category with families。
Logical frameworks 跟 higher-order abstract syntax (HOAS) 提供了另一種實現 bindings 跟 variables 的方式:使用 metatheory 的函數空間。
舉例來說,pure lambda calculus 的 lambda operation 的 type 是二階函數空間 (Tm → Tm) → Tm。這在理論上的解釋是 type-theoretic internal language of presheaves over the category of contexts and syntactic substitutions,在這個 topos 的 internal language 裡,lambda 的類型就長那樣。
Internal language 的觀點可以用來定義程式語言是什麼:有綁定的語言不是一個 GAT,而是一個二階的廣義代數理論(second-order generalised algebraic theory,簡稱 SOGAT),這種理論可以有二階操作(但不是任意高階)。
Untyped 或是 Simply typed 都有被定義成二階理論過,但 Uemura 是第一個用 SOGATs 定義有綁定的語言的人。這個理論真的很厲害,一個語言的 SOGAT 定義比 well-typed quotiented 定義還要抽象:SOGAT 連 contexts 跟 substitutions 都不用提到,這些會自動生成。但這不是一個 well-behaved 的代數理論,比如 second-order models 之間沒有有意義的 homomorphism。
為了描述 SOGAT 的一階模型、homomorphisms 或是 syntax 的 notion,作者把它轉成一個 GAT。這個過程中引入新的 sorts 給 contexts 跟 substitutions,然後把每個操作都用其 context index,second-order 的函數空間也由 context indexing 轉換成 first-order。因此得到一個有 some “correctness by construction” properties 的 GAT,比如每個操作都自動保留替換。這對複雜的理論來說,如果不是從 SOGAT 出發而是直接用其 GAT 表示,那這種屬性並不 trivial。
Cubical type theory 跟有 internal parametricity 的 type theory 都可以定義成 SOGATs,這些方法已經用來證明型別論的屬性。
Substructural (像是 linear or modal) type theories 無法用這篇論文說的方法用 SOGATs 定義,但有時候 presheaves over a substructural theory 提供的 substructural internal language 可以用來描述理論,像是 multi-modal type theory。
簡單的代數理論可以用 signatures 和方程式來表示,也可以 presentation independently 為 Lawvere theories。
GATs 的 syntactic signatures 可以用 preterms 跟 well-formedness relations 定義,也可以 presentation-independent 為 contextual categories 或 categories with families (CwFs) 或 clans。
GATs 的 theory of signatures (ToS) 方法落在 syntactic 跟 presentation-independent 方法中間:signatures 用某個 GAT 語法定義,這是一種設計來專用於定義簽名的類型理論。簽名跟我們在 Agda 裡寫下的 inductive datatype 定義一模一樣:A list (telescope) of the curried types of sorts and constructors。ToS 裡一個 signature 是一個理論的具體表示,但在 well-typed quotiented syntax 這層抽象上給出。這讓我們得到優雅的語意構造,又還是能用 signatures 工作。
SOGATs 同樣可以定義成 syntactically 或 presentation-independently(用 representable map categories 或是 CwFs with locally representable types)
這篇論文貢獻了 ToS 風格的 SOGATs 定義。SOGAT signatures 的理論本身也是 SOGAT,所以這個理論可以描述自己。
避免了循環論證,因為我們首先將 SOGAT 簽名定義為 GAT,從而引導 SOGAT 簽名理論,而 GAT 簽名理論(即 GAT 的語法)本身可以使用 Church 編碼進行引導。
Contributions [local-2]
Contributions [local-2]
The main takeaway of this paper is that structural languages are SOGATs.
We justify this claim through several examples. Our technical contributions are the following:
- The theory of SOGAT signatures (ToS+), a domain-specific type theory in which every closed type is a SOGAT signature. As it is a structural type theory, it can be defined as a SOGAT itself. Signatures can be formalised in ToS+ without encoding overhead.
- A translation from SOGAT signatures to GAT signatures based on a parallel substitution calculus. Thus, for every SOGAT, we obtain all of the semantics of GATs: a category of models with an initial object, (co)free models, notions of displayed models and sections, the fact that induction is equivalent to initiality, and so on. The GAT descriptions that we obtain are readable, do not contain occurrences of Yoneda as in usual presheaf function spaces. Correctness of the translation is showed by proving that internally to presheaves over a model of the GAT, a second-order model of the SOGAT is available.
- We define an alternative translation producing a single substitution calculus.
作者開始展示如何把各種 logic 或程式語言定義成代數理論。這邊我寫下每個代數理論的 agda 版本
Schönfinkel's combinator calculus (Algebraic Theories) [ag-0003]
Schönfinkel's combinator calculus (Algebraic Theories) [ag-0003]
{-# OPTIONS --safe --without-K #-} module ag-0003 where open import MLTT.Spartan
Combinator calculus 可以看成一個代數理論,這時候它有
- 一個 sort of terms
- 一個 binary
- 兩個 nullary operations
- 兩個等式
record combinator-calculus : 𝓤₁ ̇ where field Tm : 𝓤₀ ̇ _·_ : Tm → Tm → Tm K : Tm S : Tm Kβ : {u f : Tm} → K · u · f = u Sβ : {f g u : Tm} → S · f · g · u = f · u · (g · u) infixl 30 _·_
- 從這個符號可以明顯看出代數/模型的概念
- Combinator calculus 的 quotiented syntax 是初始模型,它總是存在。
- Notions of homomorphism, displayed/dependent model, induction, products and coproducts of models, free models, and so on, are derivable from the signature, as described in any book on universal algebra
- Algebraic Theory 的 initial algebra 叫做 quotient inductive type
其他 single-sorted algebraic theories 著名案例:
- 邏輯:經典(或直覺主義)命題邏輯,定義為布林代數(或海廷代數)理論
- 代數:monoids、群、環、lattices 等等
Generalised algebraic theories (GATs) [local-3]
Generalised algebraic theories (GATs) [local-3]
Generalised algebraic theories (GATs) 的 sort 可以 indexed by 其他 sort。案例有 typed combinator calculus、propositional logic with Hilbert-style proof theory、theories of graphs、preorders、categories 等等
Typed combinator calculus (Generalised algebraic theories) [ag-0004]
Typed combinator calculus (Generalised algebraic theories) [ag-0004]
{-# OPTIONS --safe --without-K #-} module ag-0004 where open import MLTT.Spartan
record typed-combinator-calculus : 𝓤₁ ̇ where field
給 types 的 sort
Ty : 𝓤₀ ̇
每個 type 對應(index)一個 term 用的 sort
Tm : Ty → 𝓤₀ ̇ ι : Ty _⇒_ : Ty → Ty → Ty _·_ : {A B : Ty} → Tm (A ⇒ B) → Tm A → Tm B K : {A B : Ty} → Tm (A ⇒ B ⇒ A) S : {A B C : Ty} → Tm ((A ⇒ B ⇒ C) ⇒ (A ⇒ B) ⇒ A ⇒ C) Kβ : {A B : Ty} {u : Tm A} {f : Tm B} → K · u · f = u Sβ : {A B C : Ty} {f : Tm (A ⇒ B ⇒ C)} {g : Tm (A ⇒ B)} {u : Tm A} → S · f · g · u = f · u · (g · u) infixl 40 _·_ infixr 30 _⇒_
上述 Algebraic Theory 的通用代數特徵可以推廣到 GAT。具體來說,每個 GAT 都具有由 quotient inductive-inductive type 給出的語法,我們有 free 模型和 cofree 模型。
Second-order algebraic theories (SOATs) [local-4]
Second-order algebraic theories (SOATs) [local-4]
如果一個語言有變數或是綁定,就被定義成一個二階理論。
Lambda calculus (Second-order algebraic theories) [ag-0005]
Lambda calculus (Second-order algebraic theories) [ag-0005]
{-# OPTIONS --safe --without-K #-} module ag-0005 where open import MLTT.Spartan
record lambda-calculus : 𝓤₁ ̇ where field Tm : 𝓤₀ ̇
lam 的(metatheory)型別不是一階的(not strictly
positive)
lam : (Tm → Tm) → Tm _·_ : Tm → Tm → Tm β : {f : Tm → Tm} {u : Tm} → lam f · u = f u infixl 30 _·_
By the syntax of lambda calculus, we mean the syntax for the GAT of Definition 4. However, we still prefer to define lambda calculus as a SOGAT: it is a shorter definition, does not include boilerplate, and ensures that once translated to its first-order version, all operations respect substitution by construction.
此外,我們可以像邏輯框架一樣,使用二階表示來進行程式設計。這意味著,使用二階表示,我們可以定義 derivable operation 並證明 derivable 等式,而不是像證明 admissible 那樣需要歸納法。
舉例來說 Y combinator 是 derivable operation。可以證明它是 fixpoint combinator:
Y : Tm Y = lam (λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) Y-is-fixed-point : {f : Tm} → Y · f = f · (Y · f) Y-is-fixed-point {f} = Y · f =⟨by-definition⟩ lam (λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) · f =⟨ β ⟩ (λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) f =⟨ refl ⟩ (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x))) =⟨ β ⟩ f · ((lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) =⟨ refl ⟩ f · ((λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) f) =⟨ ap (f ·_) (β ⁻¹) ⟩ f · (Y · f) ∎
這種推理對任何 second-order model 都有效,而且任何 first-order model 都可以在 internal language of presheaves over first-order model 裡被升級成 second-order model。
但注意沒有可用的 SOAT models 和 之間的同態概念。為了討論同態或語法,我們將 SOAT 轉換為一階 GAT:加上上下文、替換、索引 Tm 以及所有基於上下文的操作,然後 lam 就變成了一個以擴展上下文中的項作為輸入的一階函數。轉換出來的 GAT 就是
Lambda calculus (GAT) [ag-0006]
Lambda calculus (GAT) [ag-0006]
{-# OPTIONS --safe --without-K #-} module ag-0006 where open import MLTT.Spartan hiding (_∘_; id)
作者這邊開始解釋從二階理論得出一階理論(GAT)的標準過程
record first-order-lambda-calculus : 𝓤₁ ̇ where field Con : 𝓤₀ ̇ Sub : Con → Con → 𝓤₀ ̇
有 terminal object 的 category
_∘_ : {Δ Γ Θ : Con} → Sub Δ Γ → Sub Θ Δ → Sub Θ Γ assoc : {A B C D : Con} {γ : Sub C D} {δ : Sub B C} {θ : Sub A B} → (γ ∘ δ) ∘ θ = γ ∘ (δ ∘ θ) id : {Γ : Con} → Sub Γ Γ id-left : {A B : Con} {γ : Sub A B} → id ∘ γ = γ id-right : {A B : Con} {γ : Sub A B} → γ ∘ id = γ -- empty context: zero ◇ : Con ε : {Γ : Con} → Sub Γ ◇ -- terminal ◇η : {Γ : Con} → (σ : Sub Γ ◇) → σ = ε
sort Tm 現在 indexed by Con 且有一個
instantiation operation,這個 operation 是 functorial
([◦], [id]).
Tm : Con → 𝓤₀ ̇ _[_] : {Γ Δ : Con} → Tm Γ → Sub Δ Γ → Tm Δ [id] : {Γ : Con} {t : Tm Γ} → t [ id ] = t [∘] : {Θ Γ Δ : Con} {t : Tm Γ} {γ : Sub Δ Γ} {δ : Sub Θ Δ} → t [ γ ∘ δ ] = t [ γ ] [ δ ]
context extension 讓 contexts 是 natural number algebra
_▹ : Con → Con
substitutions 是一串 terms,由組成元件表達
_,,_ : {Δ Γ : Con} → Sub Δ Γ → Tm Δ → Sub Δ (Γ ▹)
有了 contexts 跟 substitutions,變數就可以定義成 De Bruijn indices:
0 = q1 = q[p]2 = q[p] [p],以此類推
p : {Γ : Con} → Sub (Γ ▹) Γ q : {Γ : Con} → Tm (Γ ▹)
應該滿足的等式規則
▹β₁ : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm Δ} → p ∘ (γ ,, t) = γ ▹β₂ : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm Δ} → q [ γ ,, t ] = t ▹η : {Δ Γ : Con} {σ : Sub Δ (Γ ▹)} → σ = (p ∘ σ ,, q [ σ ]) lam : {Γ : Con} → Tm (Γ ▹) → Tm Γ lam[] : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm (Γ ▹)} → (lam t)[ γ ] = lam (t [ γ ∘ p ,, q ]) _·_ : {Γ : Con} → Tm Γ → Tm Γ → Tm Γ ·[] : {Δ Γ : Con} {γ : Sub Δ Γ} {t u : Tm Γ} → (t · u)[ γ ] = t [ γ ] · (u [ γ ]) β : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm (Γ ▹)} {u : Tm Γ} → lam t · u = t [ id ,, u ] infixl 40 _∘_ infixl 30 _,,_ infixl 40 _·_ infixl 50 _[_]
Second-order generalised algebraic theories (SOGATs) [local-5]
Second-order generalised algebraic theories (SOGATs) [local-5]
SOGATs combine the two previous classes: sorts can be indexed over previous sorts and second-order operations are allowed.
Simply typed lambda calculus [ag-0007]
Simply typed lambda calculus [ag-0007]
{-# OPTIONS --safe --without-K #-} module ag-0007 where open import MLTT.Spartan open import UF.Equiv
record simply-typed-lambda-calculus : 𝓤₁ ̇ where field Ty : 𝓤₀ ̇ _⇒_ : Ty → Ty → Ty
generalised 的部分是因為 index Tm by Ty
Tm : Ty → 𝓤₀ ̇
綁定的部分
lam : {A B : Ty} → (Tm A → Tm B) → Tm (A ⇒ B) _·_ : {A B : Ty} → Tm (A ⇒ B) → (Tm A → Tm B) stlc-cong : {A B : Ty} → Tm (A ⇒ B) ≃ (Tm A → Tm B)
一樣參照 first-order lambda calculus 的過程,加上 contexts、加上 substitutions,相應的 first-order 等式跟改寫,就會得到 simply-typed-lambda-calculus 的 GAT。
Minimal intuitionistic first-order logic (SOGAT) [ag-0008]
Minimal intuitionistic first-order logic (SOGAT) [ag-0008]
{-# OPTIONS --safe --without-K #-} module ag-0008 where open import MLTT.Spartan open import UF.Subsingletons
record minimal-intuitionistic-first-order-logic : 𝓤₁ ̇ where field For : 𝓤₀ ̇ Tm : 𝓤₀ ̇ _⊃_ : For → For → For All : (Tm → For) → For Eq : Tm → Tm → For Pf : For → 𝓤₀ ̇ Pf-is-prop : (A : For) → is-prop (Pf A) intro⊃ : {A B : For} → (Pf A → Pf B) → Pf (A ⊃ B) elim⊃ : {A B : For} → Pf (A ⊃ B) → (Pf A → Pf B) intro∀ : {A : Tm → For} → ((𝑡 : Tm) → Pf (A 𝑡)) → Pf (All A) elim∀ : {A : Tm → For} → Pf (All A) → ((𝑡 : Tm) → Pf (A 𝑡)) introEq : {t : Tm} → Pf (Eq t t) elimEq : {t t' : Tm} → (A : Tm → For) → Pf (Eq t t') → Pf (A t) → Pf (A t')
一樣參照 first-order lambda calculus 的過程,加上 contexts、加上 substitutions,相應的 first-order 等式跟改寫。
Polymorphic lambda calculus (SOGAT) [ag-0009]
Polymorphic lambda calculus (SOGAT) [ag-0009]
{-# OPTIONS --safe --without-K #-} module ag-0009 where open import MLTT.Spartan
record polymorphic-lambda-calculus : 𝓤₁ ̇ where field Ty : 𝓤₀ ̇ Tm : Ty → 𝓤₀ ̇ _⇒_ : Ty → Ty → Ty lam : {𝐴 𝐵 : Ty} → (Tm 𝐴 → Tm 𝐵) → Tm (𝐴 ⇒ 𝐵) _·_ : {𝐴 𝐵 : Ty} → Tm (𝐴 ⇒ 𝐵) → (Tm 𝐴 → Tm 𝐵) All : (Ty → Ty) → Ty Lam : {𝐴 : Ty → Ty} → ((𝑋 : Ty) → Tm (𝐴 𝑋)) → Tm (All 𝐴) _•_ : {𝐴 : Ty → Ty} → Tm (All 𝐴) → ((𝑋 : Ty) → Tm (𝐴 𝑋))
一樣參照 first-order lambda calculus 的過程,加上 contexts、加上 substitutions,相應的 first-order 等式跟改寫。
System Fω (SOGAT) [ag-000A]
System Fω (SOGAT) [ag-000A]
{-# OPTIONS --safe --without-K #-} module ag-000A where open import MLTT.Spartan
record system-F-ω : 𝓤₁ ̇ where field □ : 𝓤₀ ̇ Ty : □ → 𝓤₀ ̇ _⇛_ : □ → □ → □ LAM : {K L : □} → (Ty K → Ty L) → Ty (K ⇛ L) _●_ : {K L : □} → Ty (K ⇛ L) → (Ty K → Ty L) ∗ : □ Tm : Ty ∗ → 𝓤₀ ̇ All : {K : □} → (Ty K → Ty ∗) → Ty ∗ Lam : {K : □}{A : Ty K → Ty ∗} → ((X : Ty K) → Tm (A X)) → Tm (All A) _•_ : {K : □}{A : Ty K → Ty ∗} → Tm (All A) → ((X : Ty K) → Tm (A X)) _⇒_ : Ty ∗ → Ty ∗ → Ty ∗ lam : {A B : Ty ∗} → (Tm A → Tm B) → Tm (A ⇒ B) _·_ : {A B : Ty ∗} → Tm (A ⇒ B) → (Tm A → Tm B)
System Fω 轉換後有
- 3 個 operations 綁定 Ty-variables
- 1 個 operation 綁定 term-variable
Minimal Martin-Löf type theory (SOGAT) [ag-000B]
Minimal Martin-Löf type theory (SOGAT) [ag-000B]
{-# OPTIONS --safe --without-K #-} module ag-000B where open import MLTT.Spartan open import MLTT.NaturalNumbers
variable 𝑖 : ℕ record minimal-martin-lof-type-theory : 𝓤₁ ̇ where field Ty : ℕ → 𝓤₀ ̇ U : (𝑖 : ℕ) → Ty (succ 𝑖) Tm : Ty 𝑖 → 𝓤₀ ̇ c : Ty 𝑖 → Tm (U 𝑖) El : Tm (U 𝑖) → Ty 𝑖 PI : (A : Ty 𝑖) → (Tm A → Ty 𝑖) → Ty 𝑖 Lift : Ty 𝑖 → Ty (succ 𝑖) lam : {𝐴 : Ty 𝑖}{𝐵 : Tm 𝐴 → Ty 𝑖} → ((𝑎 : Tm 𝐴) → Tm (𝐵 𝑎)) → Tm (PI 𝐴 𝐵) _·_ : {𝐴 : Ty 𝑖}{𝐵 : Tm 𝐴 → Ty 𝑖} → Tm (PI 𝐴 𝐵) → ((𝑎 : Tm 𝐴) → Tm (𝐵 𝑎)) mk : {𝐴 : Ty 𝑖} → Tm 𝐴 → Tm (Lift 𝐴) un : {𝐴 : Ty 𝑖} → Tm (Lift 𝐴) → Tm 𝐴
這個理論的對應 GAT
得到一個具有族的範疇(CwF),更準確地說,是一個具有 N 個 families
的範疇,這些族配備了 familywise Π-types、宇宙以及族之間的一步向上提升。
這些類型是 Ty : Con → N → Set 和
Tm : (Γ : Con) → Ty Γ 𝑖 → Set,其中 𝑖
論證隱含在後者中。
後面幾節
- 第三節 Theories of signatures as SOGATs,開始把 signatures 理論也寫成 SOGAT 來討論
- 第四節 Naive semantics of SOGAT signatures,討論 for any SOGAT signature 的 a notion of first-order model.
- 第五節 Direct semantics of SOGAT signatures,用一個更小心版本的 presheaf model 定義 first-order models of SOGATs
- 第六節 GAT signature semantics of SOGAT signatures,把 SOGAT signatures 轉成 GAT signatures 的方法
Intrinsically typed term [ag-0002]
Intrinsically typed term [ag-0002]
{-# OPTIONS --safe --without-K #-} module ag-0002 where open import MLTT.Spartan hiding (Type) open import MLTT.List
Type 在 STLC 還只需要是一個簡單的 formation
data Type : 𝓤₀ ̇ where bool : Type _⇒_ : Type → Type → Type infixr 50 _⇒_ variable S T : Type
Context 通常會自訂,比如 MLTT 需要兩種綁定時自訂就會更方便一些
Ctx = List Type _▷_ : Ctx → Type → Ctx Γ ▷ T = T ∷ Γ infix 40 _▷_ variable Γ : Ctx
Intrinsically-scoped de Brujin indices
基本上變數都長這樣
data _∋_ : Ctx → Type → 𝓤₀ ̇ where here : Γ ▷ T ∋ T there : Γ ∋ T → Γ ▷ S ∋ T infix 20 _∋_ variable x : Γ ∋ T
Intrinsically-typed terms
確保 term 是類型良好的一種方式就是從一開始就跟 context 一起構造,讓 terms 必須是 well-typed
data _⊢_ : Ctx → Type → 𝓤₀ ̇ where true false : Γ ⊢ bool var : Γ ∋ T → Γ ⊢ T lam : Γ ▷ S ⊢ T → Γ ⊢ S ⇒ T _·_ : Γ ⊢ S ⇒ T → Γ ⊢ S → Γ ⊢ T if_then_else_ : Γ ⊢ bool → Γ ⊢ T → Γ ⊢ T → Γ ⊢ T infix 30 _⊢_
Video. Why You Can't Bring Checkerboards to Math Exams [math-001E]
Video. Why You Can't Bring Checkerboards to Math Exams [math-001E]
A cool way to do multiply, divide and root!
Definition. Diffeological space [math-001D]
Definition. Diffeological space [math-001D]
A diffeological space is a pair consists of a given set and a diffeology consists of a collection of parameterizations satisfying the following conditions:
- All parameterizations with domain belong to , namely all the points of
- If is a parameterization, and is a smooth map between cartesian spaces, then belongs to
- If is a parameterization, an open cover of that each restriction , then
If is a diffeology, then we call a parameterization that belongs to it a plot.
Lemma. Presheaves are colimits of representables [math-001B]
Lemma. Presheaves are colimits of representables [math-001B]
The presheaf is the colimit of the functor ,
Broken pipe (os error 32)where is the yoneda embedding, is the category of elements of . For morphism .
Proof. [local-0]
Proof. [local-0]
We first show that is a cocone, for each object , there is a morphism
here abuse notation that has a corresponding in because the Yoneda lemma.
and for each , the following diagram commutes
hence is a cocone. Given any other cocone , which means a collection of sections
where for each by definition. The point is if we define a natural transformation
Broken pipe (os error 32)naturality follows because implies . It is clear that is the unique natural transformation under , showing that is the colimit.
Presheaves, Yoneda embedding, and Yoneda lemma [math-001A]
Presheaves, Yoneda embedding, and Yoneda lemma [math-001A]
Definition. Presheaf [local-0]
Definition. Presheaf [local-0]
Let be a category. A presheaf over is a functor of the form
For each object , we will denote by
the evaluation of at . The set will sometimes be called the fibre of the presheaf at , and the elements of thus deserve the name of sections of over .
For morphism , the induced map from denotes .
The category of presheaves over denotes .
Definition. Yoneda embedding [local-1]
Definition. Yoneda embedding [local-1]
Yoneda embedding is a functor
we denote
Lemma. Yoneda [local-3]
Lemma. Yoneda [local-3]
For any presheaf over , there is a natural bijection of the form
Proof. [local-2]
Proof. [local-2]
We first define inverse map , given a section of over , i.e. , we have
for each morphism . This indeed defines a morphism in .
Now check and indeed are inverse of each other. First: given , we have
Another direction: given , we have
for each . Naturality is obvious, hence they form a natural bijection.
隱式編程:coherence 與 stability 屬性 [tt-000T]
隱式編程:coherence 與 stability 屬性 [tt-000T]
這篇是 COCHIS: Stable and coherent implicits 的筆記
隱式編程機制是指,使用型別指導的推導能力,在使用者不提供完整資訊的情況下給出程式語意的技術。比如 Haskell 的 type class、Rust 的 trait 等。合成的過程叫做 resolution。
Haskell 的 type class 的一個重要特徵是給定的類型只會有一個 instance 符合。coherence 在這個意義下指的是,給出的程式語意是唯一的,也就是說對某段合法程式碼,不會合成出超過一個語意。
比如説 Haskell 會拒絕 show (read "3") == "3" 這段程式碼,因為根據 type class resolution 有很多種可能性(show : α -> String 跟 read : String -> α)
- 選了
α := Float那結果是False,因為show (read "3") == "3.0" - 選了
α := Int那結果是True - 選了
α := Char那結果是True
所以這種會導致有多種語意出現的程式就需要被拒絕。
Haskell 的 overlapping instances 技術是對上述問題的一種推廣(使我們可以接受更多程式),比如說
class Trans α where trans :: α → α instance Trans α where trans x = x instance Trans Int where trans x = x + 1
對於程式 trans 3 應該要決定出什麼結果?Overlapping 的決定是,因為 α := Int 比沒有決定更特定,因此選 instance Trans Int。然而,也有 overlapping 策略也無法決定的情況,比如下面比較刻意的
class C α β where m :: α → β → Bool instance C Bool α where mx y = x instance C α Bool where mx y = y
對程式 m True False 兩個 instances 都一樣特定,沒辦法決定,因此這段程式碼也必須被拒絕。
Stability 是跟 coherence 高度相關的屬性。不正式的說,stable 是指 type variables 的實例化與否不影響 resolution 的結果。但 overlapping 技術會影響這個結果,比如
bad :: α → α bad x = trans x
就是一個 unstable 的定義。如果寫成 Trans α => α → α 就不一樣了,這表示 α 交由呼叫 bad 的地方決定,但這裡則是必須在定義處馬上決定,如果 Haskell 接受這段定義,那可能會選擇第一個 instance Trans,導致 bad 3 是 3 而 trans 3 是 4。雖然 bad x := trans x 是定義等價。
也可以參考 https://blog.ezyang.com/2014/07/type-classes-confluence-coherence-global-uniqueness/ 的案例跟論點。
Definition. 流形上的微分式 [math-0019]
Definition. 流形上的微分式 [math-0019]
設 為 differentiable manifold 的局部座標,可以把微分式定義為 的對偶基底,記為 。亦即
一階微分式的整體記為 。
任何給定的微分式 可以寫成向量形式
對一個 ,什麼是 ?用向量微積分的觀點,是函數 的一階變化量
因此其類型是 的線性函數,通過空間對偶可知這就是 的元素。
性質一
證明如下:設
又有
因此
然而要注意到,並不是每個 都可以表示成某個 的微分 。
性質二
而且,對於每個具體的 , 顯然是一種 的特例,因此也可以定義
驗證
可見如此定義的 跟取對偶基底的結果相同。
Definition. 切向量場沿曲線平行 (parallel) [math-0018]
Definition. 切向量場沿曲線平行 (parallel) [math-0018]
令 為一 -affine manifold 上一 -曲線。 為 上有意義的切向量場(i.e. 對所有 ,可以對 可微的指定一個 )
稱 沿 為平行。
若適當的局部座標為 ,則
Broken pipe (os error 32)令 (即速度向量),則
因此
因此
沿 平行的充要條件為滿足一階線性方程組
測地線方程組推導 [math-0017]
測地線方程組推導 [math-0017]
令 為一 -affine manifold 上一 -曲線,我們定義當
對所有 成立時, 為一測地線。只要參考切向量場沿著某一曲線如何被視為平行定義的推廣就可以直觀的看出測地線的幾何意義。
藉由座標 ,可將 表達為
故推導當 為一測地線時,有方程式
因此測地線方程組就是指
The Basel problem with trigonometric Fourier series [math-0016]
The Basel problem with trigonometric Fourier series [math-0016]
An idea is define on . Its trigonometric Fourier series was:
which is periodic and converges to in .
Observing that is even, hence
for all . Now compute
and each is
Now let's focus on integral by part
and again
It seems complicated, but in fact we have , hence we can ignore them in this definite integral
Therefore, if we compute can get
Hence
Broken pipe (os error 32)Definition. Impredicative [tt-000V]
Definition. Impredicative [tt-000V]
參考 https://github.com/AndrasKovacs/elaboration-zoo/tree/master/06-first-class-poly
In type theory
A universe is impredicative if function types whose codomains are in the universe are always in the universe, regardless of their domain types.
如果 可以通過檢查,這個 Universe 就是 impredicative 的,有 impredicative universe 存在的類型理論就叫做有 impredicativity。像 Rocq 或是 Lean 都有特殊的 Prop universe 有這樣的特性。
In Elaboration algorithm
An elaboration algorithm is impredicative if it is able to solve metavariables to implicit function types.
is diffeomorphic to [math-0015]
is diffeomorphic to [math-0015]
Construction
- and
- and
and use
- and
- and
The diffeomorphism defined as
Given we have a ratio , we want to recover a point on , how to get this inverse map? The idea is
Broken pipe (os error 32)Now we can use quadratic formula to solve (and remind that ):
Broken pipe (os error 32)However, hence
By this we can see
Therefore, is
The similiar reasoning can show
Hence, for (i.e. ) we have
By component, first check :
Broken pipe (os error 32)Then check :
Broken pipe (os error 32)So is indeed well defined, and smooth on it domain, the inverse defined as
where and because the equivalence. These maps are smooth on and agree each other (inverse the ratio because the position) when meet hence well defined. Hence is a diffeomorphism.
Proposition. is open [math-4M36]
Proposition. is open [math-4M36]
Let the set of those lines that intersect .
Proof. [local-0]
Proof. [local-0]
By definition, is open if and only if its preimage in is open (its preimage under the map ).
Hence, we want to prove is open in . Because , and inherits the topology of , so if we can show an open set such that , then is an open set. Then we can see if we define , it's open and , so is open in and is open in .
Definition. Real Projective -space as quotient of [math-UGKQ]
Definition. Real Projective -space as quotient of [math-UGKQ]
Another famous view is viewing as the quotient of the sphere , because it’s obvious that each element (a line) of projective -space intersects exactly two points, and the two points are antipodal points!
Use to represent an element of that intersects at .
Therefore, if we make a quotient relation:
Then we can see that , this homeomorphism can be used to transfer the -structure on to .
Definition. Jacobian matrix [math-0014]
Definition. Jacobian matrix [math-0014]
Let be a map, hence we can view each component is a function :
with respect to standard bases, and , is given by the matrix of partial derivatives (the Jacobian matrix) in the following sense
Or using the index notation, so can be expressed as:
Type system 的 Soundness 與 Completeness [tt-000S]
Type system 的 Soundness 與 Completeness [tt-000S]
我們說型別系統 sound 的時候,意思是如果一隻程式的型別不正確,系統就不會接受這隻程式。這蘊含了如果程式被系統接受 (type-checked),那就一定是沒有類型錯誤的程式。
我們說型別系統 complete 的時候,意思是如果一隻程式的型別正確,就一定會被系統接受。
我們通常更偏好滿足 soundness,因為有型別錯誤卻被接受的程式,因為比起有幾個需要改寫幾隻程式的麻煩,unsound 往往能造成更大的問題。
Definition. Predicative [tt-000R]
Definition. Predicative [tt-000R]
Counterexamples in Type Systems
A type system is predicative if definitions can never be referred to, even indirectly, before they are defined.
Definition. Injectivity [tt-000Q]
Definition. Injectivity [tt-000Q]
Counterexamples in Type Systems
如果我們說一個型別建構子 是 Injective,那麼意思是如果 則 。
一個程式語言的各個參數化型別不必然都具有這個特性。
代數幾何:非常基本的部分 [math-XGSJ]
代數幾何:非常基本的部分 [math-XGSJ]
代數幾何的核心物件是:多個多項式等式構成的系統
- 有 個變數,記為
- 有 個多項式
幾何上我們就是研究 中解集的軌跡。代數上我們就是研究
這個 algebra。事實上任何有限生成 ring 都可以表示成這個形式: finitely generated 表示存在一個 surjective map ,然後 Hilbert Basis theorem 說明這個 map 的 kernel 可以用有限個元素生成。
這個理想是由 linear combinations 的形式組成的,其中 是多項式
Definition. maximal ideal [math-0013]
Definition. maximal ideal [math-0013]
A maximal ideal of a commutative ring is a proper ideal of such that, whenever is an ideal of and , then or .
An equivalent condition is is a field if and only if is maximal.
Definition. prime ideal [math-0012]
Definition. prime ideal [math-0012]
Let be a ring and be an ideal, the followings are equivalent conditions to say that is prime
- is prime if than or for all
- is prime if is an integral domain
Proof
Backward
Let be an integral domain, that's say if and , then or . Let be the zero element of (i.e. ), then . Hence or , implies or .
Forward
Let be a prime ideal, let
then and therefore, or . Hence or is the zero coset in .
Algorithm. 君主選舉 [cs-000I]
Algorithm. 君主選舉 [cs-000I]
前提
- 每個節點入場的時候都分配到一個代數(generation),這個數字是唯一的
- 第一個啟動節點直接當選
當原始的領導者掛了(一段時間無回應),注意到這點的節點就開始問比自己老的所有節點是不是還活著
- 收到 alive 回應,或是得到其他更高優先順序的候選節點資訊。
- 從中選出最老(代數數字最小)的節點告知它當選了,當選節點會廣播自己當選的消息。
問題
- 注意到領導者無回應而發起投票的節點可以超過一個
- 兩個發起投票的節點有連線的節點當然可能不同
比如 5 6 都注意到 1 死亡,發起投票。3 4 跟 5 有連線於是選出 2;2 3 跟 6 有連線於是選出 3。這時候 2 3 就都覺得自己是領導者了,而且 5 對 6 的通知還是更不正確的結果。
當然補上當選節點廣播之後,較年輕的當選者會自己去除這個屬性也是可以,但這中間會有一小段時間可能發生(以資料庫而言)雙重寫入而遺失資料。
而且要注意到實際上當然可以比這麻煩的多,比如通訊密集時,更容易讓 leader 過載;同時 90% 的節點都發現這點並發起投票,那麼消除腦分裂前的混亂就會特別嚴重。
Internal language 之用 [math-0011]
Internal language 之用 [math-0011]
這是 An informal introduction to topos theory 的閱讀筆記,Leinster 在這裡說 generalized elements 可以說是 Category 的 internal language。而 set theoretic 裡面使用 element 的論證多半都能改用這樣的語言進行,甚至,不使用 LEM 與 AC 的構造式證明,可以在任意 topos 中使用。
除了在 Generalized element 已經討論過的 product ,topos 還有 exponentials ,equalizer 也可以記為
表示 。
這樣就無需使用大量的 diagram,而是採用數學家已經熟悉的集合式的論證即可。
Definition. Generalized element [math-0010]
Definition. Generalized element [math-0010]
Let be a category, and let be an object of . A generalized element of is simply a map in with codomain .
A generalized element is shape or -element of .
When (the terminal) then -elements are called global elements.
Global elements can be very boring, for example in the category of groups.
The language of generalized elements is the internal language of the category. For example, let be a category with finite products. An -element of consists of two component and is denoted by , hence extended the notation of set-theoretic Cartesian product of global elements.
Definition. Immersion, embedding, and submanifold [math-000Z]
Definition. Immersion, embedding, and submanifold [math-000Z]
Let be differentiable manifolds (dimensions are and respectively). A differentiable map is said to be an immersion if
is injective for all .
If in addition, is a homeomorphism onto , where has the subspace topology induced from , then is an embedding.
If and the inclusion is an embedding, then is a submanifold of .
Proposition. Right adjoint fully faithful <=> counit is isomorphism [math-000Y]
Proposition. Right adjoint fully faithful <=> counit is isomorphism [math-000Y]
Suppose is an adjunction, and is fully faithful, then counit is an isomorphism
Proof
Forward direction
To prove counit is an isomorphism, we need to find an inverse and show pre and post composition of them are identity. Let , then we have two targets
-
Apply to get
hence the target is , right triangle fills the target.
-
Use counit naturality on to get
Therefore, we have target , left triangle fills the target.
Backward direction
For is faithful, we want to know if then . We first obtain two equations via naturality of counit:
Replace with then we have , counit is an isomorphism and hence left-cancellable, .
For is full, we want to show every there is a such that . Let (where is the hom-set equivalence of adjunction), this is same as asking
because isomorphism property, we have
now we use isomorphism to cancel right, so .
Counterexample. no need to be identity when [math-000X]
Counterexample. no need to be identity when [math-000X]
The counterexample in the category of sets is
We have for all , but is not identity. Where represent the set with and elements, respectively.
tr-notes transclude 的發展 [tr-0007]
tr-notes transclude 的發展 [tr-0007]
tr 最開始我的想法是讓每一張卡片自己都輸出一個 HTML 網頁,然後就想到「哎糟糕,被嵌入 (transclude 概念) 的網頁會有重複的共用元素」就放棄了,當時認為所以必須像 forester 那樣用 XML 才行
好久以後我再次考慮(2025/05)實現一個 forester fork 時才想到,只要每張卡生成一個 a.index.html 一個 a.embed.html 就可以避免重複元素了
順著這個想法我用 iframe 嵌入來實現功能,直到我實在解不開 JS 的工作空間問題,這逼我思考其他方案。結果過了幾天我想到其實根本不用這麼麻煩xd,transclude 直接讀 embed 的內容就好了(並且 escape 排版確保不破壞 pre tag 等對排版敏感的內容)
現在剩下的問題就是其實 index 其實也沒必要再用 racket 生成一次,而是應該把 header, footer 等內容插入,讀取自己的 embed 檔案,但目前耦合比較多(依靠 generate-index? 判斷是否生成這些區塊),需要重新思考怎麼編排這些程式
魔物獵人荒野 充能斧 操作筆記 [game-0000]
魔物獵人荒野 充能斧 操作筆記 [game-0000]
基本操作
- △: 劍 牽制斬
- △ + O: 劍 突進斬
- O 長按: 劍 蓄力上撈斬
- R2 + △: 劍 變形斬
- R2 + O: 劍 充能
強化瓶系統
最有效率的集氣連技是: O 長按 → △
但魔物太靈活時這樣可能會一直落空,不一定要堅持這樣打
充能模式
1. 充能盾牌(紅盾)
架盾操作:- R2 + O 之後保持 O 不放開
- △ + O 三次接 R2
- 突進斬
- 盾突刺
- 高解
- 屬性強化迴旋斬
2. 充能劍(紅劍)
操作流程:- R2 + O 後按住 △ 進行蓄力
- 放開後打出「劍:高壓屬性斬」
3. 充能斧(紅斧)
觸發條件有三種(任何一個達成就會觸發紅斧模式):- L2 瞄準用 R1 集中攻擊打到傷口(必須命中才會觸發)
- 精準防禦之後按 △
- 騎乘打出處決後觸發
出紅斧是為了能長按攻擊鍵 △ 或是 O 時,斧會持續輸出而不是只有一次輸出
Proposition. Christoffel 等於 0 iff g 是常數(平直空間) [math-GDOS]
Proposition. Christoffel 等於 0 iff g 是常數(平直空間) [math-GDOS]
Christoffel 定義為
Proof. [local-0]
Proof. [local-0]
(<=) 是常數表示微分為 ,因此 Christoffel
(=>) 因為
對兩邊取積分可知
Naturality cannot be given by a family of isomorphisms [math-000S]
Naturality cannot be given by a family of isomorphisms [math-000S]
This is came from when I'm formalizing lemma 1.3.11 of Basic Category Theory, I miss a precondition ( below must be a natural transformation in the lemma) and try to prove an impossible thing.
Let be functors, and a family
Does must be natural?
Counterexample. [math-000T]
Counterexample. [math-000T]
The result is can be not natural.
This counterexample is given by Zhixuan Yang:
Let be the two-object one-arrow category, and be , and
where is the two elements set. For we choice and , then is not natural.
Definition. exterior algebra [math-000R]
Definition. exterior algebra [math-000R]
The exterior algebra of vector space is defined as a -graded algebra:
Definition. Homotopy extension property (HEP) [math-000O]
Definition. Homotopy extension property (HEP) [math-000O]
A map of spaces has the homotopy extension property for a space if
- for each homotopy
- and for each map with for all
there is a homotopy such that
for all , and . The idea can be expressed in the following commutative diagram:
The homotopy is called the extension of with initial condition .
Definition. Natural Transformation [math-000N]
Definition. Natural Transformation [math-000N]
Let and be categories, let be functors. A natural transformation is a function consists of
- For each , there is a morphism in , called the -component of
- For every morphism in , there is a commute diagram
常青筆記的困難 [note-0001]
常青筆記的困難 [note-0001]
Sterling 的 https://www.forester-notes.org/QHXX/index.xml 精確的描述了常青筆記可能遭遇的困難,關鍵在於,常青筆記對於不停變化的目標,如數學、電腦程式框架等存在,本體論的目標並不統一。用數學為例,我們傳統上接受 ZFC 作為「集合論」的本體,但 topos theory 的發展給出另一套定義 ETCS https://en.wikipedia.org/wiki/Elementary_Theory_of_the_Category_of_Sets!ETCS 說我們覺得集合論是「由 sets 與 functions 構成的 well-pointed topos,有自然數 object 與 Epics split」。
這個定義並沒有循環定義(但使用了短語簡化說法),因為 sets 跟 functions 的公理可以直接給出,ETCS 並沒有比 ZFC 不穩固。
事實上我們甚至知道 ETCS 跟 ZFC 的差異,ETCS + replacement(https://en.wikipedia.org/wiki/Axiom_schema_of_replacement)等價於 ZFC 的推理能力。ZFC 中的某部份等價於 ETCS(參考 Sheaves in Geometry and Logic: A First Introduction to Topos Theory VI. 10)
重點是,既然沒辦法保證討論主題的永久不變,那就應該紀錄當下對主題的洞見,因而在未來仍可從思想中復原出結構。
Definition. Pfaffian [math-000P]
Definition. Pfaffian [math-000P]
Let be a skew-symmetric endomorphism of a vector space (hence can also be view as a tensor: ) and is even, the Pfaffian of is the number defined as the constant factor in the tensor equality:
where is an orthonormal basis of .
The sign of Pfaffian depends on the orientation of the orthonormal basis.
An Agda Framework for Synthetic Mathematics [math-000K]
An Agda Framework for Synthetic Mathematics [math-000K]
https://samtoth.github.io/agda-synthetic-categories/index/index.xml
Theorem. Borsuk–Ulam [math-000L]
Theorem. Borsuk–Ulam [math-000L]
If is continuous then there exists a point such that .
Lemma. [math-000M]
Lemma. [math-000M]
If is continuous and antipode-preserving, then there exists a point such that .
Proof
Use standard stereographic projection, we can see and charts gives exactly the same coordinate system at equator (i.e. where its embedding coordinate with ). This also tells the equator is a in because .
By continuous and antipode-preserving, preserves such an equator (we denote ) to (with any deformation that still an antipode shape) and must bound a set contains .
By continuous, both of two open sets of , complement of , needs to be mapped to cover the subset of which bounded by , so there exists a point such that .
Proof
Define , is continuous.
By
is antipode-preserving.
By the lemma, there is a point such that , so then .
Determinant of Skew-Symmetric Matrices [math-000V]
Determinant of Skew-Symmetric Matrices [math-000V]
This problem arose from studying the book Lectures on the Geometry of Manifolds: Suppose is a real vector space, and is a symplectic duality, then has even dimension.
I can make some concrete computation on dimension 2 and 3 and roughly understand the reason, but I have no general proof.
After a month, I found a solution:
Proof. Using the properties of matrix column operations [math-000W]
Proof. Using the properties of matrix column operations [math-000W]
Since the multiplication factor of a matrix column can be extracted as a basis, flip the column 1 (i.e. the whole column multiply ) we have
Following this pattern, flipping column 2 gives us:
Let be an skew-symmetric matrix. After flipping all columns, we obtain , therefore
By definition, skew-symmetric means , so
When is odd, this gives us
Therefore must be 0.
After formalize this statement https://github.com/dannypsnl/blackboard/commit/2c0de90a98c24ae57bd30bc47ed8c3b6a75f2664, I found this need the field is charateristic 0, sure indeed satisfies that, this point to me is that Lean can help me refine my ideas.
If represents a duality, then . Therefore cannot be odd—it must be even.
What I Wish I Knew When Learning HoTT [tt-000P]
What I Wish I Knew When Learning HoTT [tt-000P]
Dependent Pattern Matching [ag-0001]
Dependent Pattern Matching [ag-0001]
{-# OPTIONS --safe --without-K #-} module ag-0001 where open import MLTT.Spartan
依賴類型有一些不同於常見語言的特徵,像是下面定義的這個類型
data So : 𝟚 → 𝓤₀ ̇ where oh : So ₁ ho : So ₀
在模式比對時 constructor oh 跟 ho
提供了變數 b 的訊息。
xxx : {b : 𝟚} → So b → 𝟚 xxx {b} oh = b -- 這裡 b 一定是 ₁ xxx {b} ho = b -- 這裡 b 一定是 ₀
Lecture. Domain Theory [dt-0000]
Lecture. Domain Theory [dt-0000]
Course. CS208 Logic & Algorithms [MSP-cs208]
Course. CS208 Logic & Algorithms [MSP-cs208]
Code and Materials for an interactive online course on Logic (part of Strathclyde's CS208 Logic and Algorithms module)
- project link: https://github.com/msp-strath/cs208-logic
- site link: https://personal.cis.strath.ac.uk/robert.atkey/cs208/index.html
Tool. agda 的開發工具 [agda-0001]
Tool. agda 的開發工具 [agda-0001]
我使用的編輯器工具是 Agda Mode on VS Code,也可以用 emacs 之類的。常用操作有
ctrl+c, ctrl+l 會編譯檢查檔案,假設程式中有
?,會被替換成所謂的 hole{! !},其實就是待寫的程式ctrl+c, ctrl+, 可以窺看 hole 的目標類型,與當前 context 有哪些 term 可用
ctrl+c, ctrl+r 會把 hole 中你打的程式碼往前提取,當然前提是類型是正確的
ctrl+c, ctrl+m 會把 hole 中你打的程式碼直接當成結果,一樣類型要是正確的
一般來說一個 agda 定義如下
hello : A → B hello a = {! !}ctrl+c, ctrl+c 會問你要把哪個變數用構造子分開,回答
a,假設有a1與a2兩個構造子,程式就會變成hello : A → B hello a1 = {! !} hello a2 = {! !}
使用 Linux 的使用者可以更改預設的 copy/cut 指令以免衝突。
已完成的軟體 [software-0007]
已完成的軟體 [software-0007]
已完成的軟體這種概念,是指一個軟體的功能已經沒有大幅度更動的必要,可以長期使用在產品上,而軟體本身只會進行必要的安全與移植性更新。我在 https://josem.co/the-beauty-of-finished-software/ 讀到這個想法。對應到筆記軟體上,我不希望軟體一直更新,尤其是當我一打開工具需要寫筆記時,上面的更新按鈕非常的讓人煩躁。同時,這個想法也是一種解放我們原先對軟體想像的開端,比起軟體如何如何,更重要的是真的去做,外部連結裡面也談到冰與火之歌正是用這樣的軟體寫出。
git send-email setup with Protonmail [software-0006]
git send-email setup with Protonmail [software-0006]
In the original setup I already explain the configuration, to do the same with Protonmail will need to install Proton Mail Bridge(https://proton.me/mail/bridge), then with configuration as below.
[sendemail] smtpEncryption = STARTTLS smtpServer = 127.0.0.1 smtpUser = <your id>@protonmail.com smtpServerPort = 1025 smtpPass = <your password>
Definition. point-surjective [math-000A]
Definition. point-surjective [math-000A]
A morphism is point-surjective iff for every point , there exists a point that lifts (satisfy ).
git send-email 的設定 [software-0004]
git send-email 的設定 [software-0004]
I use gmail, and hence, I need to get a Google app password. After having the password, one has to setup ~/.gitconfig with content:
[sendemail] smtpEncryption = tls smtpServer = smtp.gmail.com smtpUser = <your id>@gmail.com smtpServerPort = 587 smtpPass = <your password>
Then you are able to use git send-email command:
git switch -c branch-patch git format-patch main git send-email 0001-***********.patch
prompt will ask some questions, an important one is which mailing list is your target? After command success, your patch are sent.
For certain git repository you're working on, can config local repository via git config --edit, and add below to omit email list in command line.
[sendemail] to = <target email list>
Mastodon 私訊相比於一般通訊軟體 e.g. LINE, Telegram [software-0003]
Mastodon 私訊相比於一般通訊軟體 e.g. LINE, Telegram [software-0003]
好處
- 可以有效分類特定話題,例如一個串是講約去哪裡吃飯、另一個串講專業內容
- 可以用僅限提及的人,限制可見性,所以可以形成一定程度的群組概念
壞處
- 兩方站點的站長都能看到內容
- 客戶端不支援把一群提及名單固定成群組,這或許是一個可行的客戶端新功能
壞處的可能解法:公佈自己的 public key 讓對方加密訊息再傳,配上專用客戶軟體或許可以做的更方便
let Racket GC manage your FFI object [software-0005]
let Racket GC manage your FFI object [software-0005]
All you need are deallocator and allocator from ffi/unsafe/alloc.
(require ffi/unsafe
ffi/unsafe/define
ffi/unsafe/alloc)
(define-ffi-definer define-xxx
(ffi-lib "" '(#f)))
(define-xxx free-yyy (_fun _YyyRef -> _void)
#:c-id yyy_delete
#:wrap (deallocator))
(define-xxx make-yyy (_fun -> _YyyRef)
#:c-id yyy_new
#:wrap (allocator free-yyy)) Tool. ngrok [software-0002]
Tool. ngrok [software-0002]
Sometimes we didn't have public ip, but temporary wants to test website, ngrok can help in this situation.
# expose localhost:8080 by HTTP $ ngrok http 8080 # expose localhost:8080 by TCP $ ngrok tcp 8080
XDP [software-0001]
XDP [software-0001]
XDP is eXpress Data Path, it's a technology about putting a BPF code virtual machine on the NIC(network interface controller) driver before kernel network stack so that we can filter the packet before kernel, it would make processing speed greater.
We can do following things on the packet:
XDP_PASS: allow the packet to pass throughXDP_DROP: drop the packetXDP_TX: bounce the packet back on the same interfaceXDP_REDIRECT: redirects the packet to another interface
Here is an example of counting how many IPv4/6 packets be dropped.
package main
import (
"fmt"
"os"
"os/signal"
bpf "github.com/iovisor/gobpf/bcc"
)
// bcc is from iovisor/bcc this project
/*
#cgo CFLAGS: -I/usr/include/bcc/compat
#cgo LDFLAGS: -lbcc
#include
#include
void perf_reader_free(void *ptr);
*/
import "C"
const source string = `
#define KBUILD_MODNAME "foo"
#include
#include
#include
#include
#include
#include
#include
BPF_TABLE("array", int, long, dropcnt, 256);
static inline int parse_ipv4(void *data, u64 nh_off, void *data_end) {
struct iphdr *iph = data + nh_off;
if ((void*)&iph[1] > data_end)
return 0;
return iph->protocol;
}
static inline int parse_ipv6(void *data, u64 nh_off, void *data_end) {
struct ipv6hdr *ip6h = data + nh_off;
if ((void*)&ip6h[1] > data_end)
return 0;
return ip6h->nexthdr;
}
int xdp_prog1(struct xdp_md *ctx) {
void* data_end = (void*)(long)ctx->data_end;
void* data = (void*)(long)ctx->data;
struct ethhdr *eth = data;
uint64_t nh_off = sizeof(*eth);
if (data + nh_off > data_end)
return XDP_DROP;
uint16_t h_proto = eth->h_proto;
if (h_proto == htons(ETH_P_8021Q) || h_proto == htons(ETH_P_8021AD)) {
struct vlan_hdr *vhdr;
vhdr = data + nh_off;
nh_off += sizeof(struct vlan_hdr);
if (data + nh_off > data_end)
return XDP_DROP;
h_proto = vhdr->h_vlan_encapsulated_proto;
}
if (h_proto == htons(ETH_P_8021Q) || h_proto == htons(ETH_P_8021AD)) {
struct vlan_hdr *vhdr;
vhdr = data + nh_off;
nh_off += sizeof(struct vlan_hdr);
if (data + nh_off > data_end)
return XDP_DROP;
h_proto = vhdr->h_vlan_encapsulated_proto;
}
int index;
if (h_proto == htons(ETH_P_IP))
index = parse_ipv4(data, nh_off, data_end);
else if (h_proto == htons(ETH_P_IPV6))
index = parse_ipv6(data, nh_off, data_end);
else
index = 0;
long *value;
value = dropcnt.lookup(&index);
if (value) lock_xadd(value, 1);
return XDP_DROP;
}
`
func usage() {
fmt.Printf("Usage: %v \n", os.Args[0])
fmt.Printf("e.g.: %v eth0\n", os.Args[0])
os.Exit(1)
}
func main() {
if len(os.Args) != 2 {
usage()
}
module := bpf.NewModule(source, []string{
"-w",
})
defer module.Close()
fn, err := module.Load("xdp_prog1", C.BPF_PROG_TYPE_XDP, 1, 65536)
if err != nil {
fmt.Fprintf(os.Stderr, "Failed to load xdp prog: %v\n", err)
os.Exit(1)
}
device := os.Args[1]
if err := module.AttachXDP(device, fn); err != nil {
fmt.Fprintf(os.Stderr, "Failed to attach xdp prog: %v\n", err)
os.Exit(1)
}
defer func() {
if err := module.RemoveXDP(device); err != nil {
fmt.Fprintf(os.Stderr, "Failed to remove XDP from %s: %v\n", device, err)
}
}()
fmt.Println("Dropping packets, hit CTRL+C to stop")
sig := make(chan os.Signal, 1)
signal.Notify(sig, os.Interrupt, os.Kill)
dropcnt := bpf.NewTable(module.TableId("dropcnt"), module)
<-sig
fmt.Println("\n{IP protocol-number}: {total dropped pkts}")
for it := dropcnt.Iter(); it.Next(); {
key := bpf.GetHostByteOrder().Uint32(it.Key())
value := bpf.GetHostByteOrder().Uint64(it.Leaf())
if value > 0 {
fmt.Printf("%v: %v pkts\n", key, value)
}
}
} Algorithm. Mark sweep GC [cs-0008]
Algorithm. Mark sweep GC [cs-0008]
Mark-Sweep is a classic GC algorithm, it's combined with two parts, mark and sweep.
mark(root):
if not marked?(root):
mark(root)
for obj in knowns(root):
mark(obj)
sweep(heap):
for obj in heap:
if marked?(obj):
unmark(obj)
else:
release(obj)
If we run collection (mark-sweep), then since each object is reachable from root, so no one would be released.
After do some executions, obj1 don't need obj3 anymore, so it became:
Now when we run collection, obj3 is unreachable from root, so it won't be marked! When running to sweep, it will be dropped.
Projects [projs]
Projects [projs]
Contribution. racket-langserver [racket-langserver]
Contribution. racket-langserver [racket-langserver]
A Language Server Protocol implementation for Racket.
- implement cross-file jump to definition. #59
- auto formatting: remove trailing whitespace. #61
- implement inlay hints. #84
- add diagnostic and code action for unused variables. #87
- support notification
workspace/didChangeWorkspaceFolders. #140 - support notification
workspace/didRenameFiles. #144 - support installed Racket languages (e.g. Rhombus). #150
- support notification
workspace/didChangeWatchedFiles. #151 - support configuration request
workspace/configuration. #156 - fix server configuration updation #164
- Extract server concept to remove complicated IO interaction #173
- Respect client capabilities #182
- Record
rootUriandrootPathin initialize params as workspace folders #184 - Find workspace references (limits to opened files) #160
- reduce costs of service workspace-references #195
tr [tr-0000]
tr [tr-0000]
A site generator based on a collection of racket/scribble programs.
下面著手描述這個專案的核心想法
地址唯一性 [tr-0003]
地址唯一性 [tr-0003]
每張卡片應有唯一的地址
生成 embed 與 index HTML [tr-0001]
生成 embed 與 index HTML [tr-0001]
embed 之間需要按引用關係構造,所以用 topological sort 排序(從 metadata.json 中復原依賴關係)後按順序編譯
通過分成兩階段生成,可以讓 index 引入 embed 的內容
raco tr next 與使用方式 [tr-0002]
raco tr next 與使用方式 [tr-0002]
讓 raco tr next xxx 生成新的地址,就可以用 code $(raco tr next xxx).scrbl 這樣的方式開啟新檔案
數學支援 [tr-0004]
數學支援 [tr-0004]
用 Katex 支援公式,用 LaTeX 支援複雜的圖
LaTeX 工作的獨立標籤 [tr-0006]
LaTeX 工作的獨立標籤 [tr-0006]
每個 address yyy 對 LaTeX 會創造新的相關的 _tmp/yyy/tex3212.tex 之類的檔案,tex3212 是用 gensym 產生。
如此一來 *.tex 檔案可知道自己是哪個 address 產出,如果 source 沒有更新便不編譯。
RSS 與 searching [tr-0005]
RSS 與 searching [tr-0005]
利用預先生成的 addr.metadata.json 進一步生成 RSS 與索引資料
tr/card [tr-0008]
tr/card [tr-0008]
Code changes: https://github.com/dannypsnl/tr/commit/c1000033203c4216cdccff53bac7f2288a76b867
在 metadata 裡面加入 locals 這個概念,在這個陣列裡面儲存 title 跟 taxon 資訊。遞迴時先標好地址,把資訊存到相應的地址中,就得到平坦的結構。於是就不一定需要開新的檔案來寫新的 card 了。
config 中可以設定 fediverse 的帳號 [tr-0009]
config 中可以設定 fediverse 的帳號 [tr-0009]
在 site.json 中安插 entry
"fedi": {
"site": "a fediverse site",
"handle": "your account id on it"
} sauron [sauron]
sauron [sauron]
A DrRacket plugin to make it experience like an IDE
Contribution. agda [agda]
Contribution. agda [agda]
Contribution. magic-racket [magic-racket]
Contribution. magic-racket [magic-racket]
The best coding experience for Racket in VS Code.
- Open selection in macro stepper. #148
Contribution. agda-mode-vscode [agda-mode-vscode]
Contribution. agda-mode-vscode [agda-mode-vscode]
agda-mode on VSCode
- Provide hover text to hint about how to type a symbol. #258
bib2tr [bib2tr]
bib2tr [bib2tr]
A tool to convert .bib file to a list of reference cards.
html2scrbl [html2scrbl]
html2scrbl [html2scrbl]
A web tool to convert input HTML to scribble/html
violet [violet]
violet [violet]
violet is a programming language I created for researching dependent type in use. If you want to contribute the project, you will need the below information:
racket-llvm [racket-llvm]
racket-llvm [racket-llvm]
LLVM bindings for racket
typed/racket eff [typed-racket-eff]
typed/racket eff [typed-racket-eff]
An effect system integrated with typed/racket.
agda-tree [agda-tree]
agda-tree [agda-tree]
Converts agda produced *.tree to valid *.tree.
html2tree [html2tree]
html2tree [html2tree]
Converts html syntax to forester namespace html syntax.
Algebraic Graph [algebraicgraph]
Algebraic Graph [algebraicgraph]
Formalize Algebraic graphs with class in Lean.
Contribution. llir/llvm [llir]
Contribution. llir/llvm [llir]
redux [redux]
redux [redux]
type CountingModel struct {
rematch.Reducer
State int
Increase *rematch.Action `action:"IncreaseImpl"`
}
func (c *CountingModel) IncreaseImpl(s, payload int) int {
return s + payload
}
func main() {
c := &CountingModel {
State: 0,
}
store := store.New(c)
store.Dispatch(c.Increase.With(30))
store.Dispatch(c.Increase.With(20))
fmt.Printf("result: %d\n", store.StateOf(c)) // expect: 50
} rocket [rocket]
rocket [rocket]
import (
"github.com/dannypsnl/rocket"
)
type User struct {
Name string `route:"name"`
Age uint64 `route:"age"`
}
func hello(u *User) string {
return "Hello " + u.Name + ", your age is " + strconv.FormatUint(u.Age, 10)
}
// main.go
func main() {
rocket.Ignite(8080).
Mount(
// put `hello` under a path `/user/:name/:age`, where `:name` and `:age` are variant parameters
rocket.Get("/user/:name/:age", hello),
).
Launch()
} Talks [talks]
Talks [talks]
Reference. General Recursion [general-recursion]
Reference. General Recursion [general-recursion]
Slide: /hami2023
Kaohsiung Medical University, Healthcare Adminstration and Medical Informatics
Reference. types cross languages [type-cross-language]
Reference. types cross languages [type-cross-language]
Slide: https://dannypsnl.github.io/typecafe2023/typecafe2023.html
∞-type café 2023
Reference. Can this program stop? [program-termination]
Reference. Can this program stop? [program-termination]
Slide: https://dannypsnl.github.io/hami2022/hami2022.html
Kaohsiung Medical University, Healthcare Adminstration and Medical Informatics
Reference. closure conversion [closure-conversion]
Reference. closure conversion [closure-conversion]
Slide: https://dannypsnl.me/~slide/2022-07-closure-conversion.pdf
coscup 2022
Reference. clojure isn't lisp enough [clojure-isnt-lisp-enough]
Reference. clojure isn't lisp enough [clojure-isnt-lisp-enough]
Slide: https://dannypsnl.me/~slide/2021-04-clojure-isnt-lisp-enough.pdf
clojure taiwan
Reference. macro as type [macro-as-type]
Reference. macro as type [macro-as-type]
- slides: https://dannypsnl.me/~slide/2021-03-racketfest.rkt
- video: https://youtu.be/BLHxUzj7F-Q
- venue: racketfest 2021