Model mapping TT to untyped LC [ag-000Y]
Model mapping TT to untyped LC [ag-000Y]
{-# OPTIONS --without-K #-} open import MLTT.Spartan hiding (Π; zero; succ) open import UF.FunExt open import ag-000V open import ag-000W module ag-000Y (fe : Fun-Ext) where
A model mapping TT to untyped lambda calculus.
module LC-TT {𝓤 𝓥 : Universe} (l : LC {𝓥}) where open LC open TT open TT-sorts open TT-ctors ex-sorts : TT-sorts {𝓤} {𝓥} ex-sorts .Ty = 𝟙 ex-sorts .Tm _ = l .Λ ex-ctors : TT-ctors ex-sorts ex-ctors .Π A B = ⋆ ex-ctors .lam f = l .lambda f ex-ctors .app f x = l .apply f x ex-ctors .lam-app = l .η _ ex-ctors .app-lam {a}{b}{f} = (λ x → l .apply (l .lambda f) x) =⟨ dfunext fe (λ x → l .β f x) ⟩ (λ x → f x) =⟨ refl ⟩ f ∎ ex-ctors .U = ⋆ ex-ctors .El _ = ⋆ ex-ctors .Nat = ⋆ ex-ctors .zero = zeroΛ l ex-ctors .succ x = succΛ l x ex-ctors .elim-Nat X ze su n = recΛ l ze su n ex-ctors .elim-Nat-zero = recΛβ-zero l ex-ctors .elim-Nat-succ = recΛβ-succ l ex : TT {𝓤} {𝓥} ex .sorts = ex-sorts ex .ctors = ex-ctors
SOGAT of type theory with -types, a Tarski universe, and natural numbers [ag-000W]
SOGAT of type theory with -types, a Tarski universe, and natural numbers [ag-000W]
Learn from https://github.com/kontheocharis/erasure-agda
{-# OPTIONS --without-K --confluence-check #-} module ag-000W where open import MLTT.Spartan hiding (Π; zero; succ) coe : {X X' : 𝓤 ̇ } → X = X' → X → X' coe = transport id
TT 要用的 sorts,以及如果 Type 相等,可以轉換 term 用的 helper
coeTm
record TT-sorts : (𝓤 ⊔ 𝓥)⁺ ̇ where field Ty : 𝓤 ̇ Tm : Ty → 𝓥 ̇ coeTm : ∀ {A B : Ty} → A = B → Tm A → Tm B coeTm p a = coe (ap Tm p) a
TT 的 SOGAT
module _ (sorts : TT-sorts {𝓤} {𝓥}) where open TT-sorts sorts private variable A B C : Ty X Y Z : Tm _ → Ty t u v : Tm _ f g h : (a : Tm _) → Tm _ eq : _ = _ record TT-ctors : (𝓤 ⊔ 𝓥)⁺ ̇ where field -- Pi types Π : (A : Ty) → (Tm A → Ty) → Ty lam : ((a : Tm A) → Tm (X a)) → Tm (Π A X) app : Tm (Π A X) → (a : Tm A) → Tm (X a) lam-app : lam (app t) = t app-lam : app (lam f) = f -- Universe U : Ty El : Tm U → Ty -- Natural numbers Nat : Ty zero : Tm Nat succ : Tm Nat → Tm Nat elim-Nat : (X : Tm Nat → Ty) → (Tm (X zero)) → ((n : Tm Nat) → Tm (X n) → Tm (X (succ n))) → (n : Tm Nat) → Tm (X n) -- Computation for elim-Nat elim-Nat-zero : ∀ {mz ms} → elim-Nat X mz ms zero = mz elim-Nat-succ : ∀ {mz ms n} → elim-Nat X mz ms (succ n) = ms n (elim-Nat X mz ms n) record TT : (𝓤 ⊔ 𝓥)⁺ ̇ where field sorts : TT-sorts {𝓤} {𝓥} open TT-sorts sorts public field ctors : TT-ctors sorts open TT-ctors ctors public
Definition. Riemann curvature tensor [B2D1]
Definition. Riemann curvature tensor [B2D1]
The curvature of a Riemannian manifold is a tensor
where are vector fields, is the Levi-Civita connection of the metric (see Lectures on the Geometry of Manifolds Proposition 4.1.9.).
In local coordinates we have
In terms of the Christoffel symbols we have
Lowering the indices we have a new tensor
Theorem. The Hairy Ball Theorem [DRE0]
Theorem. The Hairy Ball Theorem [DRE0]
用 constant vector field on plane 然後拉回 的定義方法很妙。
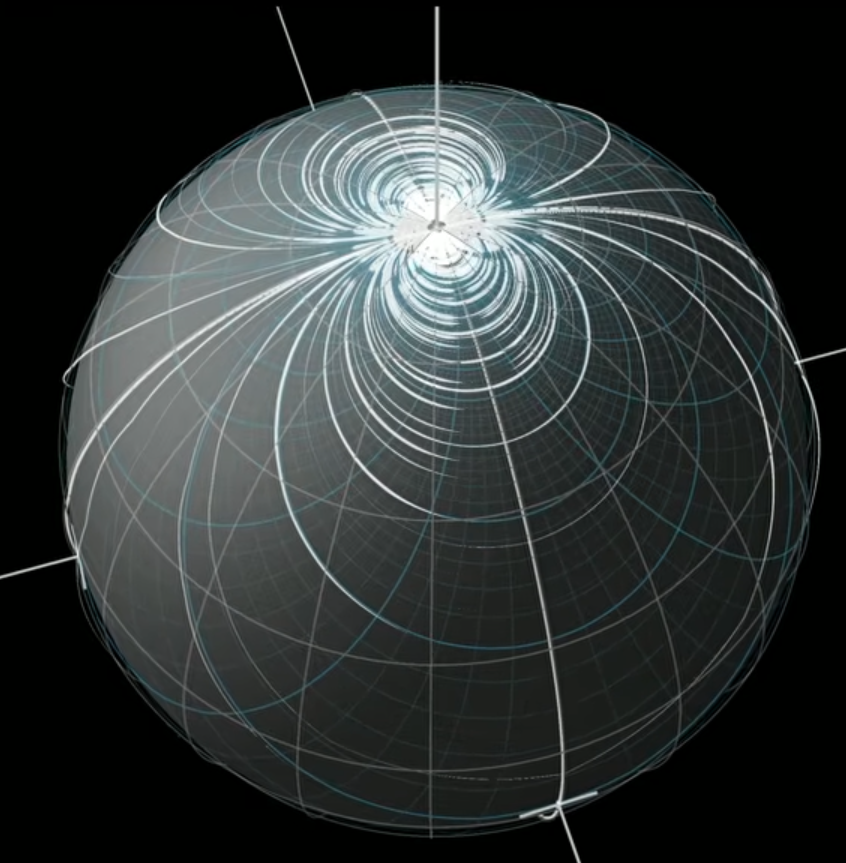
定理的證明是用 Flux 不變,但如果有處處非零的連續向量場,就可以讓 Flux 改變,矛盾。因此這樣的向量場不可能存在。
3-sphere (群 ) 跟 [JRT2]
3-sphere (群 ) 跟 [JRT2]
用 quotient 掉 antipodal points 會得到 Real projective space 。
Proposition. is not simple [local-1]
Proposition. is not simple [local-1]
Proof. [local-0]
Proof. [local-0]
因為 是 的 normal subgroup: 跟 for all 都還是屬於 。
而 nontrivial,有 nontrivial normal subgroup 的群 not simple
是群 :The group of rotations of 。 is simple 所以跟 不是同一個群
作為一個群可以視為 2x2 複數矩陣的群,元素為
這又稱為 The special unitary group 。
Definition. Hopf bundle [5A3M]
Definition. Hopf bundle [5A3M]
Identify the unit odd dimensional sphere with the submanifold
an -action on given by
The complex projective space is isomorphic to , the group corresponds to . This quotient map is a principal bundle called Hopf bundle.
- by definition of
- Use (because , these describe all points in the projective space). The map defined by then
SOGAT of untyped lambda calculus [ag-000V]
SOGAT of untyped lambda calculus [ag-000V]
{-# OPTIONS --safe --without-K #-} open import MLTT.Spartan hiding (id) open import ag-0005 module ag-000V where
SOGAT of untyped lambda calculus.
record LC : 𝓤 ⁺ ̇ where field Λ : 𝓤 ̇ lambda : (f : Λ → Λ) → Λ apply : Λ → Λ → Λ β : ∀ f x → apply (lambda f) x = f x η : ∀ f → lambda (λ x → apply f x) = f _$_ : Λ → Λ → Λ x $ y = apply x y infixl 30 _$_ syntax lambda (λ x → t) = ƛ x ⇒ t zeroΛ : Λ zeroΛ = ƛ z ⇒ ƛ s ⇒ z succΛ : Λ → Λ succΛ n = ƛ z ⇒ ƛ s ⇒ (s $ n $ (n $ z $ s)) id : Λ id = ƛ x ⇒ x recΛ : Λ → (Λ → Λ → Λ) → Λ → Λ recΛ zr su n = n $ zr $ (ƛ k ⇒ ƛ sk ⇒ su k sk) recΛβ-zero : ∀ {zr su} → recΛ zr su zeroΛ = zr recΛβ-zero {zr} {su} = (ap (_$ (ƛ k ⇒ ƛ sk ⇒ su k sk)) (β (λ z → ƛ s ⇒ z) zr)) ∙ (β (λ _ → zr) (ƛ k ⇒ ƛ sk ⇒ su k sk)) recΛβ-succ : ∀ {zr su n} → recΛ zr su (succΛ n) = su n (recΛ zr su n) recΛβ-succ {zr} {su} {n} = (ap (_$ (ƛ k ⇒ ƛ sk ⇒ su k sk)) (β (λ z → ƛ s ⇒ (s $ n $ (n $ z $ s))) zr)) ∙ (β (λ s → s $ n $ (n $ zr $ s)) (ƛ k ⇒ ƛ sk ⇒ su k sk)) ∙ (ap (_$ (n $ zr $ (ƛ k ⇒ ƛ sk ⇒ su k sk))) (β (λ k → ƛ sk ⇒ su k sk) n)) ∙ (β (λ sk → su n sk) (n $ zr $ (ƛ k ⇒ ƛ sk ⇒ su k sk))) embed-nat : ℕ → Λ embed-nat 0 = zeroΛ embed-nat (succ x) = succΛ (embed-nat x)
Lambda calculus (Second-order algebraic theories) universe polymorphic extended.
代數幾何:視 -element 為函數 [WYCP]
代數幾何:視 -element 為函數 [WYCP]
在 manifold 上我們可以定義 。在代數幾何裡面我們想要抽象並仿造這個結構,所以若 為一點(亦同時是 prime ideal),residue field at point 定義為 the field of fractions of the quotient ring
那麼,每個 取 使 可以被視為一個「函數」,不過在不同點 的 codomain 都不同。構造即取 再取 。
Status of the smooth rectangular Peg problem [VEYQ]
Status of the smooth rectangular Peg problem [VEYQ]
https://www.math.columbia.edu/~ums/Peg%20problem%20-%20slides.pdf
- Emch (1913) solved the problem for smooth convex curves. (Proof uses configuration spaces and homology.)
- Schnirelman (1929) solved it for any smooth Jordan curve.
Theorem. Vaughan (1977) [local-0]
Theorem. Vaughan (1977) [local-0]
Every continuous Jordan curve contains four points forming the vertices of some rectangle. This is what 3b1b did, see video here.
Theorem. Greene-Lobb (2020) [local-1]
Theorem. Greene-Lobb (2020) [local-1]
Given a smooth Jordan curve and a rectangle in the plane, then contain four points forming the vertices of a rectangle similar to R.
Theorem. Barr's theorem [KGRZ]
Theorem. Barr's theorem [KGRZ]
If is a Grothendieck topos, then there is a surjective geometric morphism
where satisfies the axiom of choice.
presheaves exponential 同構的推導 [21ME]
presheaves exponential 同構的推導 [21ME]
Topos Theory 的 1.12
令 為 category 的 presheaves,那麼
Proof. [local-0]
Proof. [local-0]
- 用 Presheaves are colimits of representables 改寫
- Contravariant 用到的是 Hom-functor preserves limits
Proposition. Hom-functor preserves limits [math-TGEI]
Proposition. Hom-functor preserves limits [math-TGEI]
This is a very useful property of hom-functor.
Let be a category, then its hom-functor can be wrote as
If the limit exists in , then for all there is a natural isomorphism
If the colimit exists in , then for all there is a natural isomorphism
See nLab for more details.
Definition. Holonomy [math-L2W1]
Definition. Holonomy [math-L2W1]
Let be a vector bundle with a connection . The holonomy of along a closed path is the parallel transport along .
Definition. Parallel transport [math-XU4I]
Definition. Parallel transport [math-XU4I]
Let be a vector bundle with a connection . For any smooth path we will define a linear isomorphism called the parallel transport along .
The construction [local-0]
The construction [local-0]
More precisely, we construct a family of linear isomorphisms:
for all . Consider arbitrary , let be a vector, then define , we know . What we are searching is a "constant" path, in the sense that derivative is , hence we want
so this suggests a way of defining : For any and any , define as the value at of the solution of the initial value problem:
And this is a system of linear ordinary differential equations in disguise.
Definition. Covariant Derivative (Linear Connection) [math-HCIJ]
Definition. Covariant Derivative (Linear Connection) [math-HCIJ]
Let be a vector bundle. A covariant derivative on is a -linear map
such that, for all and all , we have
where denotes the space of smooth sections of over .
Remind that
Therefore, has a more traditional view
Note when a map is an equivalence [RNNM]
Note when a map is an equivalence [RNNM]
For a given function , the following are two correct definitions of f is an equivalence.
Defintion. Voevodsky's [ag-000T]
Defintion. Voevodsky's [ag-000T]
is an equivalence if its fibers are contractible (or singletons): For every , the type
fiber : {X : 𝓤 ̇ } {Y : 𝓥 ̇ } → (X → Y) → Y → 𝓤 ⊔ 𝓥 ̇ fiber f y = Σ x ꞉ domain f , f x = y
has the property that there is a distinguished element σ0 : fiber f y such that σ = σ0 for all σ : fiber f y.
is-equiv : {X : 𝓤 ̇ } {Y : 𝓥 ̇ } → (f : X → Y) → 𝓤 ⊔ 𝓥 ̇ is-equiv f = ∀ (y : codomain f) → Σ σ₀ ꞉ fiber f y , ∀ (σ : fiber f y) → σ = σ₀
Defintion. Joyal's [ag-000U]
Defintion. Joyal's [ag-000U]
is an equivalence if it has a section and also has a retraction:
{-# OPTIONS --safe --without-K #-} module ag-000U where open import MLTT.Spartan open import UF.Base open import UF.Sets open import UF.Sets-Properties
is-equiv : {X : 𝓤 ̇ } {Y : 𝓥 ̇ } → (f : X → Y) → 𝓤 ⊔ 𝓥 ̇ is-equiv f = (Σ s ꞉ (codomain f → domain f) , f ∘ s ∼ id) × (Σ r ꞉ (codomain f → domain f) , r ∘ f ∼ id)
Of course, the second post in thread is more important, there is a wrong definition, and Escardo shows why it's wrong.
什麼是量子幾何 [FWA9]
什麼是量子幾何 [FWA9]
Why , A Four Dimensional Proof [E963]
Why , A Four Dimensional Proof [E963]
JIT: Write XOR Execute policy [UIC7]
JIT: Write XOR Execute policy [UIC7]
所謂的 W^X (Write XOR Execute) policy 是指不要讓記憶體同時是 PROT_WRITE 跟 PROT_EXEC,所以正確的配置方式是(參見 mmap)
- 先設定成
PROT_READ | PROT_WRITE - 等寫完指令再改成
PROT_READ | PROT_EXEC(像是用mprotecthttps://man7.org/linux/man-pages/man2/mprotect.2.html)
然後才能真的執行這段程式。
Corollary. About Boolean ring [math-HS0H]
Corollary. About Boolean ring [math-HS0H]
Let be a Boolean ring (see nLab) and .
Tool. Unsure Calculator [VIPY]
Tool. Unsure Calculator [VIPY]
Theorem. The field of fractions is a torsion-free module [math-3E35]
Theorem. The field of fractions is a torsion-free module [math-3E35]
Let be an integral domain, and is the field of fractions of . Then is a torsion-free -module (see The Stacks project tag/0549).
Proof. [local-0]
Proof. [local-0]
We want to show that the only torsion element of is . Every element of has the form where , now suppose is a torsion. Then there exists a such that
which leads
in an integral domain, this leads or , but by definition, hence . Which means is , be torsion is be zero in , is a torsion-free -module.
Theorem. Premanifold 為 Hausdorff 的等價條件 [math-T4B3]
Theorem. Premanifold 為 Hausdorff 的等價條件 [math-T4B3]
令 為一個 premanifold(field 為 或是 )。則以下條件等價:
- 為 Hausdorff 空間
- 對於 中任意相異兩點 (),存在開集 使得 ,且在 中,存在函數 使得
Proof. [local-0]
Proof. [local-0]
(2) ⇒ (1):設 為相異兩點。由條件 (2),存在開集 使得 ,且存在 使得 。
令 。因為 為 smooth 函數,存在 的開鄰域 使所有 ,有 。
同理,存在 的開鄰域 使得對所有 ,有 。於是我們知道 ,因為如果存在 ,則:
為矛盾,也就是說不存在這種 。因此 為 Hausdorff 空間。
(1) ⇒ (2):設 為相異兩點。因為 為 Hausdorff 空間,存在不相交的開鄰域 和 使得 。
因為 為 premanifold,存在 open cover 使得每個 與某個 local ringed space 同構。因此存在 和 使得 且 。
考慮開集 和 。因為 ,我們有 。
取 的開鄰域 及函數 使得 (此函數對應於 stalk 的 maximal ideal 中的元素)。同理,取 的開鄰域 及函數 使得 (對應於 stalk 中不在 maximal ideal 的元素)。
令 ,則 為開集且 。因 與 不相交,可定義函數 ,在 上取 ,在 上取 。於是 而 , 與 滿足條件 (2)。
NOTE: Explicit Weakening [ag-000S]
NOTE: Explicit Weakening [ag-000S]
在 Substitution Without Copy and Paste 結尾也有提過這篇,就來稍微看一下。
Explicit Weakening
{-# OPTIONS --rewriting --no-level-universe #-} module ag-000S where open import MLTT.Spartan hiding (Type; id) {-# BUILTIN REWRITE _=_ #-} cong₂ : ∀ {A B C : 𝓤 ̇ } (f : A → B → C) {x y u v} → x = y → u = v → f x u = f y v cong₂ f refl refl = refl
data Type : 𝓤₀ ̇ where base : Type _⇒_ : Type → Type → Type infixr 7 _⇒_ variable A B C : Type data Con : 𝓤₀ ̇ where ∅ : Con _▷_ : Con → Type → Con infixl 5 _▷_ variable Γ Δ Θ Ξ : Con data _⊢_ : Con → Type → 𝓤₀ ̇ where • : Γ ▷ A ⊢ A _↑ : (M : Γ ⊢ B) ------------ → Γ ▷ A ⊢ B ƛ_ : (N : Γ ▷ A ⊢ B) → Γ ⊢ A ⇒ B _·_ : (L : Γ ⊢ A ⇒ B) (M : Γ ⊢ A) ----------------------------- → Γ ⊢ B infix 5 ƛ_ infix 4 _⊢_ infixl 7 _·_ variable L M N P Q : Γ ⊢ A data _⊨_ : Con → Con → 𝓤₀ ̇ where id : Δ ⊨ Δ _↑ : (σ : Γ ⊨ Δ) → Γ ▷ A ⊨ Δ _▷_ : (σ : Γ ⊨ Δ) (M : Γ ⊢ A) ------------ → Γ ⊨ Δ ▷ A infix 4 _⊨_ infix 8 _↑ variable σ τ υ : Γ ⊨ Δ pattern △ = _ ▷ _
Instantiation
_[_] : (M : Δ ⊢ A) (σ : Γ ⊨ Δ) → Γ ⊢ A M [ id ] = M M [ σ ↑ ] = (M [ σ ]) ↑ • [ σ ▷ P ] = P (M ↑) [ σ ▷ P ] = M [ σ ] (ƛ M) [ σ @ △ ] = ƛ (M [ σ ↑ ▷ • ]) (L · M) [ σ @ △ ] = L [ σ ] · (M [ σ ]) _⨟_ : (σ : Θ ⊨ Δ) (τ : Γ ⊨ Θ) → Γ ⊨ Δ σ ⨟ id = σ σ ⨟ (τ ↑) = (σ ⨟ τ) ↑ id ⨟ τ @ △ = τ (σ ↑) ⨟ (τ ▷ Q) = σ ⨟ τ (σ ▷ P) ⨟ τ @ △ = (σ ⨟ τ) ▷ (P [ τ ]) infixl 5 _⨟_ [][] : (M : Δ ⊢ A) (σ : Θ ⊨ Δ) (τ : Γ ⊨ Θ) → M [ σ ] [ τ ] = M [ σ ⨟ τ ] [][] M σ id = refl [][] M σ (τ ↑) = ap _↑ ([][] M σ τ) [][] M id (τ ▷ M₁) = refl [][] M (σ ↑) (τ ▷ M₁) = [][] M σ τ [][] • (σ ▷ P) τ@△ = refl [][] (M ↑) (σ ▷ P) τ@△ = [][] M σ τ [][] (ƛ N) σ@△ τ@△ = ap ƛ_ ([][] N (σ ↑ ▷ •) (τ ↑ ▷ •)) [][] (L · M) σ@△ τ@△ = cong₂ _·_ ([][] L σ τ) ([][] M σ τ) {-# REWRITE [][] #-}
Left identity
left-id : (τ : Γ ⊨ Δ) → id ⨟ τ = τ left-id id = refl left-id (τ ↑) = ap _↑ (left-id τ) left-id (τ ▷ Q) = refl {-# REWRITE left-id #-}
Associative
assoc : (σ : Θ ⊨ Δ) (τ : Ξ ⊨ Θ) (υ : Γ ⊨ Ξ) → (σ ⨟ τ) ⨟ υ = σ ⨟ (τ ⨟ υ) assoc σ τ id = refl assoc σ τ (υ ↑) = ap _↑ (assoc σ τ υ) assoc σ id (υ ▷ M) = refl assoc σ (τ ↑) (υ ▷ M) = assoc σ τ υ assoc id (τ ▷ M₁) (υ ▷ M) = refl assoc (σ ↑) (τ ▷ M₁) (υ ▷ M) = assoc σ τ (υ ▷ M) assoc (σ ▷ M₂) (τ ▷ M₁) (υ ▷ M) = cong₂ _▷_ (assoc σ (τ ▷ M₁) (υ ▷ M)) refl {-# REWRITE assoc #-}
下面的案例是本來在 PLFA 中不好做出來,但用這套就很簡單的問題
_[_]₀ : (N : Γ ▷ A ⊢ B) (M : Γ ⊢ A) ------------ → Γ ⊢ B N [ M ]₀ = N [ id ▷ M ] _[_]₁ : (N : Γ ▷ A ▷ B ⊢ C) (M : Γ ⊢ A) ------------ → Γ ▷ B ⊢ C N [ M ]₁ = N [ (id ▷ M) ↑ ▷ • ] double-subst : N [ M ]₁ [ L ]₀ = N [ L ↑ ]₀ [ M ]₀ double-subst = refl commute-subst : N [ M ]₀ [ L ]₀ = N [ L ]₁ [ M [ L ]₀ ]₀ commute-subst = refl
最後也有談到缺點是 identifying when terms are equivalent may become more difficult,但我沒有試這是什麼清況。
NOTE: Substitution Without Copy and Paste [tt-IHCF]
NOTE: Substitution Without Copy and Paste [tt-IHCF]
Substitution Without Copy and Paste
The copy-and-paste approach [ag-000M]
The copy-and-paste approach [ag-000M]
{-# OPTIONS --safe --without-K #-} module ag-000M where open import MLTT.Spartan
類型跟 context
data Ty : 𝓤₀ ̇ where base : Ty _⇒_ : Ty → Ty → Ty infixl 50 _⇒_ data Con : 𝓤₀ ̇ where ◇ : Con _▷_ : Con → Ty → Con infixl 40 _▷_
- 等一下用的變數
- de Bruijn variables
- terms
variable Γ Δ Ξ : Con A B C : Ty data _∋_ : Con → Ty → 𝓤₀ ̇ where here : Γ ▷ A ∋ A there : Γ ∋ A → (B : Ty) ------------------ → Γ ▷ B ∋ A infixl 30 _∋_ data _⊢_ : Con → Ty → 𝓤₀ ̇ where -- embeds variables in λ-terms `_ : Γ ∋ A → Γ ⊢ A -- application t · u _·_ : Γ ⊢ A ⇒ B → Γ ⊢ A → Γ ⊢ B ƛ_ : Γ ▷ A ⊢ B → Γ ⊢ A ⇒ B infixl 20 _⊢_ infixl 60 `_ infixl 50 _·_ infixl 40 ƛ_
substitution 定義成
data _⊩_ : Con → Con → 𝓤₀ ̇ where ε : Γ ⊩ ◇ _,_ : Γ ⊩ Δ → Γ ⊢ A → Γ ⊩ Δ ▷ A
現在要定義 substitution 在 terms 跟 variables 上的作用:
_v[_] : Δ ∋ A → Γ ⊩ Δ → Γ ⊢ A here v[ ts , t ] = t there i B v[ ts , t ] = i v[ ts ] data _⊩v_ : Con → Con → 𝓤₀ ̇ where ε : Γ ⊩v ◇ _,_ : Γ ⊩v Δ → Γ ∋ A → Γ ⊩v Δ ▷ A _v[_]v : Γ ∋ A → Δ ⊩v Γ → Δ ∋ A here v[ is , i ]v = i there i B v[ is , j ]v = i v[ is ]v _⁺v_ : Γ ⊩v Δ → (A : Ty) → Γ ▷ A ⊩v Δ ε ⁺v A = ε (is , i) ⁺v A = (is ⁺v A) , there i A _↑v_ : Γ ⊩v Δ → (A : Ty) → Γ ▷ A ⊩v Δ ▷ A is ↑v A = (is ⁺v A) , here _[_]v : Γ ⊢ A → Δ ⊩v Γ → Δ ⊢ A (` i) [ is ]v = ` (i v[ is ]v) (t · u) [ is ]v = (t [ is ]v) · (u [ is ]v) (ƛ t) [ is ]v = ƛ (t [ is ↑v _ ]v) idv : Γ ⊩v Γ idv {Γ = ◇} = ε idv {Γ = Γ ▷ A} = idv ↑v A
為了定義下面的 suc-tm,需要定義上面大量的類似結構
Γ ⊩v Δ
_⁺_ : Γ ⊩ Δ → (A : Ty) → Γ ▷ A ⊩ Δ ε ⁺ A = ε (ts , t) ⁺ A = (ts ⁺ A) , suc-tm t A where suc-tm : Γ ⊢ B → (A : Ty) → Γ ▷ A ⊢ B suc-tm t A = t [ idv ⁺v A ]v _↑_ : Γ ⊩ Δ → (A : Ty) → Γ ▷ A ⊩ Δ ▷ A ts ↑ A = ts ⁺ A , ` here _[_] : Γ ⊢ A → Δ ⊩ Γ → Δ ⊢ A (` i) [ ts ] = i v[ ts ] (t · u) [ ts ] = (t [ ts ]) · (u [ ts ]) (ƛ t) [ ts ] = ƛ (t [ ts ↑ _ ])
所以為了避免這些重複,方法要改成:
Substituion without copy and paste 的提議 [ag-000N]
Substituion without copy and paste 的提議 [ag-000N]
{-# OPTIONS --safe --without-K #-} module ag-000N where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) variable Γ Δ Ξ : Con A B C : Ty
引入 Sort 區分 variable 跟 term 的情況
mutual data Sort : 𝓤₀ ̇ where V : Sort T>V : (s : Sort) → IsV s → Sort data IsV : Sort → 𝓤₀ ̇ where isV : IsV V pattern T = T>V V isV variable q r s : Sort
這樣就可以把 variables 跟 terms 定義到一起,用 s 區分
Γ ⊢[ s ] A 是 variable 還是 term
data _⊢[_]_ : Con → Sort → Ty → 𝓤₀ ̇ where here : Γ ▷ A ⊢[ V ] A there : Γ ⊢[ V ] A → (B : Ty) → Γ ▷ B ⊢[ V ] A `_ : Γ ⊢[ V ] A → Γ ⊢[ T ] A _·_ : Γ ⊢[ T ] A ⇒ B → Γ ⊢[ T ] A → Γ ⊢[ T ] B ƛ_ : Γ ▷ A ⊢[ T ] B → Γ ⊢[ T ] A ⇒ B variable x y z : Γ ⊢[ q ] A
substitution 現在定義成
data _⊩[_]_ : Con → Sort → Con → 𝓤₀ ̇ where ε : Γ ⊩[ q ] ◇ _,_ : Γ ⊩[ q ] Δ → Γ ⊢[ q ] A → Γ ⊩[ q ] Δ ▷ A variable xs ys zs : Δ ⊩[ q ] Γ
現在需要考慮 sort 之間的關係,這些 lemma 有助於簡化後面的證明
data _⊑_ : Sort → Sort → Set where rfl : s ⊑ s v⊑t : V ⊑ T _⊔_ : Sort → Sort → Sort V ⊔ r = r T ⊔ r = T
一些輔助用的 REWRITE [ag-000O]
一些輔助用的 REWRITE [ag-000O]
{-# OPTIONS --without-K --rewriting #-} module ag-000O where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N {-# BUILTIN REWRITE _=_ #-}
這邊的定義很繁瑣但只是單純攤開 V、T
就能證明,並不是很重要。重點在最後用 REWRITE
避免後續需要證明一些麻煩的情況
⊑t : s ⊑ T ⊑t {V} = v⊑t ⊑t {T} = rfl v⊑ : V ⊑ s v⊑ {V} = rfl v⊑ {T} = v⊑t ⊑q⊔ : q ⊑ (q ⊔ r) ⊑q⊔ {V}{V} = rfl ⊑q⊔ {V}{T} = v⊑t ⊑q⊔ {T}{V} = rfl ⊑q⊔ {T}{T} = rfl ⊔⊔ : q ⊔ (r ⊔ s) = (q ⊔ r) ⊔ s ⊔⊔ {V}{V}{V} = refl ⊔⊔ {V}{V}{T} = refl ⊔⊔ {V}{T}{V} = refl ⊔⊔ {V}{T}{T} = refl ⊔⊔ {T}{V}{V} = refl ⊔⊔ {T}{V}{T} = refl ⊔⊔ {T}{T}{V} = refl ⊔⊔ {T}{T}{T} = refl ⊔v : q ⊔ V = q ⊔v {V} = refl ⊔v {T} = refl ⊔t : q ⊔ T = T ⊔t {V} = refl ⊔t {T} = refl ⊑⊔r : r ⊑ (q ⊔ r) ⊑⊔r {V}{V} = rfl ⊑⊔r {V}{T} = v⊑t ⊑⊔r {T}{V} = rfl ⊑⊔r {T}{T} = rfl ⊔-self : q ⊔ q = q ⊔-self {V} = refl ⊔-self {T} = refl {-# REWRITE ⊔⊔ ⊔v ⊔t ⊔-self #-}
substitution 的組合 [ag-000P]
substitution 的組合 [ag-000P]
{-# OPTIONS --without-K --rewriting #-} module ag-000P where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N open import ag-000O
這裡的目的是定義 ⊑ relation 對 term 的影響,以及定義
substitution 的結合 ◦
tm⊑ : q ⊑ s → Γ ⊢[ q ] A → Γ ⊢[ s ] A tm⊑ rfl x = x tm⊑ v⊑t i = ` i here[_] : (q : Sort) → Γ ▷ A ⊢[ q ] A here[ V ] = here here[ T ] = ` here mutual _[_] : Γ ⊢[ q ] A → Δ ⊩[ r ] Γ → Δ ⊢[ q ⊔ r ] A here [ xs , x ] = x there i _ [ xs , x ] = i [ xs ] (` i) [ xs ] = tm⊑ ⊑t (i [ xs ]) (t · u) [ xs ] = (t [ xs ]) · (u [ xs ]) (ƛ t) [ xs ] = ƛ (t [ xs ↑ _ ]) id-poly : (q : Sort) → Γ ⊩[ q ] Γ id-poly {Γ = ◇} q = ε id-poly {Γ = Γ ▷ A} q = id-poly q ↑ A id : Γ ⊩[ V ] Γ id = id-poly V {-# INLINE id #-} there[_] : (q : Sort) → Γ ⊢[ q ] B → (A : Ty) → Γ ▷ A ⊢[ q ] B there[ V ] i A = there i A there[ T ] t A = t [ id ⁺ A ] _⁺_ : Γ ⊩[ q ] Δ → (A : Ty) → Γ ▷ A ⊩[ q ] Δ ε ⁺ A = ε (ts , t) ⁺ A = (ts ⁺ A) , there[ _ ] t A _↑_ : Γ ⊩[ q ] Δ → (A : Ty) → Γ ▷ A ⊩[ q ] Δ ▷ A ts ↑ A = ts ⁺ A , here[ _ ] infixl 70 _⁺_ _◦_ : Γ ⊩[ q ] Ξ → Δ ⊩[ r ] Γ → Δ ⊩[ q ⊔ r ] Ξ ε ◦ ys = ε (xs , x) ◦ ys = (xs ◦ ys) , x [ ys ]
Proposition. The right identity law [ag-000Q]
Proposition. The right identity law [ag-000Q]
{-# OPTIONS --without-K --rewriting #-} module ag-000Q where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N open import ag-000O open import ag-000P
⁺-nat[]v : (i : Γ ⊢[ V ] A) → (xs : Δ ⊩[ q ] Γ) → i [ xs ⁺ B ] = there[ q ] (i [ xs ]) B ⁺-nat[]v here (xs , x) = refl ⁺-nat[]v (there j _) (xs , x) = ⁺-nat[]v j xs [id] : x [ id ] = x [id] {x = here} = refl [id] {x = there i B} = (i [ id ⁺ B ]) =⟨ ⁺-nat[]v {q = V} i id ⟩ there (i [ id ]) B =⟨ ap (λ - → there - B) [id] ⟩ there i B ∎ [id] {x = ` i} = ap `_ [id] [id] {x = t · u} = ((t [ id ]) · (u [ id ])) =⟨ ap (t [ id ] ·_) [id] ⟩ ((t [ id ]) · u) =⟨ ap (_· u) [id] ⟩ (t · u) ∎ [id] {x = ƛ t} = ap ƛ_ [id] ◦id : xs ◦ id = xs ◦id {xs = ε} = refl ◦id {xs = xs , x} = (xs ◦ id) , (x [ id ]) =⟨ ap ((xs ◦ id) ,_) [id] ⟩ (xs ◦ id) , x =⟨ ap (_, x) ◦id ⟩ xs , x ∎
Proposition. Left identity law 與 Associative law [ag-000R]
Proposition. Left identity law 與 Associative law [ag-000R]
{-# OPTIONS --allow-unsolved-metas --without-K --rewriting #-} module ag-000R where open import MLTT.Spartan hiding (_⊔_; id) open import ag-000M using (Ty; _⇒_; Con; ◇; _▷_) open import ag-000N open import ag-000O open import ag-000P open import ag-000Q
這兩個是 mutual 定義的,而且有一些 goals 我也看不出怎麼解了,暫時就先這樣 xd
tm[] : tm⊑ ⊑t (x [ xs ]) = (tm⊑ ⊑t x) [ xs ] tm[] {x = here} = refl tm[] {x = there x B} = refl tm[] {x = ` x} = tm[] {x = x} tm[] {x = x · x₁} = refl tm[] {x = ƛ x} = refl zero[] : {q : Sort} {r : Sort} {Γ : Con} {Δ : Con} {A : Ty} {xs : Δ ⊩[ r ] Γ} {x : Δ ⊢[ r ] A} → here[ q ] [ xs , x ] = tm⊑ (⊑⊔r {q = q}) x zero[] {q = V} {r = V} = refl zero[] {q = V} {r = T} = refl zero[] {q = T} {r = V} = refl zero[] {q = T} {r = T} = refl tm⊑zero : (q⊑r : q ⊑ r) → here[ r ] = tm⊑ q⊑r here[ q ] tm⊑zero rfl = refl tm⊑zero v⊑t = refl {-# TERMINATING #-} mutual suc[] : (there[ s ] x _) [ ys , y ] = x [ ys ] suc[] {s = V} = refl suc[] {s = T} {x = x} {ys = ys} {y = y} = there[ T ] x _ [ ys , y ] =⟨ refl ⟩ x [ id ⁺ _ ] [ ys , y ] =⟨ [◦] {x = x} ⁻¹ ⟩ x [ (id ⁺ _) ◦ (ys , y) ] =⟨ ap (x [_]) ⁺◦ ⟩ x [ id ◦ ys ] =⟨ ap (x [_]) id◦ ⟩ x [ ys ] ∎ ⁺◦ : xs ⁺ A ◦ (ys , x) = xs ◦ ys ⁺◦ {xs = ε} = refl ⁺◦ {xs = ts , t} {A = A} {ys = ys} {x = x} = ((ts ⁺ A) ◦ (ys , x)) , (there[ _ ] t A [ ys , x ]) =⟨ ap (((ts ⁺ A) ◦ (ys , x)) ,_) (suc[] {x = t}) ⟩ ((ts ⁺ A) ◦ (ys , x)) , (t [ ys ]) =⟨ ap (_, (t [ ys ])) ⁺◦ ⟩ (ts ◦ ys) , (t [ ys ]) ∎ ⁺−nat◦ : {xs : Δ ⊩[ q ] Γ} → {ys : Ξ ⊩[ r ] Δ} → {A : Ty} → xs ◦ (ys ⁺ A) = (xs ◦ ys) ⁺ A ⁺−nat◦ {xs = ε} = refl ⁺−nat◦ {q = q} {r = r} {xs = xs , x} {ys = ys} {A = A} = (xs ◦ (ys ⁺ A)) , (x [ ys ⁺ A ]) =⟨ ap ((xs ◦ (ys ⁺ A)) ,_) (⁺-nat[] {q = q} {B = A} {x = x} {xs = ys}) ⟩ (xs ◦ (ys ⁺ A)) , there[ _ ] (x [ ys ]) A =⟨ ap (_, there[ _ ] (x [ ys ]) A) ⁺−nat◦ ⟩ ((xs ◦ ys) ⁺ A) , there[ _ ] (x [ ys ]) A ∎ ⁺-nat[] : {q r : Sort} → {A B : Ty} → {x : Γ ⊢[ q ] A} → {xs : Δ ⊩[ r ] Γ} → x [ xs ⁺ B ] = there[ q ⊔ r ] (x [ xs ]) B ⁺-nat[] {q = V} {x = i} {xs = xs} = ⁺-nat[]v i xs ⁺-nat[] {q = T} {B = B} {x = x} {xs = xs} = x [ xs ⁺ B ] =⟨ ap (λ - → x [ - ⁺ B ]) (◦id {xs = xs} ⁻¹) ⟩ x [ (xs ◦ id) ⁺ B ] =⟨ ap (x [_]) (⁺−nat◦ ⁻¹) ⟩ x [ xs ◦ (id ⁺ B) ] =⟨ [◦] {x = x} ⟩ x [ xs ] [ id ⁺ B ] =⟨ refl ⟩ there[ T ] (x [ xs ]) B ∎ ↑◦ : {r s : Sort} → {xs : Δ ⊩[ r ] Ξ} → {ys : Γ ⊩[ s ] Δ} → {A : Ty} → (xs ◦ ys) ↑ A = (xs ↑ A) ◦ (ys ↑ A) ↑◦ {r = r} {s = s} {xs = xs} {ys = ys} {A = A} = (xs ◦ ys) ↑ A =⟨ refl ⟩ (xs ◦ ys) ⁺ A , here[ r ⊔ s ] =⟨ ap (λ - → - , here[ _ ]) (⁺−nat◦ ⁻¹) ⟩ xs ◦ (ys ⁺ A) , here[ r ⊔ s ] =⟨ ap (xs ◦ (ys ⁺ A) ,_) (tm⊑zero (⊑⊔r {r = s} {q = r})) ⟩ xs ◦ (ys ⁺ A) , tm⊑ (⊑⊔r {q = r}) here[ s ] =⟨ ap (xs ◦ (ys ⁺ A) ,_) (zero[] {q = r} {r = s} {A = A} {xs = ys ⁺ A} {x = here[ s ]} ⁻¹) ⟩ xs ◦ (ys ⁺ A) , (here[ r ] [ ys ↑ A ]) =⟨ ap (_, (here[ r ] [ ys ↑ A ])) (⁺◦ {xs = xs} {A = A} {ys = ys ⁺ A} {x = here[ s ]} ⁻¹) ⟩ ((xs ⁺ A) ◦ (ys ⁺ A , here[ s ])) , (here[ r ] [ ys ↑ A ]) =⟨ refl ⟩ (xs ↑ A) ◦ (ys ↑ A)∎ [◦] : x [ xs ◦ ys ] = x [ xs ] [ ys ] [◦] {x = here} {xs = xs , x} = refl [◦] {x = there i B} {xs = xs , x} = [◦] {x = i} [◦] {x = ` x} {xs = xs} {ys = ys} = tm⊑ ⊑t (x [ xs ◦ ys ]) =⟨ ap (λ - → tm⊑ ⊑t -) ([◦] {x = x}) ⟩ tm⊑ ⊑t (x [ xs ] [ ys ]) =⟨ tm[] {x = x [ xs ]} ⟩ (tm⊑ ⊑t (x [ xs ]) [ ys ]) ∎ [◦] {x = t · u} {xs = xs} {ys = ys} = (t [ xs ◦ ys ]) · (u [ xs ◦ ys ]) =⟨ ap (_· (u [ xs ◦ ys ])) ([◦] {x = t}) ⟩ (t [ xs ] [ ys ]) · (u [ xs ◦ ys ]) =⟨ ap ((t [ xs ] [ ys ]) ·_) ([◦] {x = u}) ⟩ ((t [ xs ]) [ ys ]) · ((u [ xs ]) [ ys ]) ∎ [◦] {x = ƛ t} {xs = xs} {ys = ys} = ap ƛ_ (t [ (xs ◦ ys) ↑ _ ] =⟨ ap (t [_]) (↑◦ {xs = xs}) ⟩ t [ (xs ↑ _) ◦ (ys ↑ _) ] =⟨ [◦] {x = t} ⟩ (t [ xs ↑ _ ]) [ ys ↑ _ ] ∎) id◦' : Sort → id ◦ xs = xs id◦' {xs = ε} q = refl id◦' {xs = xs , x} q = ap (_, x) (((id ⁺ _) ◦ (xs , x)) =⟨ ⁺◦ ⟩ id ◦ xs =⟨ id◦ ⟩ xs ∎) id◦ : id ◦ xs = xs id◦ = id◦' V {-# INLINE id◦ #-}
到這裡已經證明了 contexts 與 substitutions 真的是一個範疇,而且這個範疇有 terminal object。第五節是把這邊的工作放進去 CwF-simple(constant presheaves 可以讓 CwF 適用於 simply typed calculus)裡,那個我暫時沒什麼興趣。
AI Is Slowly Destroying Your Brain [45VG]
AI Is Slowly Destroying Your Brain [45VG]
新增一些心理學研究結果作為思考 現代 - 商業、科技與政治交織的空間 的案例。
Lie 群的意義 [VQ6V]
Lie 群的意義 [VQ6V]
Lie 群是同時是群跟流形的物件,但這有什麼意義呢?
最簡單的案例是平面旋轉群 ,這是由所有平面上的旋轉組成的群,如果把所有的軌跡都畫到平面上,那這會構成一個 。而我們知道局部的看 可以視為一個直線(切線),這就使得局部的來說,可以用切線近似的討論,這條線被稱為 Lie algebra。

所以我們成功地把曲線問題變成線性問題,更重要的是,這個方法更廣泛來說還是有用,比如很多物理學研究的對稱性可以用某個 Lie 群研究。
另外很有趣的是,Complex number 除了可以用代數的方式定義(see Algebra: Chapter 0, III, Proposition 4.6.):
在 Naive Lie Theory 中提到我們也能用旋轉矩陣來定義。
Lawvere-Tierney topology [math-MRL4]
Lawvere-Tierney topology [math-MRL4]
Let be a topos. A Lawvere-Tierney topology in is a morphism such that the following diagrams are commutative:
A topology in a topos gives rise to a new topos defined over .
Tool. x86-64 Playground [software-9JPJ]
Tool. x86-64 Playground [software-9JPJ]
Definition. Weil algebra [math-T4B2]
Definition. Weil algebra [math-T4B2]
A Weil algebra is an algebra over the rational numbers , equipped with a morphism
such that is a local ring with maximal ideal:
with a nilpotent ideal, and such that is a finite dimensional -vector space.
The notion of Weil algebra makes sense in any topos with a natural numbers object .
Proposition. nilpotent maps form a prime ideal [math-6W2V]
Proposition. nilpotent maps form a prime ideal [math-6W2V]
Definition. Coprimary [local-0]
Definition. Coprimary [local-0]
Let be a Noetherian ring. A nonzero finitely generated -module is coprimary if for all , the multiplication map (reuse element to denote it)
is injective or nilpotent.
If is coprimary, then the set
forms a prime ideal in .
Proof. [local-1]
Proof. [local-1]
To check is a prime ideal, we want to check that if and then .
Because is coprimary, so such are injective, and
the composition of injective maps is injective, hence . □
具體的 Sheaf 以及如何得到 ringed 與 locally ringed space 的定義 [UXEP]
具體的 Sheaf 以及如何得到 ringed 與 locally ringed space 的定義 [UXEP]
Sheaf 的定義是
Definition. Sheaf [math-PPAW]
Definition. Sheaf [math-PPAW]
我們說一個 presheaf 是 sheaf 是指:對所有 open sets in 與所有 的 open covering ,以下兩個條件成立
- Let with for all . Then .
- Given for all such that for all . Then there exists an such that (注意,根據條件一這個 是唯一的)
對我個人比較有意義的案例是
Example. 上的可微分函數 [local-0]
Example. 上的可微分函數 [local-0]
假設 是一個 -manifold(),我們通常用 表示集合
,而 是 的一個開集。這時候 是一個 sheaf of -algebras on
- 這本身也是一個 Ring
- 在這個案例中,stalk 也就變成經典的 function germs(用重合定義的函數局部等價類)。
所以 ringed space 也就定義成了
Definition. Ringed space [math-9M06]
Definition. Ringed space [math-9M06]
Ringed space 是一個 pair
- 一個 topological space
- 一個 sheaf of (commutative) rings
注意到如果 是一個 commutative ring,那 -algebra 也能視為一個 ring (with unit),所以這確實是 manifold 的推廣。
如果進一步要求 的每個 stalk 都是 local ring,那就得到了 locally ringed space:
Definition. Locally Ringed space [math-AYGI]
Definition. Locally Ringed space [math-AYGI]
Locally ringed space 是 ringed space 加上條件:for all
是一個 local ring(i.e. 有 maximal ideal)
語法作為一種檢視方式 [32PV]
語法作為一種檢視方式 [32PV]
正如 Bicameral, Not Homoiconic 一文所述(推薦先看完 Bicameral 再看我這裡寫的東西),真正讓 LISP 脫穎而出的功能,是它 pipeline 特殊的雙層解析器:
- scan 出詞素(token)
- 用 reader 讀出「資料」,通常是一種 form,以 LISP 來說就是 s-expression。而且 reader 會順便讀取 macro 定義跟把 macro 展開
- 最後用 parser 解析成表面語言
根據程式語言的設計會影響實現,有些實現方式會非常多的靜態檢查,以至於在這些實現內部消除了絕大多數的語意錯誤,像是 dependent typed 的語言,這時候我們幾乎可以相信這些編譯器的內部表示跟我們等下提到的客觀語法真的一樣。要注意這並不總是成立,也有很多語意錯誤會被延遲到執行時再處理(如 Python、Racket 的情況),所以在程式語言的實現中,總是假設並依賴一個理想的客觀語法,是由我們規定的語意生成的,我們通常用化簡語意或是指稱語意去研究,而編譯器很大一部分工作就是保證遵循這個語意來實現語言。一套客觀語法可以有很多種檢視方式,比如「指定 a 的新值是整數 1」這個客觀語法可以寫成
- Racket
(set-box! a 1) - C
a = 1; - OCaml
a := 1
更瘋狂一點的話,也不是不能寫成 JSON
{
"assign": {
"variable": "a",
"expression": {
"type": "int",
"val": 1
}
}
}
為什麼表面語法有可能是錯的呢?比如 OCaml 的 parser 不會拒絕 a := 1 的寫法,即使 a 不是 int ref 類型。要到 type checker 的檢查階段,這段程式碼才會因為類型錯誤而被拒絕(這樣就消除了一個語意不正確的表面語句)。
所以一般開發者說的語法,其實可以說是「檢視語法」,當然這並不是說檢視不重要,正如 Concrete syntax matters, actually 說的,好的檢視方式本身就揭示了我們在談論什麼:我當然可以用 * 表示加法、用 + 表示乘法,然後問 3 + 2 * 5 是什麼,但如果有人算錯,我不應該太意外。
所以之所以要視之為檢視,是因為要讓我們可以去想像更好的表示方式,比如
「檢視」暗示了更豐富的運用,像在 proof assistant 的應用中,我們經常想要知道當前 context 可以看到的定義,以及打算證明的目標的類型;在除錯時我們想看到執行期的堆疊等等,都可以考慮為與跟生成客觀語法的語意匹配的檢視方式。
最後,釐清一些常見的誤解
- Bicameral 語法不一定要是 s-expression: Rhombus 使用 Shrubbery Notation
- 不是所有 LISPy 語言都用 list 表示其資料層,Racket 就用了 syntax object 抽象(Bicameral 一文也有說這件事)
MILKY☆SUBWAY [TDJD]
MILKY☆SUBWAY [TDJD]
In Defense of Inefficiency [29QD]
In Defense of Inefficiency [29QD]
Я - extremely composable embeddable programming language [software-000A]
Я - extremely composable embeddable programming language [software-000A]
Extremely composable embeddable programming language
可以先從這些截圖感受一下這什麼程式語言xd



Tool. witr - Why is this running? [software-0009]
Tool. witr - Why is this running? [software-0009]
系統上執行的某個程式或服務 - 無論是 process、service 或綁定到連接埠的程式。都必然有其原因,但這些原因通常間接、不易察覺,或是跨越多個層級,例如監控程式、容器、服務或 shell。而 witr 的用途就是一次展示這些資訊。
Tool. OCaml formatter online configurator [programming-0006]
Tool. OCaml formatter online configurator [programming-0006]
看不懂 OCaml formatter 要怎麼設定?這個專案把排版選項、原始碼跟結果都展示出來,讓人直覺的做出選擇。
Definition. Covering spaces in HoTT [ag-000L]
Definition. Covering spaces in HoTT [ag-000L]
A covering space of a type (space) is a family of sets indexed by .
{-# OPTIONS --safe --without-K #-} module ag-000L where open import MLTT.Spartan hiding (fiber) open import UF.Sets record covering (A : 𝓤 ̇ ) : 𝓤 ⁺ ̇ where constructor cov[_,_] field fiber : A → 𝓤 ̇ fiber-is-set : ∀ (a : A) → is-set (fiber a)
From Zero to QED [lean-0000]
From Zero to QED [lean-0000]
https://sdiehl.github.io/zero-to-qed/01_introduction.html 這個專案教了很多很細節的 tactics,是很好的參考工具。
Eliminator [ag-000K]
Eliminator [ag-000K]
{-# OPTIONS --safe --without-K #-} module ag-000K where open import MLTT.Spartan open import Naturals.Properties
Eliminator of ℕ
ℕ-elim : ∀ (P : ℕ → 𝓤 ̇) → P 0 → (∀ (n : ℕ) → P n → P (succ n)) → (∀ (n : ℕ) → P n) ℕ-elim P P0 Ps zero = P0 ℕ-elim P P0 Ps (succ n) = Ps n (ℕ-elim P P0 Ps n)
Define with pattern matching
plus : ℕ → ℕ → ℕ plus zero b = b plus (succ a) b = succ (plus a b) mul : ℕ → ℕ → ℕ mul zero c = zero mul (succ a) b = plus b (mul a b) exp : ℕ → ℕ → ℕ exp x zero = 1 exp x (succ k) = mul x (exp x k)
Now use the eliminator to define them
plus' : ℕ → ℕ → ℕ plus' x = ℕ-elim (λ _ → ℕ → ℕ) (λ z → z) (λ x' plus-x' → λ y → succ (plus-x' y)) x t5 : plus' 1 1 = 2 t5 = refl p1 : (a b : ℕ) → plus a b = plus' a b p1 zero b = refl p1 (succ a) b = succ (plus a b) =⟨ ap succ (p1 a b) ⟩ succ (plus' a b) =⟨by-definition⟩ succ (ℕ-elim (λ _ → ℕ → ℕ) (λ z → z) (λ x' plus-x' → λ y → succ (plus-x' y)) a b) =⟨by-definition⟩ plus' (succ a) b ∎ mul' : ℕ → ℕ → ℕ mul' x = ℕ-elim (λ _ → ℕ → ℕ) (λ z → zero) (λ x' mul-x' → λ y → plus' y (mul-x' y)) x t7 : mul' 0 1 = 0 t7 = refl t8 : mul' 1 1 = 1 t8 = refl t9 : mul' 2 2 = 4 t9 = refl p2 : (a b : ℕ) → mul a b = mul' a b p2 zero b = refl p2 (succ a) zero = p2 a 0 p2 (succ a) (succ b) = plus (succ b) (mul a (succ b)) =⟨ p1 (succ b) (mul a (succ b)) ⟩ plus' (succ b) (mul a (succ b)) =⟨ ap (plus' (succ b)) (p2 a (succ b)) ⟩ plus' (succ b) (mul' a (succ b)) =⟨by-definition⟩ mul' (succ a) (succ b) ∎ exp' : ℕ → ℕ → ℕ exp' x y = ℕ-elim (λ _ → ℕ → ℕ) (λ x → 1) (λ y' exp-y' → λ x → mul' x (exp-y' x)) y x t10 : exp' 2 0 = 1 t10 = refl t11 : exp' 2 10 = 1024 t11 = refl p3 : (a b : ℕ) → exp a b = exp' a b p3 a zero = refl p3 zero (succ b) = refl p3 (succ a) (succ b) = exp (succ a) (succ b) =⟨by-definition⟩ mul (succ a) (exp (succ a) b) =⟨ p2 (succ a) (exp (succ a) b) ⟩ mul' (succ a) (exp (succ a) b) =⟨ ap (mul' (succ a)) (p3 (succ a) b) ⟩ mul' (succ a) (exp' (succ a) b) =⟨by-definition⟩ exp' (succ a) (succ b) ∎
Plus commutative yoga
C : commutative plus C zero zero = refl C zero (succ b) = succ b =⟨ ap succ (C 0 b) ⟩ succ (plus b zero) ∎ C (succ a) zero = succ (plus a 0) =⟨ ap succ (C a 0) ⟩ succ (plus 0 a) =⟨ refl ⟩ plus 0 (succ a) ∎ C (succ a) (succ b) = succ (plus a (succ b)) =⟨ ap succ (C a (succ b)) ⟩ succ (plus (succ b) a) =⟨ ap succ refl ⟩ succ (succ (plus b a)) =⟨ ap (λ x → succ (succ x)) (C b a) ⟩ succ (succ (plus a b)) =⟨ ap succ refl ⟩ succ (plus (succ a) b) =⟨ ap succ (C (succ a) b) ⟩ succ (plus b (succ a)) ∎
Remind
add1 : ℕ → ℕ add1 = ℕ-elim (λ _ → ℕ) (succ zero) λ _ n → succ n t1 : add1 0 = 1 t1 = refl double' : ℕ → ℕ double' = ℕ-elim (λ _ → ℕ) zero λ _ mn → succ (succ mn) t2 : double' 0 = 0 t2 = refl t3 : double' 1 = 2 t3 = refl t4 : double' 2 = 4 t4 = refl
M-type (the type of non-well-founded, labelled trees) [ag-000J]
M-type (the type of non-well-founded, labelled trees) [ag-000J]
{-# OPTIONS --cubical --guardedness --two-level --no-level-universe #-} module ag-000J where open import Cubical.Foundations.Prelude open import Cubical.Data.Sum open import Cubical.Data.Nat data 𝟘 : Type where data 𝟙 : Type where ⋆ : 𝟙 data Maybe (X : Type) : Type where none : Maybe X some : X → Maybe X record ℕ∞ : Type where coinductive field pred∞ : Maybe ℕ∞
M-type 是 non-well-formed, labelled trees
的型別,有可能有有限也可能有無限長的 path。 M 是 strictly
positive coinductive types 的 universal type。
record M (S : Type) (P : S → Type) : Type where coinductive field shape : S pos : P shape → M S P
M S P 代表了 conatural number
module conatural-number where open ℕ∞ open M S = 𝟙 ⊎ 𝟙 P : S → Type P (inl _) = 𝟘 P (inr _) = 𝟙 N∞ = M S P inf : ℕ∞ pred∞ inf = none inf' : ℕ∞ pred∞ inf' = some inf i : N∞ shape i = inl ⋆ pos i = λ () i' : N∞ shape i' = inr ⋆ pos i' = λ x → i
W-type (the type of well-founded, labelled trees) [ag-000I]
W-type (the type of well-founded, labelled trees) [ag-000I]
{-# OPTIONS --cubical --guardedness --two-level --no-level-universe #-} module ag-000I where open import Cubical.Foundations.Prelude open import Cubical.Data.Sum open import Cubical.Data.Nat data 𝟘 : Type where data 𝟙 : Type where ⋆ : 𝟙
W-type (due to Martin-Löf) 是 well-founded, labelled
trees 的型別。每棵 W-type 的樹都可以有無限多分支,但 path
都是有限長。W 有兩個參數
S : Type表示 shapeP : S → Type表示有(P s)-many positions
W 是 strictly positive inductive types 的 universal
type。
data W (S : Type) (P : S → Type) : Type where sup-W : (s : S) → (P s → W S P) → W S P
Example: 自然數
module natural-number where S = 𝟙 ⊎ 𝟙 P : S → Type P (inl _) = 𝟘 -- therefore, in this direction cannot go further P (inr _) = 𝟙 -- this direction has one continuation N = W S P z : N z = sup-W (inl ⋆) λ () s : N → N s n = sup-W (inr ⋆) λ ⋆ → n α : ℕ → N α zero = z α (suc n) = s (α n) β : N → ℕ β (sup-W (inl ⋆) x) = zero β (sup-W (inr ⋆) f) = suc (β (f ⋆)) main : (n : ℕ) → β (α n) ≡ n main zero = β (α zero) ≡⟨ refl ⟩ β z ≡⟨ refl ⟩ zero ∎ main (suc n) = cong suc (main n) main⁻¹ : (n : N) → α (β n) ≡ n main⁻¹ (sup-W (inl ⋆) f) = α (β (sup-W (inl ⋆) f)) ≡⟨ refl ⟩ z ≡⟨ refl ⟩ sup-W (inl ⋆) (λ ()) ≡⟨ cong (sup-W (inl ⋆)) (sym (funExt λ ())) ⟩ sup-W (inl ⋆) f ∎ main⁻¹ (sup-W (inr ⋆) f) = α (β (sup-W (inr ⋆) f)) ≡⟨ refl ⟩ α (suc (β (f ⋆))) ≡⟨ refl ⟩ s (α (β (f ⋆))) ≡⟨ refl ⟩ sup-W (inr ⋆) (λ _ → α (β (f ⋆))) ≡⟨ cong (sup-W (inr ⋆)) (funExt t) ⟩ sup-W (inr ⋆) f ∎ where t : (x : 𝟙) → α (β (f ⋆)) ≡ f x t ⋆ = main⁻¹ (f ⋆)
Simplex category 與 face maps [math-001I]
Simplex category 與 face maps [math-001I]
根據定義,每個 simplicial set 都是 simplex category 的一個 presheaf
Definition. Simplex Category [local-0]
Definition. Simplex Category [local-0]
- Ob: 每個 object 都是 並帶有整數的 order 結構(其中 是非負整數)
- Hom: 每個 morphism 都是嚴格遞增函數
這些 morphism 可以用一類特殊的 maps 組出來,叫做 face maps,舉例來說
這個定義乍一看實在沒辦法理解這在定義什麼,所以要實際看看幾個案例:從 到 可以畫成
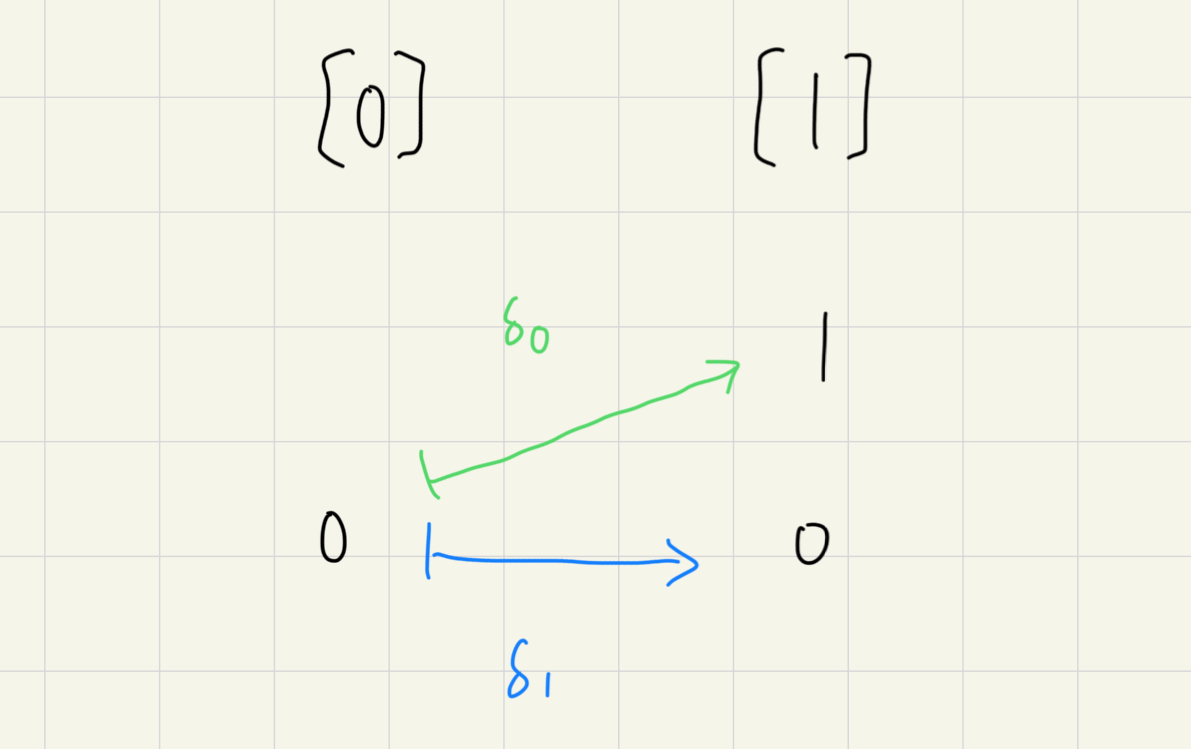
從 到 可以畫成
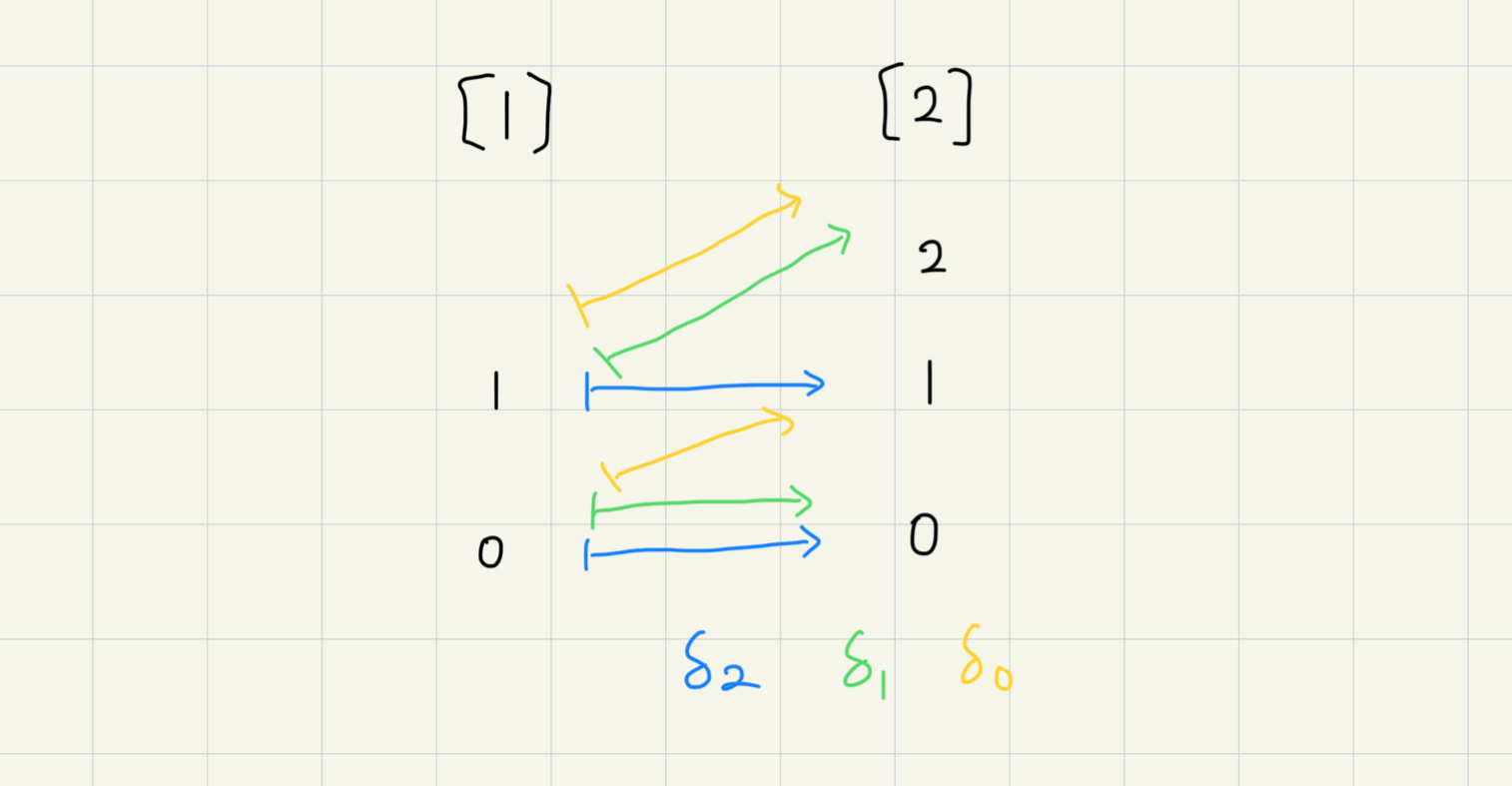
事實上,如果畫成 simplex 的幾何表示 就更明顯了:
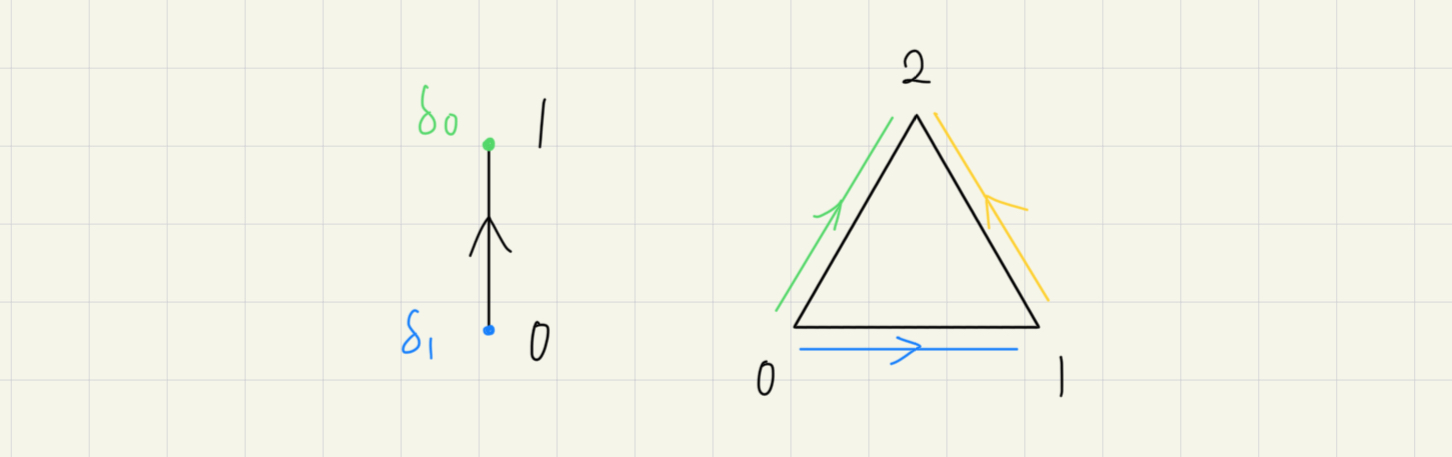
標準 -simplex 可以定義成:
所以 face maps 就是在表示 表示 的哪一個邊界,線的邊界是兩個點,面的邊界是三條線。
沒有內接矩形的平面曲線 [math-001H]
沒有內接矩形的平面曲線 [math-001H]
在看過
之後的一點嘗試。
就我的認知,有限多的 singular points 無法破壞這裡的拓墣特性,所以討論非碎形曲線的時候,頂多討論能夠減少內接矩形到什麼程度。所以我真正有興趣的是局部構成沒有內接矩形時,如何重複這個構成還是保持特性。
然而一次跨出這步太超出我目前所知了,所以只能先考慮相關的變形問題:首先,開放的曲線可能沒有內接矩形,比如下圖由兩個有界直線構成(箭頭表示無限延伸方向)
- 如果選擇了頂點與其中一邊的點,那麼法向只能再跟此圖交於一點,無法構成矩形。另一邊因為對稱性所以一樣。
- 如果選擇一邊的兩點,那法向接觸到另一邊的長度不同,自然也不是矩形。
- 如果一邊各自選一點,因為這條邊往任意一邊移動都會改變長度,也沒辦法構成矩形。
但這張圖如果稍作修改,比如加一個直線拉回來變成三角形,就會再次有內接矩形。
另一種值得考慮的基本構造是圓,因為可以說圓的內接矩形有無限多個,但也可以說某種程度上只有一個內接矩形。所以如果考慮取半圓形,另一半則是想辦法破壞對稱性,比如我考慮過的其中一種形狀是

想法就是一直取一半直徑的半圓去填右半部。這個旋轉一下就可以弄成方程組,所以要驗證這個圖形可以嘗試看看方程組中出現矩形要怎麼驗證。
Formal Topology in UF [math-001G]
Formal Topology in UF [math-001G]
Reading https://github.com/ayberkt/formal-topology-in-UF and use TypeTopology to understand
Definition. Poset [ag-000F]
Definition. Poset [ag-000F]
{-# OPTIONS --safe --without-K #-} module ag-000F where open import MLTT.Spartan open import UF.Sets open import UF.SubtypeClassifier
Order is a binary relation ≤.
order-structure : 𝓤 ̇ → 𝓤 ⁺ ̇ order-structure {𝓤} A = A → A → Ω 𝓤
A poset A is a pair (A, ≤ )
- x ≤ x for all x ∈ A
- x ≤ y and y ≤ z implies x ≤ z for all x, y, z ∈ A
- x ≤ y and y ≤ x implies x = y for all x, y ∈ A
poset-axioms : (A : 𝓤 ̇ ) → order-structure A → 𝓤 ̇ poset-axioms A _≤_ = is-set A × ((x : A) → (x ≤ x) holds) × ((x y z : A) → (x ≤ y) holds → (y ≤ z) holds → (x ≤ z) holds) × ((x y : A) → (x ≤ y) holds → (y ≤ x) holds → x = y) Poset-structure : 𝓤 ̇ → 𝓤 ⁺ ̇ Poset-structure A = Σ _≤_ ꞉ order-structure A , (poset-axioms A _≤_) Poset : (𝓤 : Universe) → 𝓤 ⁺ ̇ Poset 𝓤 = Σ A ꞉ 𝓤 ̇ , Poset-structure A
We can add a helper to extract underlying set
⟨_⟩ : {S : 𝓤 ̇ → 𝓥 ̇ } → Σ S → 𝓤 ̇ ⟨ X , s ⟩ = X order-of : (P : Poset 𝓤) → ⟨ P ⟩ → ⟨ P ⟩ → Ω 𝓤 order-of (X , _≤_ , _) x y = x ≤ y syntax order-of P x y = x ≤⟨ P ⟩ y posets-are-sets : (P : Poset 𝓤) → is-set ⟨ P ⟩ posets-are-sets (X , _≤_ , i , rfl , trans , ir) = i
A hom from a poset to another, is a map that preserves the order
is-hom : (P : Poset 𝓤) (Q : Poset 𝓥) → (⟨ P ⟩ → ⟨ Q ⟩) → 𝓤 ⊔ 𝓥 ̇ is-hom P Q f = ∀ {x y} → (x ≤⟨ P ⟩ y) holds → (f x ≤⟨ Q ⟩ f y) holds
Identity map is a hom
id-is-hom : (P : Poset 𝓤) → is-hom P P id id-is-hom P x≤y = x≤y
The composition of homs is a hom
∘-is-hom : (P : Poset 𝓤) (Q : Poset 𝓥) (R : Poset 𝓦) (f : ⟨ P ⟩ → ⟨ Q ⟩) (g : ⟨ Q ⟩ → ⟨ R ⟩) → is-hom P Q f → is-hom Q R g → is-hom P R (g ∘ f) ∘-is-hom P Q R f g f-is-hom g-is-hom x≤y = g-is-hom (f-is-hom x≤y)
Definition. Frame [ag-000G]
Definition. Frame [ag-000G]
{-# OPTIONS --safe --without-K #-} module ag-000G where open import MLTT.Spartan open import UF.SubtypeClassifier open import ag-000F
To build frame, we must be able to talk about arbitrary subsets of underlying set X
Fam : 𝓤 ̇ → 𝓤 ⁺ ̇ Fam {𝓤} A = Σ I ꞉ 𝓤 ̇ , (I → A) module JoinStntax {A : 𝓤 ̇ } (join : Fam A → A) where join-of : {I : 𝓤 ̇ } → (I → A) → A join-of {I} f = join (I , f) syntax join-of (λ i → e) = ∨⟨ i ⟩ e index : {X : 𝓤 ̇ } → Fam X → 𝓤 ̇ index (I , _) = I _$_ : {X : 𝓤 ̇ } → (F : Fam X) → index F → X _$_ (_ , f) = f infixl 40 _$_ _∈_ : {X : 𝓤 ̇ } → X → Fam X → 𝓤 ̇ x ∈ (_ , f) = fiber f x
Beside poset axioms, frame axioms are
- There is a top element ⊤, every element x ≤ ⊤
- Binary meet x ∧ y is smaller than x and y, and it is a limit
- Each arbitrary subset U has a join ∨U, such that each element of it smaller than the join
- Binary meets must distribute over arbitrary joins
frame-axioms : (X : 𝓤 ̇ ) → order-structure X → X → (X → X → X) → (Fam X → X) → 𝓤 ⁺ ̇ frame-axioms X _≤_ ⊤ _∧_ ∨ = ((x : X) → (x ≤ ⊤) holds) × ((x y : X) → ((x ∧ y) ≤ x) holds × ((x ∧ y) ≤ y) holds) × ((x y z : X) → (z ≤ x) holds → (z ≤ y) holds → (z ≤ (x ∧ y)) holds) × ((U : Fam X) → (x : X) → x ∈ U → (x ≤ ∨ U) holds) × ((U : Fam X) → (x : X) → ((y : X) → y ∈ U → (y ≤ x) holds) → (∨ U ≤ x) holds) × distrib where open JoinStntax ∨ distrib = ((U : Fam X) → (x : X) → x ∧ (∨ U) = ∨⟨ i ⟩ (x ∧ U $ i)) Frame-structure : 𝓤 ̇ → 𝓤 ⁺ ̇ Frame-structure X = Σ _≤_ ꞉ order-structure X , Σ ⊤ ꞉ X , Σ _∧_ ꞉ (X → X → X) , Σ ∨ ꞉ (Fam X → X) , (poset-axioms X _≤_) × (frame-axioms X _≤_ ⊤ _∧_ ∨) Frame : (𝓤 : Universe) → 𝓤 ⁺ ̇ Frame 𝓤 = Σ X ꞉ 𝓤 ̇ , Frame-structure X
Properties of frames [ag-000H]
Properties of frames [ag-000H]
{-# OPTIONS --safe --without-K #-} module ag-000H where open import MLTT.Spartan open import UF.SubtypeClassifier open import ag-000F open import ag-000G
In frames, meet is commutative, hence no difference between x ∧ y and y ∧ x
meet-is-comm : (F : Frame 𝓤) → (x y : ⟨ F ⟩) → 𝓤 ̇ meet-is-comm (X , _≤_ , ⊤ , _∧_ , _ ) x y = x ∧ y = y ∧ x prove-meet-is-comm : (F : Frame 𝓤) → (x y : ⟨ F ⟩) → meet-is-comm F x y prove-meet-is-comm (X , _≤_ , ⊤ , _∧_ , ∨ , (_ , _ , _ , split) , (_ , meet , lim , _ , _) ) x y = split (x ∧ y) (y ∧ x) I II where I : ((x ∧ y) ≤ (y ∧ x)) holds I = lim y x (x ∧ y) (meet x y .pr₂) (meet x y .pr₁) II : ((y ∧ x) ≤ (x ∧ y)) holds II = lim x y (y ∧ x) (meet y x .pr₂) (meet y x .pr₁)
Matrix representation of complex numbers [math-001F]
Matrix representation of complex numbers [math-001F]
To see why
behave same as the complex numbers is to write as a linear combination:
and hence we are wondering, what if we define
and multiplication as matrix multiplication, addition as matrix addition? Are these behave same as complex numbers? Since is the identity matrix, we simply get followings
we would like to know if :
as desired. Then we also know linear combinations based on and maps to complex numbers bijectively:
so now we can see this indeed is a representation of complex numbers.
旋轉矩陣的 product 是給定角度的相加 [ag-000E]
旋轉矩陣的 product 是給定角度的相加 [ag-000E]
{-# OPTIONS --without-K #-} module ag-000E where open import MLTT.Spartan hiding (_+_; _×_) open import MLTT.Fin
因為不想引入太多其餘結構,把實數跟三角函數的一些性質直接公理化來用
module _ (ℝ : 𝓤₀ ̇) where variable a b : ℝ postulate cos : ℝ → ℝ sin : ℝ → ℝ -_ : ℝ → ℝ _+_ : ℝ → ℝ → ℝ _×_ : ℝ → ℝ → ℝ tri1 : cos (a + b) = cos a × cos b + - (sin a × sin b) tri2 : sin (a + b) = sin a × cos b + sin b × cos a ℝ-neg-1 : a × - b = - (a × b) ℝ-neg-add : - a + - b = - (a + b) ℝ-+-comm : a + b = b + a ℝ-×-comm : a × b = b × a infixl 60 -_ infixl 40 _+_ infixl 50 _×_ ℝ-neg-2 : - a × b = - (a × b) ℝ-neg-2 {a}{b} = - a × b =⟨ ℝ-×-comm ⟩ b × - a =⟨ ℝ-neg-1 ⟩ - (b × a) =⟨ ap -_ ℝ-×-comm ⟩ - (a × b) ∎
矩陣可以看成由兩個索引指向某其 Field K 的元素的型別
Matrix : (m n : ℕ) → (K : 𝓤 ̇) → 𝓤 ̇ Matrix m n K = Fin m → Fin n → K
只定義 2 × 2 的矩陣乘法
_⊗_ : Matrix 2 2 ℝ → Matrix 2 2 ℝ → Matrix 2 2 ℝ _⊗_ m n 𝟎 𝟎 = m 𝟎 𝟎 × n 𝟎 𝟎 + m 𝟎 𝟏 × n 𝟏 𝟎 _⊗_ m n 𝟎 𝟏 = m 𝟎 𝟎 × n 𝟎 𝟏 + m 𝟎 𝟏 × n 𝟏 𝟏 _⊗_ m n 𝟏 𝟎 = m 𝟏 𝟎 × n 𝟎 𝟎 + m 𝟏 𝟏 × n 𝟏 𝟎 _⊗_ m n 𝟏 𝟏 = m 𝟏 𝟎 × n 𝟎 𝟏 + m 𝟏 𝟏 × n 𝟏 𝟏 infixl 30 _⊗_
旋轉矩陣它本人,這個用來表示 Rθ,其中 θ ∈ ℝ 是角度的值
R : ℝ → Matrix 2 2 ℝ R θ 𝟎 𝟎 = cos θ R θ 𝟎 𝟏 = sin θ R θ 𝟏 𝟎 = - sin θ R θ 𝟏 𝟏 = cos θ
證明目標:RθRφ = Rθ + φ
證明方式就是按 component 去證明等式成立。
thm : {θ φ : ℝ} (i j : Fin 2) → (R θ ⊗ R φ) i j = R (θ + φ) i j thm {θ}{φ} 𝟎 𝟎 = (R θ ⊗ R φ) 𝟎 𝟎 =⟨by-definition⟩ cos θ × cos φ + sin θ × (- sin φ) =⟨ ap (cos θ × cos φ +_) ℝ-neg-1 ⟩ cos θ × cos φ + - (sin θ × sin φ) =⟨ tri1 ⁻¹ ⟩ cos (θ + φ) =⟨by-definition⟩ R (θ + φ) 𝟎 𝟎 ∎ thm {θ}{φ} 𝟎 𝟏 = (R θ ⊗ R φ) 𝟎 𝟏 =⟨by-definition⟩ cos θ × sin φ + sin θ × cos φ =⟨ ℝ-+-comm ⟩ sin θ × cos φ + cos θ × sin φ =⟨ ap (sin θ × cos φ +_) ℝ-×-comm ⟩ sin θ × cos φ + sin φ × cos θ =⟨ tri2 ⁻¹ ⟩ sin (θ + φ) =⟨by-definition⟩ R (θ + φ) 𝟎 𝟏 ∎ thm {θ}{φ} 𝟏 𝟎 = (R θ ⊗ R φ) 𝟏 𝟎 =⟨by-definition⟩ (- sin θ) × cos φ + cos θ × (- sin φ) =⟨ ap (_+ cos θ × - sin φ) ℝ-neg-2 ⟩ - (sin θ × cos φ) + cos θ × (- sin φ) =⟨ ap (- (sin θ × cos φ) +_) ℝ-neg-1 ⟩ - (sin θ × cos φ) + - (cos θ × sin φ) =⟨ ℝ-neg-add ⟩ - (sin θ × cos φ + cos θ × sin φ) =⟨ ap -_ (ap (sin θ × cos φ +_) ℝ-×-comm) ⟩ - (sin θ × cos φ + sin φ × cos θ) =⟨ ap -_ (tri2 ⁻¹) ⟩ - sin (θ + φ) =⟨by-definition⟩ R (θ + φ) 𝟏 𝟎 ∎ thm {θ}{φ} 𝟏 𝟏 = (R θ ⊗ R φ) 𝟏 𝟏 =⟨by-definition⟩ - sin θ × sin φ + cos θ × cos φ =⟨ ℝ-+-comm ⟩ cos θ × cos φ + - sin θ × sin φ =⟨ ap (cos θ × cos φ +_) ℝ-neg-2 ⟩ cos θ × cos φ + - (sin θ × sin φ) =⟨ tri1 ⁻¹ ⟩ R (θ + φ) 𝟏 𝟏 ∎ addition : {θ φ : ℝ} (i j : Fin 2) → (R θ ⊗ R φ) i j = (R φ ⊗ R θ) i j addition {θ} {φ} i j = (R θ ⊗ R φ) i j =⟨ thm i j ⟩ R (θ + φ) i j =⟨ ap (λ x → R x i j) ℝ-+-comm ⟩ R (φ + θ) i j =⟨ thm i j ⁻¹ ⟩ (R φ ⊗ R θ) i j ∎
Streams and finite observations [ag-000D]
Streams and finite observations [ag-000D]
From Topology via logic
{-# OPTIONS --safe --without-K --guardedness --no-exact-split #-} module ag-000D where open import MLTT.Spartan open import MLTT.List
Stream can be defined as a coinductive record.
record Stream (A : 𝓤 ̇ ) : 𝓤 ̇ where coinductive constructor _∷_ field head : A tail : Stream A open Stream
For example a stream of all zero.
zeros : Stream 𝟚 head zeros = ₀ tail zeros = zeros
s ⊨starts o defines a relation that a stream can be
realized by a finite observation.
_⊨starts_ : Stream 𝟚 → List 𝟚 → 𝓤₀ ̇ s ⊨starts [] = ₀ = ₀ s ⊨starts (x ∷ xs) = (x = head s) × (tail s ⊨starts xs)
For example, the first bit zeros produces is
₀.
first-bit : zeros ⊨starts [ ₀ ] first-bit = refl , refl
Every stream can be realized by “no” observation.
realize-by-no-observation : (s : Stream 𝟚) → s ⊨starts [] realize-by-no-observation s = refl
We can define order relation for these finite observations.
_⊇_ : List 𝟚 → List 𝟚 → 𝓤₀ ̇ _ ⊇ [] = ₀ = ₀ [] ⊇ _ = 𝟘 (x ∷ l) ⊇ (x₁ ∷ l2) = (x = x₁) × (l ⊇ l2)
This order has antisymmetric
eq-condition : (l1 l2 : List 𝟚) → l1 ⊇ l2 → l2 ⊇ l1 → l1 = l2 eq-condition [] [] p q = refl eq-condition (x ∷ l1) (y ∷ l2) (ph , pt) (qh , qt) = x ∷ l1 =⟨ ap (_∷ l1) ph ⟩ y ∷ l1 =⟨ ap (y ∷_) (eq-condition l1 l2 pt qt) ⟩ y ∷ l2 ∎
, in fact total, which means a boring order. The order induces refinement of observations: if a observation is subsequence of another observation that realise the stream, then the stream also be realized by this subsequence.
refine-observation : {s : Stream 𝟚} → (l l2 : List 𝟚) → s ⊨starts l → l ⊇ l2 → s ⊨starts l2 refine-observation l2 [] _ _ = refl refine-observation (x ∷ l) (y ∷ l2) (x=head , tail) (x=y , rest) = (x=y ⁻¹ ∙ x=head) , refine-observation l l2 tail rest
Dependent equality in dependent type theory [ag-000C]
Dependent equality in dependent type theory [ag-000C]
這是從 https://mathstodon.xyz/@MartinEscardo/114751426538568913 學到的技巧。
{-# OPTIONS --safe --without-K #-} module ag-000C where open import Agda.Primitive renaming (Set to Type; Setω to Typeω) open import Agda.Builtin.Equality open import Agda.Builtin.Nat
假設我們有
- a type
X : Type - a family of types
A : X → Typeindexed byX
那我們常常會遇到有
x y : Xa : A xb : A yp : x = y
= 是 MLTT 的 identity type,p 是一個
x = y 的證明,這時候如果我們問 a = b
是沒有答案的,因為根據 MLTT,a 跟 b
的類型壓根兒就不一樣,這導致問題連寫都寫不下來,那怎麼辦?
方法是定義高階等式(又稱為 dependent equality 或是 PathOver 或是 path transport),在該依賴項等價的情況下把問題變成新的等式來讓 dependent type 語言表達等式
用案例來說就是如果有個 equality 是「類型不同」的(出於依賴項的不透明性,比如這裡 vector length 輸入的 associative 不同)
先定義一些下面案例會用到的輔助程式:
cong : {X Y : Type} (f : X → Y) {x₀ x₁ : X} → x₀ ≡ x₁ → f x₀ ≡ f x₁ cong {X} {Y} f refl = refl +-assoc : ∀ l m n → (l + m) + n ≡ l + (m + n) +-assoc zero m n = refl +-assoc (suc l) m n = cong suc (+-assoc l m n)
具體案例 vector ++ 的 associativity
data Vec (A : Type) : Nat → Type where [] : Vec A 0 _::_ : ∀{n} → A → Vec A n → Vec A (suc n) infixl 40 _::_ _++_ : {Y : Type} {l m : Nat} → (xs : Vec Y l) → (ys : Vec Y m) → Vec Y (l + m) [] ++ ys = ys (x :: xs) ++ ys = x :: (xs ++ ys) infixl 30 _++_
基於 x₀ ≡ x₁ 定義一個更高階的 equality
higher-equality : {X : Type} (A : X → Type) {x₀ x₁ : X} → A x₀ → x₀ ≡ x₁ → A x₁ → Type higher-equality A a₀ refl a₁ = a₀ ≡ a₁
但可以根據案例定義比較簡單的版本
_≡[_]_ : {X : Type} {x₀ x₁ : Nat} → Vec X x₀ → x₀ ≡ x₁ → Vec X x₁ → Type a₀ ≡[ refl ] a₁ = a₀ ≡ a₁
命題 (xs ++ ys) ++ zs ≡ xs ++ (ys ++ zs)
無法寫下,因為(meta-level 的)型別不同。 所以需要用高階等式描述
cong-cons : {X : Type} {m n : Nat} {xs : Vec X m} {ys : Vec X n} (x : X) (p : m ≡ n) → xs ≡[ p ] ys → x :: xs ≡[ cong suc p ] x :: ys cong-cons {X}{A} x refl refl = refl ++-assoc : {X : Type} (l m n : Nat) (xs : Vec X l) (ys : Vec X m) (zs : Vec X n) → (xs ++ ys) ++ zs ≡[ +-assoc l m n ] xs ++ (ys ++ zs) ++-assoc {X} zero m n [] ys zs = refl ++-assoc {X} (suc l) m n (x :: xs) ys zs = I where I : x :: (xs ++ ys) ++ zs ≡[ cong suc (+-assoc l m n) ] x :: (xs ++ (ys ++ zs)) I = cong-cons x (+-assoc l m n) (++-assoc l m n xs ys zs)
Second-Order Generalised Algebraic Theories: Signatures and First-Order Semantics [tt-000U]
Second-Order Generalised Algebraic Theories: Signatures and First-Order Semantics [tt-000U]
NOTE about Second-Order Generalised Algebraic Theories: Signatures and First-Order Semantics
這篇文章主要在探討程式語法的表示方式,並展示如何結合代數方法跟 HOAS。作者說他們跟隨 Uemura 把語言定義成 second-order generalised algebraic theories (SOGATs),通過一系列案例揭示 non-substructural languages 可以自然的定義成 SOGATs
- SOGAT 的形式定義 (using the syntax of a particular SOGAT)
- 定義兩種 SOGAT signatures 到 GAT signatures (signatures for quotient inductive-inductive types) 的轉換,分別基於同時替換(parallel substitution)與單一替換(single substitution)
按代數抽象程度區分 [local-0]
按代數抽象程度區分 [local-0]
從具體到抽象可以把語法表示看成
| 語法表示 | 能力 |
| abstract syntax trees (AST) | 把程式原文 parse 後直接儲存用的一系列資料結構 |
| well-scoped syntax tree | λx.x 跟 λy.y 在這類表示法裡面無法區分,也就是說綁定使用的具體名稱不再重要 |
| intrinsic well-typed terms | 這種表示把語法跟 typing relation 整合,所以 non well-typed 的程式甚至無法表達 |
| well-typed, quotiented by the conversion relation (GAT) | 加上更多 well-formness relation 的推廣代數理論,下面介紹 |
| SOGAT | GAT 推到 second-order,下面介紹 |
在 well-typed terms 上再加上 conversion relation 就變成廣義代數理論(generalised algebraic theory,簡稱 GAT),GAT 用來處理 dependently typed languages 時特別方便,因為 typing 依賴了 conversion relation。在 GAT 上只能定義保留了 conversion relation 的函數,因此連印出函數都無法定義,但 normalisation(正規化)、typechecking(型別檢查)跟 parametricity 這些函數保留 conversion 因此可定義。
對任何 GAT 來說,syntax 可以定義成 initial model,因此沒有區分語法跟語意的必要,某種意義上來說,一個程式語言就是一個 GAT。
HOAS 方法:按對 bindings/variables 的處理方式區分 [local-1]
HOAS 方法:按對 bindings/variables 的處理方式區分 [local-1]
HOAS 觀點關心 bindings 跟 variables 的處理方式,比如 De Bruijn indices 使名稱選擇與語意無關,但這也表示替換必須是語法的一部分,舉例來說 form of a category with families。
Logical frameworks 跟 higher-order abstract syntax (HOAS) 提供了另一種實現 bindings 跟 variables 的方式:使用 metatheory 的函數空間。
舉例來說,pure lambda calculus 的 lambda operation 的 type 是二階函數空間 (Tm → Tm) → Tm。這在理論上的解釋是 type-theoretic internal language of presheaves over the category of contexts and syntactic substitutions,在這個 topos 的 internal language 裡,lambda 的類型就長那樣。
Internal language 的觀點可以用來定義程式語言是什麼:有綁定的語言不是一個 GAT,而是一個二階的廣義代數理論(second-order generalised algebraic theory,簡稱 SOGAT),這種理論可以有二階操作(但不是任意高階)。
Untyped 或是 Simply typed 都有被定義成二階理論過,但 Uemura 是第一個用 SOGATs 定義有綁定的語言的人。這個理論真的很厲害,一個語言的 SOGAT 定義比 well-typed quotiented 定義還要抽象:SOGAT 連 contexts 跟 substitutions 都不用提到,這些會自動生成。但這不是一個 well-behaved 的代數理論,比如 second-order models 之間沒有有意義的 homomorphism。
為了描述 SOGAT 的一階模型、homomorphisms 或是 syntax 的 notion,作者把它轉成一個 GAT。這個過程中引入新的 sorts 給 contexts 跟 substitutions,然後把每個操作都用其 context index,second-order 的函數空間也由 context indexing 轉換成 first-order。因此得到一個有 some “correctness by construction” properties 的 GAT,比如每個操作都自動保留替換。這對複雜的理論來說,如果不是從 SOGAT 出發而是直接用其 GAT 表示,那這種屬性並不 trivial。
Cubical type theory 跟有 internal parametricity 的 type theory 都可以定義成 SOGATs,這些方法已經用來證明型別論的屬性。
Substructural (像是 linear or modal) type theories 無法用這篇論文說的方法用 SOGATs 定義,但有時候 presheaves over a substructural theory 提供的 substructural internal language 可以用來描述理論,像是 multi-modal type theory。
簡單的代數理論可以用 signatures 和方程式來表示,也可以 presentation independently 為 Lawvere theories。
GATs 的 syntactic signatures 可以用 preterms 跟 well-formedness relations 定義,也可以 presentation-independent 為 contextual categories 或 categories with families (CwFs) 或 clans。
GATs 的 theory of signatures (ToS) 方法落在 syntactic 跟 presentation-independent 方法中間:signatures 用某個 GAT 語法定義,這是一種設計來專用於定義簽名的類型理論。簽名跟我們在 Agda 裡寫下的 inductive datatype 定義一模一樣:A list (telescope) of the curried types of sorts and constructors。ToS 裡一個 signature 是一個理論的具體表示,但在 well-typed quotiented syntax 這層抽象上給出。這讓我們得到優雅的語意構造,又還是能用 signatures 工作。
SOGATs 同樣可以定義成 syntactically 或 presentation-independently(用 representable map categories 或是 CwFs with locally representable types)
這篇論文貢獻了 ToS 風格的 SOGATs 定義。SOGAT signatures 的理論本身也是 SOGAT,所以這個理論可以描述自己。
避免了循環論證,因為我們首先將 SOGAT 簽名定義為 GAT,從而引導 SOGAT 簽名理論,而 GAT 簽名理論(即 GAT 的語法)本身可以使用 Church 編碼進行引導。
Contributions [local-2]
Contributions [local-2]
The main takeaway of this paper is that structural languages are SOGATs.
We justify this claim through several examples. Our technical contributions are the following:
- The theory of SOGAT signatures (ToS+), a domain-specific type theory in which every closed type is a SOGAT signature. As it is a structural type theory, it can be defined as a SOGAT itself. Signatures can be formalised in ToS+ without encoding overhead.
- A translation from SOGAT signatures to GAT signatures based on a parallel substitution calculus. Thus, for every SOGAT, we obtain all of the semantics of GATs: a category of models with an initial object, (co)free models, notions of displayed models and sections, the fact that induction is equivalent to initiality, and so on. The GAT descriptions that we obtain are readable, do not contain occurrences of Yoneda as in usual presheaf function spaces. Correctness of the translation is showed by proving that internally to presheaves over a model of the GAT, a second-order model of the SOGAT is available.
- We define an alternative translation producing a single substitution calculus.
作者開始展示如何把各種 logic 或程式語言定義成代數理論。這邊我寫下每個代數理論的 agda 版本
Schönfinkel's combinator calculus (Algebraic Theories) [ag-0003]
Schönfinkel's combinator calculus (Algebraic Theories) [ag-0003]
{-# OPTIONS --safe --without-K #-} module ag-0003 where open import MLTT.Spartan
Combinator calculus 可以看成一個代數理論,這時候它有
- 一個 sort of terms
- 一個 binary
- 兩個 nullary operations
- 兩個等式
record combinator-calculus : 𝓤₁ ̇ where field Tm : 𝓤₀ ̇ _·_ : Tm → Tm → Tm K : Tm S : Tm Kβ : {u f : Tm} → K · u · f = u Sβ : {f g u : Tm} → S · f · g · u = f · u · (g · u) infixl 30 _·_
- 從這個符號可以明顯看出代數/模型的概念
- Combinator calculus 的 quotiented syntax 是初始模型,它總是存在。
- Notions of homomorphism, displayed/dependent model, induction, products and coproducts of models, free models, and so on, are derivable from the signature, as described in any book on universal algebra
- Algebraic Theory 的 initial algebra 叫做 quotient inductive type
其他 single-sorted algebraic theories 著名案例:
- 邏輯:經典(或直覺主義)命題邏輯,定義為布林代數(或海廷代數)理論
- 代數:monoids、群、環、lattices 等等
Generalised algebraic theories (GATs) [local-3]
Generalised algebraic theories (GATs) [local-3]
Generalised algebraic theories (GATs) 的 sort 可以 indexed by 其他 sort。案例有 typed combinator calculus、propositional logic with Hilbert-style proof theory、theories of graphs、preorders、categories 等等
Typed combinator calculus (Generalised algebraic theories) [ag-0004]
Typed combinator calculus (Generalised algebraic theories) [ag-0004]
{-# OPTIONS --safe --without-K #-} module ag-0004 where open import MLTT.Spartan
record typed-combinator-calculus : 𝓤₁ ̇ where field
給 types 的 sort
Ty : 𝓤₀ ̇
每個 type 對應(index)一個 term 用的 sort
Tm : Ty → 𝓤₀ ̇ ι : Ty _⇒_ : Ty → Ty → Ty _·_ : {A B : Ty} → Tm (A ⇒ B) → Tm A → Tm B K : {A B : Ty} → Tm (A ⇒ B ⇒ A) S : {A B C : Ty} → Tm ((A ⇒ B ⇒ C) ⇒ (A ⇒ B) ⇒ A ⇒ C) Kβ : {A B : Ty} {u : Tm A} {f : Tm B} → K · u · f = u Sβ : {A B C : Ty} {f : Tm (A ⇒ B ⇒ C)} {g : Tm (A ⇒ B)} {u : Tm A} → S · f · g · u = f · u · (g · u) infixl 40 _·_ infixr 30 _⇒_
上述 Algebraic Theory 的通用代數特徵可以推廣到 GAT。具體來說,每個 GAT 都具有由 quotient inductive-inductive type 給出的語法,我們有 free 模型和 cofree 模型。
Second-order algebraic theories (SOATs) [local-4]
Second-order algebraic theories (SOATs) [local-4]
如果一個語言有變數或是綁定,就被定義成一個二階理論。
Lambda calculus (Second-order algebraic theories) [ag-0005]
Lambda calculus (Second-order algebraic theories) [ag-0005]
{-# OPTIONS --safe --without-K #-} module ag-0005 where open import MLTT.Spartan
record lambda-calculus : 𝓤₁ ̇ where field Tm : 𝓤₀ ̇
lam 的(metatheory)型別不是一階的(not strictly
positive)
lam : (Tm → Tm) → Tm _·_ : Tm → Tm → Tm β : {f : Tm → Tm} {u : Tm} → lam f · u = f u infixl 30 _·_
By the syntax of lambda calculus, we mean the syntax for the GAT of Definition 4. However, we still prefer to define lambda calculus as a SOGAT: it is a shorter definition, does not include boilerplate, and ensures that once translated to its first-order version, all operations respect substitution by construction.
此外,我們可以像邏輯框架一樣,使用二階表示來進行程式設計。這意味著,使用二階表示,我們可以定義 derivable operation 並證明 derivable 等式,而不是像證明 admissible 那樣需要歸納法。
舉例來說 Y combinator 是 derivable operation。可以證明它是 fixpoint combinator:
Y : Tm Y = lam (λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) Y-is-fixed-point : {f : Tm} → Y · f = f · (Y · f) Y-is-fixed-point {f} = Y · f =⟨by-definition⟩ lam (λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) · f =⟨ β ⟩ (λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) f =⟨ refl ⟩ (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x))) =⟨ β ⟩ f · ((lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) =⟨ refl ⟩ f · ((λ f → (lam (λ x → f · (x · x))) · (lam (λ x → f · (x · x)))) f) =⟨ ap (f ·_) (β ⁻¹) ⟩ f · (Y · f) ∎
這種推理對任何 second-order model 都有效,而且任何 first-order model 都可以在 internal language of presheaves over first-order model 裡被升級成 second-order model。
但注意沒有可用的 SOAT models 和 之間的同態概念。為了討論同態或語法,我們將 SOAT 轉換為一階 GAT:加上上下文、替換、索引 Tm 以及所有基於上下文的操作,然後 lam 就變成了一個以擴展上下文中的項作為輸入的一階函數。轉換出來的 GAT 就是
Lambda calculus (GAT) [ag-0006]
Lambda calculus (GAT) [ag-0006]
{-# OPTIONS --safe --without-K #-} module ag-0006 where open import MLTT.Spartan hiding (_∘_; id)
作者這邊開始解釋從二階理論得出一階理論(GAT)的標準過程
record first-order-lambda-calculus : 𝓤₁ ̇ where field Con : 𝓤₀ ̇ Sub : Con → Con → 𝓤₀ ̇
有 terminal object 的 category
_∘_ : {Δ Γ Θ : Con} → Sub Δ Γ → Sub Θ Δ → Sub Θ Γ assoc : {A B C D : Con} {γ : Sub C D} {δ : Sub B C} {θ : Sub A B} → (γ ∘ δ) ∘ θ = γ ∘ (δ ∘ θ) id : {Γ : Con} → Sub Γ Γ id-left : {A B : Con} {γ : Sub A B} → id ∘ γ = γ id-right : {A B : Con} {γ : Sub A B} → γ ∘ id = γ -- empty context: zero ◇ : Con ε : {Γ : Con} → Sub Γ ◇ -- terminal ◇η : {Γ : Con} → (σ : Sub Γ ◇) → σ = ε
sort Tm 現在 indexed by Con 且有一個
instantiation operation,這個 operation 是 functorial
([◦], [id]).
Tm : Con → 𝓤₀ ̇ _[_] : {Γ Δ : Con} → Tm Γ → Sub Δ Γ → Tm Δ [id] : {Γ : Con} {t : Tm Γ} → t [ id ] = t [∘] : {Θ Γ Δ : Con} {t : Tm Γ} {γ : Sub Δ Γ} {δ : Sub Θ Δ} → t [ γ ∘ δ ] = t [ γ ] [ δ ]
context extension 讓 contexts 是 natural number algebra
_▹ : Con → Con
substitutions 是一串 terms,由組成元件表達
_,,_ : {Δ Γ : Con} → Sub Δ Γ → Tm Δ → Sub Δ (Γ ▹)
有了 contexts 跟 substitutions,變數就可以定義成 De Bruijn indices:
0 = q1 = q[p]2 = q[p] [p],以此類推
p : {Γ : Con} → Sub (Γ ▹) Γ q : {Γ : Con} → Tm (Γ ▹)
應該滿足的等式規則
▹β₁ : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm Δ} → p ∘ (γ ,, t) = γ ▹β₂ : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm Δ} → q [ γ ,, t ] = t ▹η : {Δ Γ : Con} {σ : Sub Δ (Γ ▹)} → σ = (p ∘ σ ,, q [ σ ]) lam : {Γ : Con} → Tm (Γ ▹) → Tm Γ lam[] : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm (Γ ▹)} → (lam t)[ γ ] = lam (t [ γ ∘ p ,, q ]) _·_ : {Γ : Con} → Tm Γ → Tm Γ → Tm Γ ·[] : {Δ Γ : Con} {γ : Sub Δ Γ} {t u : Tm Γ} → (t · u)[ γ ] = t [ γ ] · (u [ γ ]) β : {Δ Γ : Con} {γ : Sub Δ Γ} {t : Tm (Γ ▹)} {u : Tm Γ} → lam t · u = t [ id ,, u ] infixl 40 _∘_ infixl 30 _,,_ infixl 40 _·_ infixl 50 _[_]
Second-order generalised algebraic theories (SOGATs) [local-5]
Second-order generalised algebraic theories (SOGATs) [local-5]
SOGATs combine the two previous classes: sorts can be indexed over previous sorts and second-order operations are allowed.
Simply typed lambda calculus [ag-0007]
Simply typed lambda calculus [ag-0007]
{-# OPTIONS --safe --without-K #-} module ag-0007 where open import MLTT.Spartan open import UF.Equiv
record simply-typed-lambda-calculus : 𝓤₁ ̇ where field Ty : 𝓤₀ ̇ _⇒_ : Ty → Ty → Ty
generalised 的部分是因為 index Tm by Ty
Tm : Ty → 𝓤₀ ̇
綁定的部分
lam : {A B : Ty} → (Tm A → Tm B) → Tm (A ⇒ B) _·_ : {A B : Ty} → Tm (A ⇒ B) → (Tm A → Tm B) stlc-cong : {A B : Ty} → Tm (A ⇒ B) ≃ (Tm A → Tm B)
一樣參照 first-order lambda calculus 的過程,加上 contexts、加上 substitutions,相應的 first-order 等式跟改寫,就會得到 simply-typed-lambda-calculus 的 GAT。
Minimal intuitionistic first-order logic (SOGAT) [ag-0008]
Minimal intuitionistic first-order logic (SOGAT) [ag-0008]
{-# OPTIONS --safe --without-K #-} module ag-0008 where open import MLTT.Spartan open import UF.Subsingletons
record minimal-intuitionistic-first-order-logic : 𝓤₁ ̇ where field For : 𝓤₀ ̇ Tm : 𝓤₀ ̇ _⊃_ : For → For → For All : (Tm → For) → For Eq : Tm → Tm → For Pf : For → 𝓤₀ ̇ Pf-is-prop : (A : For) → is-prop (Pf A) intro⊃ : {A B : For} → (Pf A → Pf B) → Pf (A ⊃ B) elim⊃ : {A B : For} → Pf (A ⊃ B) → (Pf A → Pf B) intro∀ : {A : Tm → For} → ((𝑡 : Tm) → Pf (A 𝑡)) → Pf (All A) elim∀ : {A : Tm → For} → Pf (All A) → ((𝑡 : Tm) → Pf (A 𝑡)) introEq : {t : Tm} → Pf (Eq t t) elimEq : {t t' : Tm} → (A : Tm → For) → Pf (Eq t t') → Pf (A t) → Pf (A t')
一樣參照 first-order lambda calculus 的過程,加上 contexts、加上 substitutions,相應的 first-order 等式跟改寫。
Polymorphic lambda calculus (SOGAT) [ag-0009]
Polymorphic lambda calculus (SOGAT) [ag-0009]
{-# OPTIONS --safe --without-K #-} module ag-0009 where open import MLTT.Spartan
record polymorphic-lambda-calculus : 𝓤₁ ̇ where field Ty : 𝓤₀ ̇ Tm : Ty → 𝓤₀ ̇ _⇒_ : Ty → Ty → Ty lam : {𝐴 𝐵 : Ty} → (Tm 𝐴 → Tm 𝐵) → Tm (𝐴 ⇒ 𝐵) _·_ : {𝐴 𝐵 : Ty} → Tm (𝐴 ⇒ 𝐵) → (Tm 𝐴 → Tm 𝐵) All : (Ty → Ty) → Ty Lam : {𝐴 : Ty → Ty} → ((𝑋 : Ty) → Tm (𝐴 𝑋)) → Tm (All 𝐴) _•_ : {𝐴 : Ty → Ty} → Tm (All 𝐴) → ((𝑋 : Ty) → Tm (𝐴 𝑋))
一樣參照 first-order lambda calculus 的過程,加上 contexts、加上 substitutions,相應的 first-order 等式跟改寫。
System Fω (SOGAT) [ag-000A]
System Fω (SOGAT) [ag-000A]
{-# OPTIONS --safe --without-K #-} module ag-000A where open import MLTT.Spartan
record system-F-ω : 𝓤₁ ̇ where field □ : 𝓤₀ ̇ Ty : □ → 𝓤₀ ̇ _⇛_ : □ → □ → □ LAM : {K L : □} → (Ty K → Ty L) → Ty (K ⇛ L) _●_ : {K L : □} → Ty (K ⇛ L) → (Ty K → Ty L) ∗ : □ Tm : Ty ∗ → 𝓤₀ ̇ All : {K : □} → (Ty K → Ty ∗) → Ty ∗ Lam : {K : □}{A : Ty K → Ty ∗} → ((X : Ty K) → Tm (A X)) → Tm (All A) _•_ : {K : □}{A : Ty K → Ty ∗} → Tm (All A) → ((X : Ty K) → Tm (A X)) _⇒_ : Ty ∗ → Ty ∗ → Ty ∗ lam : {A B : Ty ∗} → (Tm A → Tm B) → Tm (A ⇒ B) _·_ : {A B : Ty ∗} → Tm (A ⇒ B) → (Tm A → Tm B)
System Fω 轉換後有
- 3 個 operations 綁定 Ty-variables
- 1 個 operation 綁定 term-variable
Minimal Martin-Löf type theory (SOGAT) [ag-000B]
Minimal Martin-Löf type theory (SOGAT) [ag-000B]
{-# OPTIONS --safe --without-K #-} module ag-000B where open import MLTT.Spartan open import MLTT.NaturalNumbers
variable 𝑖 : ℕ record minimal-martin-lof-type-theory : 𝓤₁ ̇ where field Ty : ℕ → 𝓤₀ ̇ U : (𝑖 : ℕ) → Ty (succ 𝑖) Tm : Ty 𝑖 → 𝓤₀ ̇ c : Ty 𝑖 → Tm (U 𝑖) El : Tm (U 𝑖) → Ty 𝑖 PI : (A : Ty 𝑖) → (Tm A → Ty 𝑖) → Ty 𝑖 Lift : Ty 𝑖 → Ty (succ 𝑖) lam : {𝐴 : Ty 𝑖}{𝐵 : Tm 𝐴 → Ty 𝑖} → ((𝑎 : Tm 𝐴) → Tm (𝐵 𝑎)) → Tm (PI 𝐴 𝐵) _·_ : {𝐴 : Ty 𝑖}{𝐵 : Tm 𝐴 → Ty 𝑖} → Tm (PI 𝐴 𝐵) → ((𝑎 : Tm 𝐴) → Tm (𝐵 𝑎)) mk : {𝐴 : Ty 𝑖} → Tm 𝐴 → Tm (Lift 𝐴) un : {𝐴 : Ty 𝑖} → Tm (Lift 𝐴) → Tm 𝐴
這個理論的對應 GAT
得到一個具有族的範疇(CwF),更準確地說,是一個具有 N 個 families
的範疇,這些族配備了 familywise Π-types、宇宙以及族之間的一步向上提升。
這些類型是 Ty : Con → N → Set 和
Tm : (Γ : Con) → Ty Γ 𝑖 → Set,其中 𝑖
論證隱含在後者中。
後面幾節
- 第三節 Theories of signatures as SOGATs,開始把 signatures 理論也寫成 SOGAT 來討論
- 第四節 Naive semantics of SOGAT signatures,討論 for any SOGAT signature 的 a notion of first-order model.
- 第五節 Direct semantics of SOGAT signatures,用一個更小心版本的 presheaf model 定義 first-order models of SOGATs
- 第六節 GAT signature semantics of SOGAT signatures,把 SOGAT signatures 轉成 GAT signatures 的方法
Intrinsically typed term [ag-0002]
Intrinsically typed term [ag-0002]
{-# OPTIONS --safe --without-K #-} module ag-0002 where open import MLTT.Spartan hiding (Type) open import MLTT.List
Type 在 STLC 還只需要是一個簡單的 formation
data Type : 𝓤₀ ̇ where bool : Type _⇒_ : Type → Type → Type infixr 50 _⇒_ variable S T : Type
Context 通常會自訂,比如 MLTT 需要兩種綁定時自訂就會更方便一些
Ctx = List Type _▷_ : Ctx → Type → Ctx Γ ▷ T = T ∷ Γ infix 40 _▷_ variable Γ : Ctx
Intrinsically-scoped de Brujin indices
基本上變數都長這樣
data _∋_ : Ctx → Type → 𝓤₀ ̇ where here : Γ ▷ T ∋ T there : Γ ∋ T → Γ ▷ S ∋ T infix 20 _∋_ variable x : Γ ∋ T
Intrinsically-typed terms
確保 term 是類型良好的一種方式就是從一開始就跟 context 一起構造,讓 terms 必須是 well-typed
data _⊢_ : Ctx → Type → 𝓤₀ ̇ where true false : Γ ⊢ bool var : Γ ∋ T → Γ ⊢ T lam : Γ ▷ S ⊢ T → Γ ⊢ S ⇒ T _·_ : Γ ⊢ S ⇒ T → Γ ⊢ S → Γ ⊢ T if_then_else_ : Γ ⊢ bool → Γ ⊢ T → Γ ⊢ T → Γ ⊢ T infix 30 _⊢_
Video. Why You Can't Bring Checkerboards to Math Exams [math-001E]
Video. Why You Can't Bring Checkerboards to Math Exams [math-001E]
A cool way to do multiply, divide and root!
Definition. Diffeological space [math-001D]
Definition. Diffeological space [math-001D]
A diffeological space is a pair consists of a given set and a diffeology consists of a collection of parameterizations satisfying the following conditions:
- All parameterizations with domain belong to , namely all the points of
- If is a parameterization, and is a smooth map between cartesian spaces, then belongs to
- If is a parameterization, an open cover of that each restriction , then
If is a diffeology, then we call a parameterization that belongs to it a plot.
Lemma. Presheaves are colimits of representables [math-001B]
Lemma. Presheaves are colimits of representables [math-001B]
The presheaf is the colimit of the functor ,
where is the yoneda embedding, is the category of elements of . For morphism .
Proof. [local-0]
Proof. [local-0]
We first show that is a cocone, for each object , there is a morphism
here abuse notation that has a corresponding in because the Yoneda lemma.
and for each , the following diagram commutes
hence is a cocone. Given any other cocone , which means a collection of sections
where for each by definition. The point is if we define a natural transformation
naturality follows because implies . It is clear that is the unique natural transformation under , showing that is the colimit.
Presheaves, Yoneda embedding, and Yoneda lemma [math-001A]
Presheaves, Yoneda embedding, and Yoneda lemma [math-001A]
Definition. Presheaf [local-0]
Definition. Presheaf [local-0]
Let be a category. A presheaf over is a functor of the form
For each object , we will denote by
the evaluation of at . The set will sometimes be called the fibre of the presheaf at , and the elements of thus deserve the name of sections of over .
For morphism , the induced map from denotes .
The category of presheaves over denotes .
Definition. Yoneda embedding [local-1]
Definition. Yoneda embedding [local-1]
Yoneda embedding is a functor
we denote
Lemma. Yoneda [local-3]
Lemma. Yoneda [local-3]
For any presheaf over , there is a natural bijection of the form
Proof. [local-2]
Proof. [local-2]
We first define inverse map , given a section of over , i.e. , we have
for each morphism . This indeed defines a morphism in .
Now check and indeed are inverse of each other. First: given , we have
Another direction: given , we have
for each . Naturality is obvious, hence they form a natural bijection.
隱式編程:coherence 與 stability 屬性 [tt-000T]
隱式編程:coherence 與 stability 屬性 [tt-000T]
這篇是 COCHIS: Stable and coherent implicits 的筆記
隱式編程機制是指,使用型別指導的推導能力,在使用者不提供完整資訊的情況下給出程式語意的技術。比如 Haskell 的 type class、Rust 的 trait 等。合成的過程叫做 resolution。
Haskell 的 type class 的一個重要特徵是給定的類型只會有一個 instance 符合。coherence 在這個意義下指的是,給出的程式語意是唯一的,也就是說對某段合法程式碼,不會合成出超過一個語意。
比如説 Haskell 會拒絕 show (read "3") == "3" 這段程式碼,因為根據 type class resolution 有很多種可能性(show : α -> String 跟 read : String -> α)
- 選了
α := Float那結果是False,因為show (read "3") == "3.0" - 選了
α := Int那結果是True - 選了
α := Char那結果是True
所以這種會導致有多種語意出現的程式就需要被拒絕。
Haskell 的 overlapping instances 技術是對上述問題的一種推廣(使我們可以接受更多程式),比如說
class Trans α where trans :: α → α instance Trans α where trans x = x instance Trans Int where trans x = x + 1
對於程式 trans 3 應該要決定出什麼結果?Overlapping 的決定是,因為 α := Int 比沒有決定更特定,因此選 instance Trans Int。然而,也有 overlapping 策略也無法決定的情況,比如下面比較刻意的
class C α β where m :: α → β → Bool instance C Bool α where mx y = x instance C α Bool where mx y = y
對程式 m True False 兩個 instances 都一樣特定,沒辦法決定,因此這段程式碼也必須被拒絕。
Stability 是跟 coherence 高度相關的屬性。不正式的說,stable 是指 type variables 的實例化與否不影響 resolution 的結果。但 overlapping 技術會影響這個結果,比如
bad :: α → α bad x = trans x
就是一個 unstable 的定義。如果寫成 Trans α => α → α 就不一樣了,這表示 α 交由呼叫 bad 的地方決定,但這裡則是必須在定義處馬上決定,如果 Haskell 接受這段定義,那可能會選擇第一個 instance Trans,導致 bad 3 是 3 而 trans 3 是 4。雖然 bad x := trans x 是定義等價。
也可以參考 https://blog.ezyang.com/2014/07/type-classes-confluence-coherence-global-uniqueness/ 的案例跟論點。
Definition. 流形上的微分式 [math-0019]
Definition. 流形上的微分式 [math-0019]
設 為 differentiable manifold 的局部座標,可以把微分式定義為 的對偶基底,記為 。亦即
一階微分式的整體記為 。
任何給定的微分式 可以寫成向量形式
對一個 ,什麼是 ?用向量微積分的觀點,是函數 的一階變化量
因此其類型是 的線性函數,通過空間對偶可知這就是 的元素。
性質一
證明如下:設
又有
因此
然而要注意到,並不是每個 都可以表示成某個 的微分 。
性質二
而且,對於每個具體的 , 顯然是一種 的特例,因此也可以定義
驗證
可見如此定義的 跟取對偶基底的結果相同。
Definition. 切向量場沿曲線平行 (parallel) [math-0018]
Definition. 切向量場沿曲線平行 (parallel) [math-0018]
令 為一 -affine manifold 上一 -曲線。 為 上有意義的切向量場(i.e. 對所有 ,可以對 可微的指定一個 )
稱 沿 為平行。
若適當的局部座標為 ,則
令 (即速度向量),則
因此
因此
沿 平行的充要條件為滿足一階線性方程組
測地線方程組推導 [math-0017]
測地線方程組推導 [math-0017]
令 為一 -affine manifold 上一 -曲線,我們定義當
對所有 成立時, 為一測地線。只要參考切向量場沿著某一曲線如何被視為平行定義的推廣就可以直觀的看出測地線的幾何意義。
藉由座標 ,可將 表達為
故推導當 為一測地線時,有方程式
因此測地線方程組就是指
The Basel problem with trigonometric Fourier series [math-0016]
The Basel problem with trigonometric Fourier series [math-0016]
An idea is define on . Its trigonometric Fourier series was:
which is periodic and converges to in .
Observing that is even, hence
for all . Now compute
and each is
Now let's focus on integral by part
and again
It seems complicated, but in fact we have , hence we can ignore them in this definite integral
Therefore, if we compute can get
Hence
Definition. Impredicative [tt-000V]
Definition. Impredicative [tt-000V]
參考 https://github.com/AndrasKovacs/elaboration-zoo/tree/master/06-first-class-poly
In type theory
A universe is impredicative if function types whose codomains are in the universe are always in the universe, regardless of their domain types.
如果 可以通過檢查,這個 Universe 就是 impredicative 的,有 impredicative universe 存在的類型理論就叫做有 impredicativity。像 Rocq 或是 Lean 都有特殊的 Prop universe 有這樣的特性。
In Elaboration algorithm
An elaboration algorithm is impredicative if it is able to solve metavariables to implicit function types.
is diffeomorphic to [math-0015]
is diffeomorphic to [math-0015]
Construction
- and
- and
and use
- and
- and
The diffeomorphism defined as
Given we have a ratio , we want to recover a point on , how to get this inverse map? The idea is
Now we can use quadratic formula to solve (and remind that ):
However, hence
By this we can see
Therefore, is
The similiar reasoning can show
Hence, for (i.e. ) we have
By component, first check :
Then check :
So is indeed well defined, and smooth on it domain, the inverse defined as
where and because the equivalence. These maps are smooth on and agree each other (inverse the ratio because the position) when meet hence well defined. Hence is a diffeomorphism.
Proposition. is open [math-4M36]
Proposition. is open [math-4M36]
Let the set of those lines that intersect .
Proof. [local-0]
Proof. [local-0]
By definition, is open if and only if its preimage in is open (its preimage under the map ).
Hence, we want to prove is open in . Because , and inherits the topology of , so if we can show an open set such that , then is an open set. Then we can see if we define , it's open and , so is open in and is open in .
Definition. Real Projective -space as quotient of [math-UGKQ]
Definition. Real Projective -space as quotient of [math-UGKQ]
Another famous view is viewing as the quotient of the sphere , because it’s obvious that each element (a line) of projective -space intersects exactly two points, and the two points are antipodal points!
Use to represent an element of that intersects at .
Therefore, if we make a quotient relation:
Then we can see that , this homeomorphism can be used to transfer the -structure on to .
Definition. Jacobian matrix [math-0014]
Definition. Jacobian matrix [math-0014]
Let be a map, hence we can view each component is a function :
with respect to standard bases, and , is given by the matrix of partial derivatives (the Jacobian matrix) in the following sense
Or using the index notation, so can be expressed as:
Type system 的 Soundness 與 Completeness [tt-000S]
Type system 的 Soundness 與 Completeness [tt-000S]
我們說型別系統 sound 的時候,意思是如果一隻程式的型別不正確,系統就不會接受這隻程式。這蘊含了如果程式被系統接受 (type-checked),那就一定是沒有類型錯誤的程式。
我們說型別系統 complete 的時候,意思是如果一隻程式的型別正確,就一定會被系統接受。
我們通常更偏好滿足 soundness,因為有型別錯誤卻被接受的程式,因為比起有幾個需要改寫幾隻程式的麻煩,unsound 往往能造成更大的問題。
Definition. Predicative [tt-000R]
Definition. Predicative [tt-000R]
Counterexamples in Type Systems
A type system is predicative if definitions can never be referred to, even indirectly, before they are defined.
Definition. Injectivity [tt-000Q]
Definition. Injectivity [tt-000Q]
Counterexamples in Type Systems
如果我們說一個型別建構子 是 Injective,那麼意思是如果 則 。
一個程式語言的各個參數化型別不必然都具有這個特性。
代數幾何:非常基本的部分 [math-XGSJ]
代數幾何:非常基本的部分 [math-XGSJ]
代數幾何的核心物件是:多個多項式等式構成的系統
- 有 個變數,記為
- 有 個多項式
幾何上我們就是研究 中解集的軌跡。代數上我們就是研究
這個 algebra。事實上任何有限生成 ring 都可以表示成這個形式: finitely generated 表示存在一個 surjective map ,然後 Hilbert Basis theorem 說明這個 map 的 kernel 可以用有限個元素生成。
這個理想是由 linear combinations 的形式組成的,其中 是多項式
Definition. maximal ideal [math-0013]
Definition. maximal ideal [math-0013]
A maximal ideal of a commutative ring is a proper ideal of such that, whenever is an ideal of and , then or .
An equivalent condition is is a field if and only if is maximal.
Definition. prime ideal [math-0012]
Definition. prime ideal [math-0012]
Let be a ring and be an ideal, the followings are equivalent conditions to say that is prime
- is prime if than or for all
- is prime if is an integral domain
Proof
Backward
Let be an integral domain, that's say if and , then or . Let be the zero element of (i.e. ), then . Hence or , implies or .
Forward
Let be a prime ideal, let
then and therefore, or . Hence or is the zero coset in .
Algorithm. 君主選舉 [cs-000I]
Algorithm. 君主選舉 [cs-000I]
前提
- 每個節點入場的時候都分配到一個代數(generation),這個數字是唯一的
- 第一個啟動節點直接當選
當原始的領導者掛了(一段時間無回應),注意到這點的節點就開始問比自己老的所有節點是不是還活著
- 收到 alive 回應,或是得到其他更高優先順序的候選節點資訊。
- 從中選出最老(代數數字最小)的節點告知它當選了,當選節點會廣播自己當選的消息。
問題
- 注意到領導者無回應而發起投票的節點可以超過一個
- 兩個發起投票的節點有連線的節點當然可能不同
比如 5 6 都注意到 1 死亡,發起投票。3 4 跟 5 有連線於是選出 2;2 3 跟 6 有連線於是選出 3。這時候 2 3 就都覺得自己是領導者了,而且 5 對 6 的通知還是更不正確的結果。
當然補上當選節點廣播之後,較年輕的當選者會自己去除這個屬性也是可以,但這中間會有一小段時間可能發生(以資料庫而言)雙重寫入而遺失資料。
而且要注意到實際上當然可以比這麻煩的多,比如通訊密集時,更容易讓 leader 過載;同時 90% 的節點都發現這點並發起投票,那麼消除腦分裂前的混亂就會特別嚴重。
Internal language 之用 [math-0011]
Internal language 之用 [math-0011]
這是 An informal introduction to topos theory 的閱讀筆記,Leinster 在這裡說 generalized elements 可以說是 Category 的 internal language。而 set theoretic 裡面使用 element 的論證多半都能改用這樣的語言進行,甚至,不使用 LEM 與 AC 的構造式證明,可以在任意 topos 中使用。
除了在 Generalized element 已經討論過的 product ,topos 還有 exponentials ,equalizer 也可以記為
表示 。
這樣就無需使用大量的 diagram,而是採用數學家已經熟悉的集合式的論證即可。
Definition. Generalized element [math-0010]
Definition. Generalized element [math-0010]
Let be a category, and let be an object of . A generalized element of is simply a map in with codomain .
A generalized element is shape or -element of .
When (the terminal) then -elements are called global elements.
Global elements can be very boring, for example in the category of groups.
The language of generalized elements is the internal language of the category. For example, let be a category with finite products. An -element of consists of two component and is denoted by , hence extended the notation of set-theoretic Cartesian product of global elements.
Definition. Immersion, embedding, and submanifold [math-000Z]
Definition. Immersion, embedding, and submanifold [math-000Z]
Let be differentiable manifolds (dimensions are and respectively). A differentiable map is said to be an immersion if
is injective for all .
If in addition, is a homeomorphism onto , where has the subspace topology induced from , then is an embedding.
If and the inclusion is an embedding, then is a submanifold of .
Proposition. Right adjoint fully faithful <=> counit is isomorphism [math-000Y]
Proposition. Right adjoint fully faithful <=> counit is isomorphism [math-000Y]
Suppose is an adjunction, and is fully faithful, then counit is an isomorphism
Proof
Forward direction
To prove counit is an isomorphism, we need to find an inverse and show pre and post composition of them are identity. Let , then we have two targets
-
Apply to get
hence the target is , right triangle fills the target.
-
Use counit naturality on to get
Therefore, we have target , left triangle fills the target.
Backward direction
For is faithful, we want to know if then . We first obtain two equations via naturality of counit:
Replace with then we have , counit is an isomorphism and hence left-cancellable, .
For is full, we want to show every there is a such that . Let (where is the hom-set equivalence of adjunction), this is same as asking
because isomorphism property, we have
now we use isomorphism to cancel right, so .
Counterexample. no need to be identity when [math-000X]
Counterexample. no need to be identity when [math-000X]
The counterexample in the category of sets is
We have for all , but is not identity. Where represent the set with and elements, respectively.
tr-notes transclude 的發展 [tr-0007]
tr-notes transclude 的發展 [tr-0007]
tr 最開始我的想法是讓每一張卡片自己都輸出一個 HTML 網頁,然後就想到「哎糟糕,被嵌入 (transclude 概念) 的網頁會有重複的共用元素」就放棄了,當時認為所以必須像 forester 那樣用 XML 才行
好久以後我再次考慮(2025/05)實現一個 forester fork 時才想到,只要每張卡生成一個 a.index.html 一個 a.embed.html 就可以避免重複元素了
順著這個想法我用 iframe 嵌入來實現功能,直到我實在解不開 JS 的工作空間問題,這逼我思考其他方案。結果過了幾天我想到其實根本不用這麼麻煩xd,transclude 直接讀 embed 的內容就好了(並且 escape 排版確保不破壞 pre tag 等對排版敏感的內容)
現在剩下的問題就是其實 index 其實也沒必要再用 racket 生成一次,而是應該把 header, footer 等內容插入,讀取自己的 embed 檔案,但目前耦合比較多(依靠 generate-index? 判斷是否生成這些區塊),需要重新思考怎麼編排這些程式
魔物獵人荒野 充能斧 操作筆記 [game-0000]
魔物獵人荒野 充能斧 操作筆記 [game-0000]
基本操作
- △: 劍 牽制斬
- △ + O: 劍 突進斬
- O 長按: 劍 蓄力上撈斬
- R2 + △: 劍 變形斬
- R2 + O: 劍 充能
強化瓶系統
最有效率的集氣連技是: O 長按 → △
但魔物太靈活時這樣可能會一直落空,不一定要堅持這樣打
充能模式
1. 充能盾牌(紅盾)
架盾操作:- R2 + O 之後保持 O 不放開
- △ + O 三次接 R2
- 突進斬
- 盾突刺
- 高解
- 屬性強化迴旋斬
2. 充能劍(紅劍)
操作流程:- R2 + O 後按住 △ 進行蓄力
- 放開後打出「劍:高壓屬性斬」
3. 充能斧(紅斧)
觸發條件有三種(任何一個達成就會觸發紅斧模式):- L2 瞄準用 R1 集中攻擊打到傷口(必須命中才會觸發)
- 精準防禦之後按 △
- 騎乘打出處決後觸發
出紅斧是為了能長按攻擊鍵 △ 或是 O 時,斧會持續輸出而不是只有一次輸出
Proposition. Christoffel 等於 0 iff g 是常數(平直空間) [math-GDOS]
Proposition. Christoffel 等於 0 iff g 是常數(平直空間) [math-GDOS]
Christoffel 定義為
Proof. [local-0]
Proof. [local-0]
(<=) 是常數表示微分為 ,因此 Christoffel
(=>) 因為
對兩邊取積分可知
Naturality cannot be given by a family of isomorphisms [math-000S]
Naturality cannot be given by a family of isomorphisms [math-000S]
This is came from when I'm formalizing lemma 1.3.11 of Basic Category Theory, I miss a precondition ( below must be a natural transformation in the lemma) and try to prove an impossible thing.
Let be functors, and a family
Does must be natural?
Counterexample. [math-000T]
Counterexample. [math-000T]
The result is can be not natural.
This counterexample is given by Zhixuan Yang:
Let be the two-object one-arrow category, and be , and
where is the two elements set. For we choice and , then is not natural.
Definition. exterior algebra [math-000R]
Definition. exterior algebra [math-000R]
The exterior algebra of vector space is defined as a -graded algebra:
Definition. Homotopy extension property (HEP) [math-000O]
Definition. Homotopy extension property (HEP) [math-000O]
A map of spaces has the homotopy extension property for a space if
- for each homotopy
- and for each map with for all
there is a homotopy such that
for all , and . The idea can be expressed in the following commutative diagram:
The homotopy is called the extension of with initial condition .
Definition. Natural Transformation [math-000N]
Definition. Natural Transformation [math-000N]
Let and be categories, let be functors. A natural transformation is a function consists of
- For each , there is a morphism in , called the -component of
- For every morphism in , there is a commute diagram
常青筆記的困難 [note-0001]
常青筆記的困難 [note-0001]
Sterling 的 https://www.forester-notes.org/QHXX/index.xml 精確的描述了常青筆記可能遭遇的困難,關鍵在於,常青筆記對於不停變化的目標,如數學、電腦程式框架等存在,本體論的目標並不統一。用數學為例,我們傳統上接受 ZFC 作為「集合論」的本體,但 topos theory 的發展給出另一套定義 ETCS https://en.wikipedia.org/wiki/Elementary_Theory_of_the_Category_of_Sets!ETCS 說我們覺得集合論是「由 sets 與 functions 構成的 well-pointed topos,有自然數 object 與 Epics split」。
這個定義並沒有循環定義(但使用了短語簡化說法),因為 sets 跟 functions 的公理可以直接給出,ETCS 並沒有比 ZFC 不穩固。
事實上我們甚至知道 ETCS 跟 ZFC 的差異,ETCS + replacement(https://en.wikipedia.org/wiki/Axiom_schema_of_replacement)等價於 ZFC 的推理能力。ZFC 中的某部份等價於 ETCS(參考 Sheaves in Geometry and Logic: A First Introduction to Topos Theory VI. 10)
重點是,既然沒辦法保證討論主題的永久不變,那就應該紀錄當下對主題的洞見,因而在未來仍可從思想中復原出結構。
Definition. Pfaffian [math-000P]
Definition. Pfaffian [math-000P]
Let be a skew-symmetric endomorphism of a vector space (hence can also be view as a tensor: ) and is even, the Pfaffian of is the number defined as the constant factor in the tensor equality:
where is an orthonormal basis of .
The sign of Pfaffian depends on the orientation of the orthonormal basis.
An Agda Framework for Synthetic Mathematics [math-000K]
An Agda Framework for Synthetic Mathematics [math-000K]
https://samtoth.github.io/agda-synthetic-categories/index/index.xml
Theorem. Borsuk–Ulam [math-000L]
Theorem. Borsuk–Ulam [math-000L]
If is continuous then there exists a point such that .
Lemma. [math-000M]
Lemma. [math-000M]
If is continuous and antipode-preserving, then there exists a point such that .
Proof
Use standard stereographic projection, we can see and charts gives exactly the same coordinate system at equator (i.e. where its embedding coordinate with ). This also tells the equator is a in because .
By continuous and antipode-preserving, preserves such an equator (we denote ) to (with any deformation that still an antipode shape) and must bound a set contains .
By continuous, both of two open sets of , complement of , needs to be mapped to cover the subset of which bounded by , so there exists a point such that .
Proof
Define , is continuous.
By
is antipode-preserving.
By the lemma, there is a point such that , so then .
Determinant of Skew-Symmetric Matrices [math-000V]
Determinant of Skew-Symmetric Matrices [math-000V]
This problem arose from studying the book Lectures on the Geometry of Manifolds: Suppose is a real vector space, and is a symplectic duality, then has even dimension.
I can make some concrete computation on dimension 2 and 3 and roughly understand the reason, but I have no general proof.
After a month, I found a solution:
Proof. Using the properties of matrix column operations [math-000W]
Proof. Using the properties of matrix column operations [math-000W]
Since the multiplication factor of a matrix column can be extracted as a basis, flip the column 1 (i.e. the whole column multiply ) we have
Following this pattern, flipping column 2 gives us:
Let be an skew-symmetric matrix. After flipping all columns, we obtain , therefore
By definition, skew-symmetric means , so
When is odd, this gives us
Therefore must be 0.
After formalize this statement https://github.com/dannypsnl/blackboard/commit/2c0de90a98c24ae57bd30bc47ed8c3b6a75f2664, I found this need the field is charateristic 0, sure indeed satisfies that, this point to me is that Lean can help me refine my ideas.
If represents a duality, then . Therefore cannot be odd—it must be even.
What I Wish I Knew When Learning HoTT [tt-000P]
What I Wish I Knew When Learning HoTT [tt-000P]
Dependent Pattern Matching [ag-0001]
Dependent Pattern Matching [ag-0001]
{-# OPTIONS --safe --without-K #-} module ag-0001 where open import MLTT.Spartan
依賴類型有一些不同於常見語言的特徵,像是下面定義的這個類型
data So : 𝟚 → 𝓤₀ ̇ where oh : So ₁ ho : So ₀
在模式比對時 constructor oh 跟 ho
提供了變數 b 的訊息。
xxx : {b : 𝟚} → So b → 𝟚 xxx {b} oh = b -- 這裡 b 一定是 ₁ xxx {b} ho = b -- 這裡 b 一定是 ₀
Lecture. Domain Theory [dt-0000]
Lecture. Domain Theory [dt-0000]
Course. CS208 Logic & Algorithms [MSP-cs208]
Course. CS208 Logic & Algorithms [MSP-cs208]
Code and Materials for an interactive online course on Logic (part of Strathclyde's CS208 Logic and Algorithms module)
- project link: https://github.com/msp-strath/cs208-logic
- site link: https://personal.cis.strath.ac.uk/robert.atkey/cs208/index.html
Tool. agda 的開發工具 [agda-0001]
Tool. agda 的開發工具 [agda-0001]
我使用的編輯器工具是 Agda Mode on VS Code,也可以用 emacs 之類的。常用操作有
ctrl+c, ctrl+l 會編譯檢查檔案,假設程式中有
?,會被替換成所謂的 hole{! !},其實就是待寫的程式ctrl+c, ctrl+, 可以窺看 hole 的目標類型,與當前 context 有哪些 term 可用
ctrl+c, ctrl+r 會把 hole 中你打的程式碼往前提取,當然前提是類型是正確的
ctrl+c, ctrl+m 會把 hole 中你打的程式碼直接當成結果,一樣類型要是正確的
一般來說一個 agda 定義如下
hello : A → B hello a = {! !}ctrl+c, ctrl+c 會問你要把哪個變數用構造子分開,回答
a,假設有a1與a2兩個構造子,程式就會變成hello : A → B hello a1 = {! !} hello a2 = {! !}
使用 Linux 的使用者可以更改預設的 copy/cut 指令以免衝突。
已完成的軟體 [software-0007]
已完成的軟體 [software-0007]
已完成的軟體這種概念,是指一個軟體的功能已經沒有大幅度更動的必要,可以長期使用在產品上,而軟體本身只會進行必要的安全與移植性更新。我在 https://josem.co/the-beauty-of-finished-software/ 讀到這個想法。對應到筆記軟體上,我不希望軟體一直更新,尤其是當我一打開工具需要寫筆記時,上面的更新按鈕非常的讓人煩躁。同時,這個想法也是一種解放我們原先對軟體想像的開端,比起軟體如何如何,更重要的是真的去做,外部連結裡面也談到冰與火之歌正是用這樣的軟體寫出。
git send-email setup with Protonmail [software-0006]
git send-email setup with Protonmail [software-0006]
In the original setup I already explain the configuration, to do the same with Protonmail will need to install Proton Mail Bridge(https://proton.me/mail/bridge), then with configuration as below.
[sendemail] smtpEncryption = STARTTLS smtpServer = 127.0.0.1 smtpUser = <your id>@protonmail.com smtpServerPort = 1025 smtpPass = <your password>
Definition. point-surjective [math-000A]
Definition. point-surjective [math-000A]
A morphism is point-surjective iff for every point , there exists a point that lifts (satisfy ).
git send-email 的設定 [software-0004]
git send-email 的設定 [software-0004]
I use gmail, and hence, I need to get a Google app password. After having the password, one has to setup ~/.gitconfig with content:
[sendemail] smtpEncryption = tls smtpServer = smtp.gmail.com smtpUser = <your id>@gmail.com smtpServerPort = 587 smtpPass = <your password>
Then you are able to use git send-email command:
git switch -c branch-patch git format-patch main git send-email 0001-***********.patch
prompt will ask some questions, an important one is which mailing list is your target? After command success, your patch are sent.
For certain git repository you're working on, can config local repository via git config --edit, and add below to omit email list in command line.
[sendemail] to = <target email list>
Mastodon 私訊相比於一般通訊軟體 e.g. LINE, Telegram [software-0003]
Mastodon 私訊相比於一般通訊軟體 e.g. LINE, Telegram [software-0003]
好處
- 可以有效分類特定話題,例如一個串是講約去哪裡吃飯、另一個串講專業內容
- 可以用僅限提及的人,限制可見性,所以可以形成一定程度的群組概念
壞處
- 兩方站點的站長都能看到內容
- 客戶端不支援把一群提及名單固定成群組,這或許是一個可行的客戶端新功能
壞處的可能解法:公佈自己的 public key 讓對方加密訊息再傳,配上專用客戶軟體或許可以做的更方便
let Racket GC manage your FFI object [software-0005]
let Racket GC manage your FFI object [software-0005]
All you need are deallocator and allocator from ffi/unsafe/alloc.
(require ffi/unsafe
ffi/unsafe/define
ffi/unsafe/alloc)
(define-ffi-definer define-xxx
(ffi-lib "" '(#f)))
(define-xxx free-yyy (_fun _YyyRef -> _void)
#:c-id yyy_delete
#:wrap (deallocator))
(define-xxx make-yyy (_fun -> _YyyRef)
#:c-id yyy_new
#:wrap (allocator free-yyy)) Tool. ngrok [software-0002]
Tool. ngrok [software-0002]
Sometimes we didn't have public ip, but temporary wants to test website, ngrok can help in this situation.
# expose localhost:8080 by HTTP $ ngrok http 8080 # expose localhost:8080 by TCP $ ngrok tcp 8080
XDP [software-0001]
XDP [software-0001]
XDP is eXpress Data Path, it's a technology about putting a BPF code virtual machine on the NIC(network interface controller) driver before kernel network stack so that we can filter the packet before kernel, it would make processing speed greater.
We can do following things on the packet:
XDP_PASS: allow the packet to pass throughXDP_DROP: drop the packetXDP_TX: bounce the packet back on the same interfaceXDP_REDIRECT: redirects the packet to another interface
Here is an example of counting how many IPv4/6 packets be dropped.
package main
import (
"fmt"
"os"
"os/signal"
bpf "github.com/iovisor/gobpf/bcc"
)
// bcc is from iovisor/bcc this project
/*
#cgo CFLAGS: -I/usr/include/bcc/compat
#cgo LDFLAGS: -lbcc
#include
#include
void perf_reader_free(void *ptr);
*/
import "C"
const source string = `
#define KBUILD_MODNAME "foo"
#include
#include
#include
#include
#include
#include
#include
BPF_TABLE("array", int, long, dropcnt, 256);
static inline int parse_ipv4(void *data, u64 nh_off, void *data_end) {
struct iphdr *iph = data + nh_off;
if ((void*)&iph[1] > data_end)
return 0;
return iph->protocol;
}
static inline int parse_ipv6(void *data, u64 nh_off, void *data_end) {
struct ipv6hdr *ip6h = data + nh_off;
if ((void*)&ip6h[1] > data_end)
return 0;
return ip6h->nexthdr;
}
int xdp_prog1(struct xdp_md *ctx) {
void* data_end = (void*)(long)ctx->data_end;
void* data = (void*)(long)ctx->data;
struct ethhdr *eth = data;
uint64_t nh_off = sizeof(*eth);
if (data + nh_off > data_end)
return XDP_DROP;
uint16_t h_proto = eth->h_proto;
if (h_proto == htons(ETH_P_8021Q) || h_proto == htons(ETH_P_8021AD)) {
struct vlan_hdr *vhdr;
vhdr = data + nh_off;
nh_off += sizeof(struct vlan_hdr);
if (data + nh_off > data_end)
return XDP_DROP;
h_proto = vhdr->h_vlan_encapsulated_proto;
}
if (h_proto == htons(ETH_P_8021Q) || h_proto == htons(ETH_P_8021AD)) {
struct vlan_hdr *vhdr;
vhdr = data + nh_off;
nh_off += sizeof(struct vlan_hdr);
if (data + nh_off > data_end)
return XDP_DROP;
h_proto = vhdr->h_vlan_encapsulated_proto;
}
int index;
if (h_proto == htons(ETH_P_IP))
index = parse_ipv4(data, nh_off, data_end);
else if (h_proto == htons(ETH_P_IPV6))
index = parse_ipv6(data, nh_off, data_end);
else
index = 0;
long *value;
value = dropcnt.lookup(&index);
if (value) lock_xadd(value, 1);
return XDP_DROP;
}
`
func usage() {
fmt.Printf("Usage: %v \n", os.Args[0])
fmt.Printf("e.g.: %v eth0\n", os.Args[0])
os.Exit(1)
}
func main() {
if len(os.Args) != 2 {
usage()
}
module := bpf.NewModule(source, []string{
"-w",
})
defer module.Close()
fn, err := module.Load("xdp_prog1", C.BPF_PROG_TYPE_XDP, 1, 65536)
if err != nil {
fmt.Fprintf(os.Stderr, "Failed to load xdp prog: %v\n", err)
os.Exit(1)
}
device := os.Args[1]
if err := module.AttachXDP(device, fn); err != nil {
fmt.Fprintf(os.Stderr, "Failed to attach xdp prog: %v\n", err)
os.Exit(1)
}
defer func() {
if err := module.RemoveXDP(device); err != nil {
fmt.Fprintf(os.Stderr, "Failed to remove XDP from %s: %v\n", device, err)
}
}()
fmt.Println("Dropping packets, hit CTRL+C to stop")
sig := make(chan os.Signal, 1)
signal.Notify(sig, os.Interrupt, os.Kill)
dropcnt := bpf.NewTable(module.TableId("dropcnt"), module)
<-sig
fmt.Println("\n{IP protocol-number}: {total dropped pkts}")
for it := dropcnt.Iter(); it.Next(); {
key := bpf.GetHostByteOrder().Uint32(it.Key())
value := bpf.GetHostByteOrder().Uint64(it.Leaf())
if value > 0 {
fmt.Printf("%v: %v pkts\n", key, value)
}
}
} Algorithm. Mark sweep GC [cs-0008]
Algorithm. Mark sweep GC [cs-0008]
Mark-Sweep is a classic GC algorithm, it's combined with two parts, mark and sweep.
mark(root):
if not marked?(root):
mark(root)
for obj in knowns(root):
mark(obj)
sweep(heap):
for obj in heap:
if marked?(obj):
unmark(obj)
else:
release(obj)
If we run collection (mark-sweep), then since each object is reachable from root, so no one would be released.
After do some executions, obj1 don't need obj3 anymore, so it became:
Now when we run collection, obj3 is unreachable from root, so it won't be marked! When running to sweep, it will be dropped.