« Home

Simplex category 與 face maps [math-001I]

根據定義，每個 simplicial set SS 都是 simplex category Δ\Delta 的一個 presheaf

Definition. Simplex Category [local-0]

  1. Ob: 每個 object 都是 [n]:={0,…,n}[n] := \{0, \dots, n\} 並帶有整數的 order 結構（其中 nn 是非負整數）
  2. Hom: 每個 morphism 都是嚴格遞增函數 Δ([m],[n]):={ϕ:[m]→[n]∣x>y  ⟹  ϕ(x)>ϕ(y)}\Delta([m], [n]) := \{ \phi : [m] \to [n] \mid x > y \implies \phi(x) > \phi(y) \}

這些 morphism 可以用一類特殊的 maps 組出來，叫做 face maps，舉例來說

Broken pipe (os error 32)

這個定義乍一看實在沒辦法理解這在定義什麼，所以要實際看看幾個案例：從 [0][0] 到 [1][1] 可以畫成

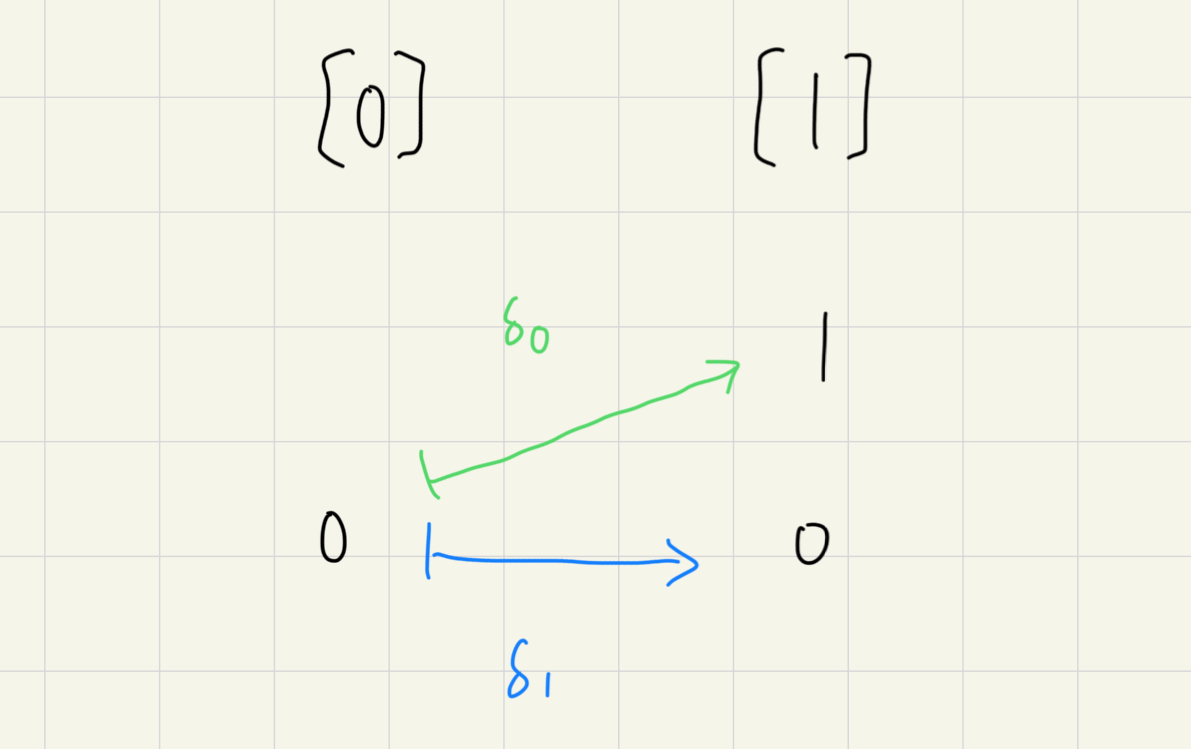
從 [1][1] 到 [2][2] 可以畫成

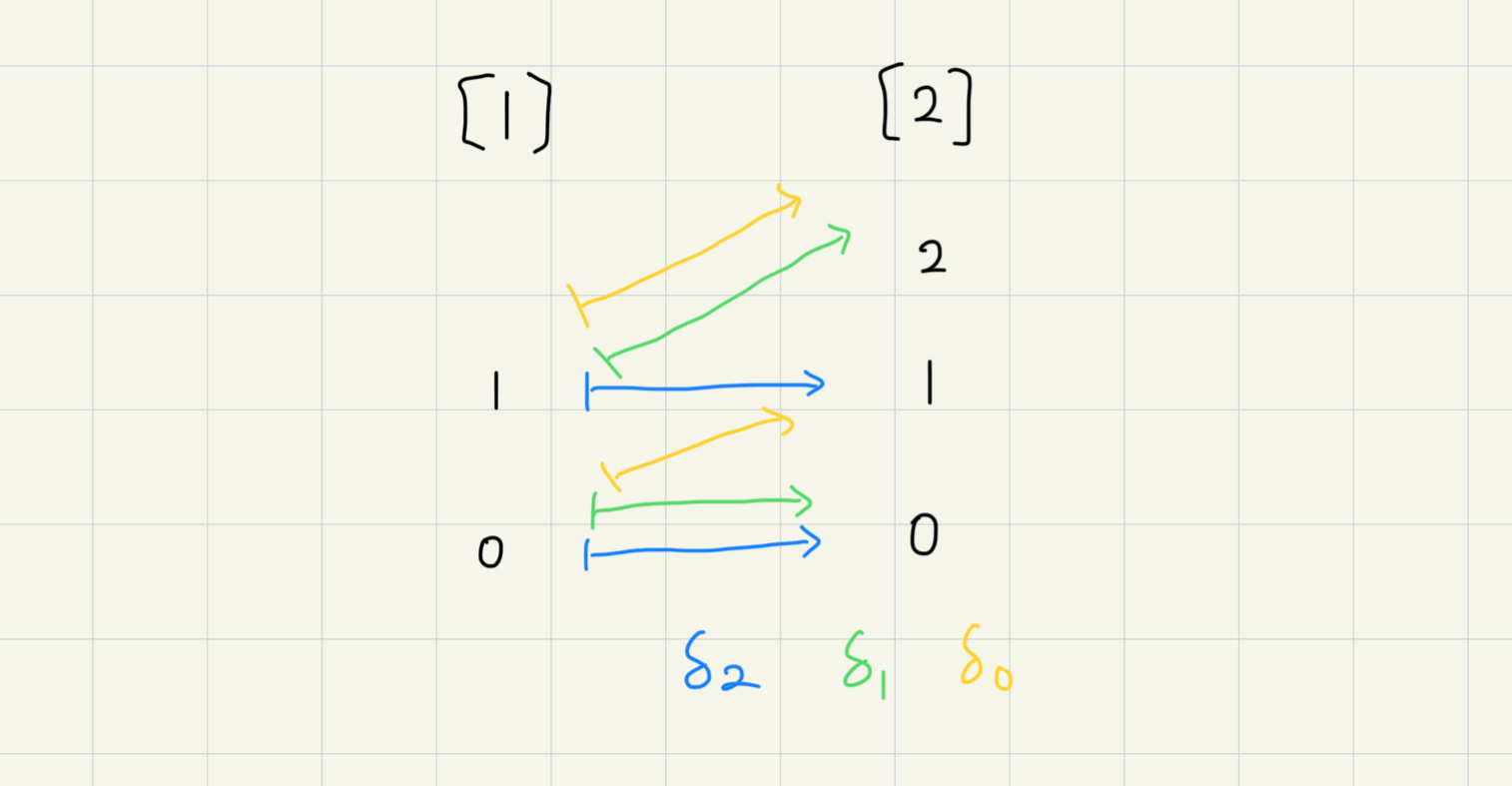
事實上，如果畫成 simplex 的幾何表示 Simpn\text{Simp}_n 就更明顯了：

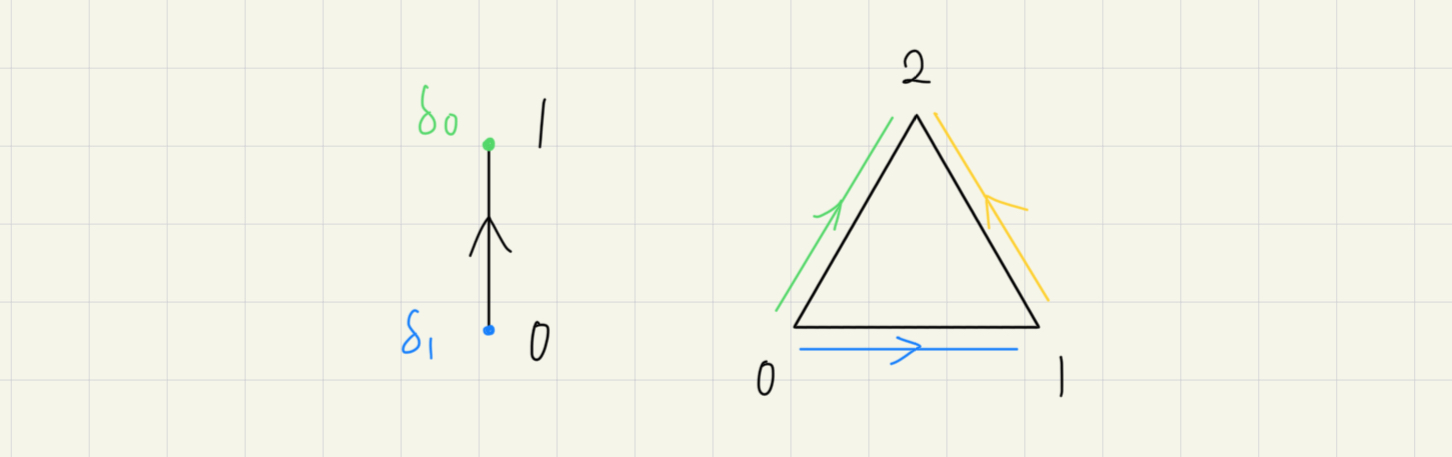
標準 nn-simplex Simpn\text{Simp}_n 可以定義成：

Simpn:={(x0,…,xn)∈[0,1]n∣∑ixi=1}\text{Simp}_n := \{ (x_0,\dots,x_n) \in [0,1]^n \mid \sum_i x_i = 1 \}

所以 face maps 就是在表示 [n−1][n-1] 表示 [n][n] 的哪一個邊界，線的邊界是兩個點，面的邊界是三條線。