具體的 simplicial set: Torus

simplex 要怎麼跟幾何扯上關係？這是因為 up to homotopy，我們可以把幾何形狀變形成用一群三角形（確切的來說是一些 simplex）表示的形狀。這裡要講的案例 Torus 是一個二維度的幾何曲面，一般定義成 $S^1 \times S^1$ 並畫成

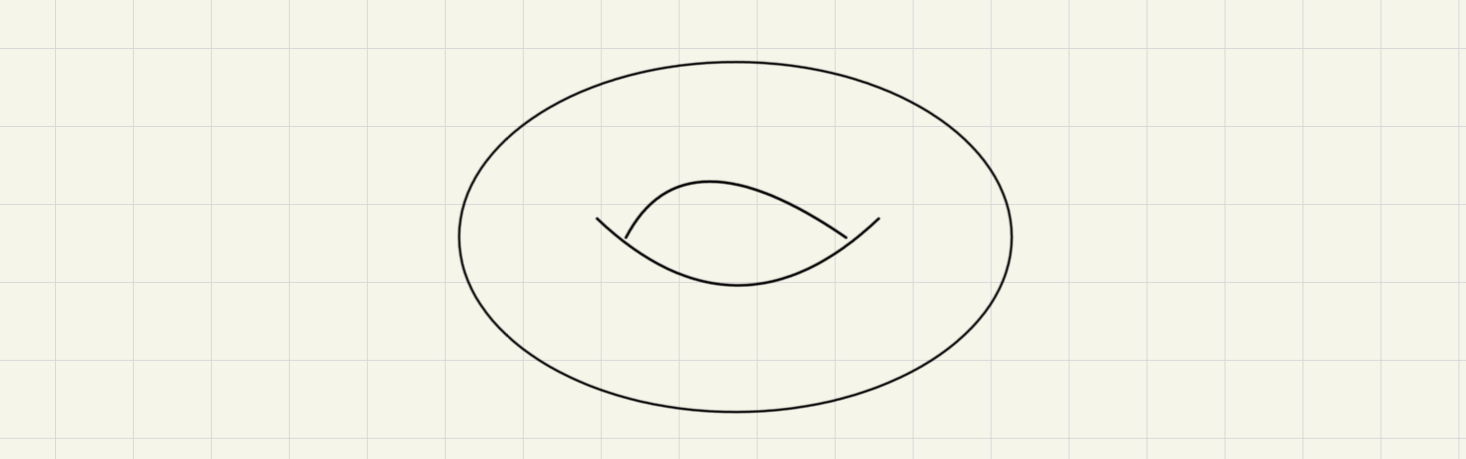
要怎麼三角化呢？通常會簡化成

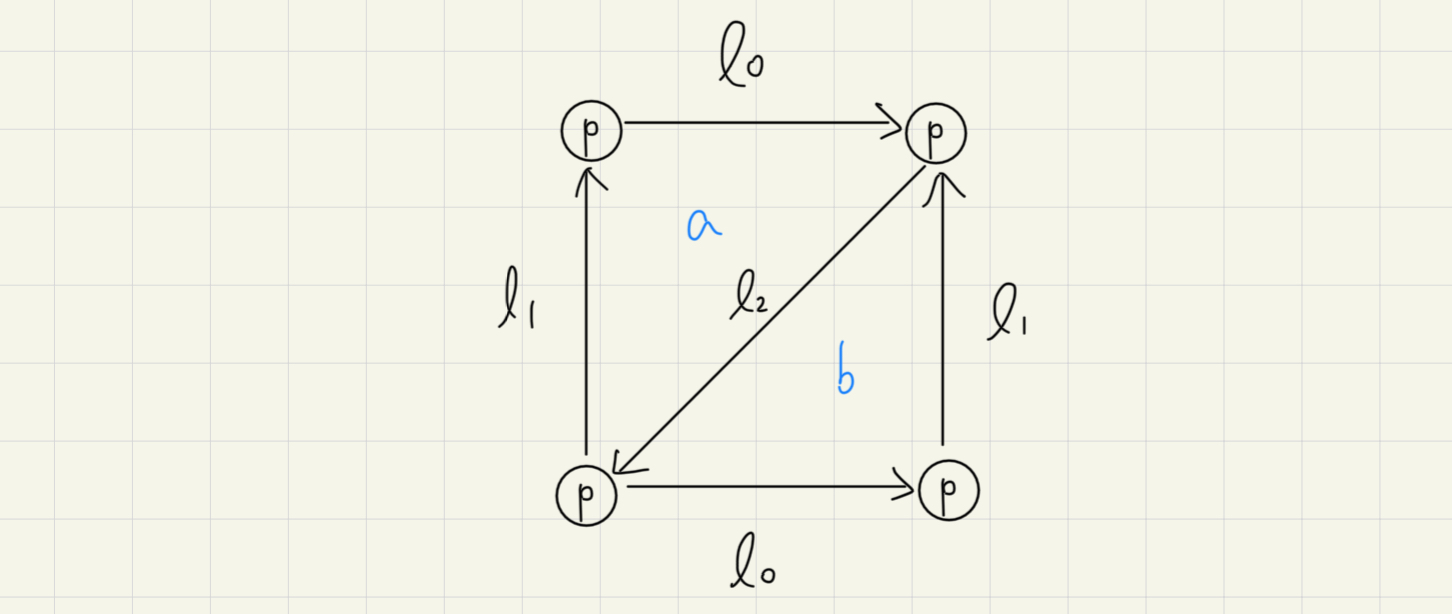
這怎麼變成幾何形狀的？注意到標為同一個名稱的那些線，那表示那其實是同一條線。這需要定義一個 simplicial set $\mathcal{S}$ （Hint: 根據定義是個 contravariant functor），其資訊如下：

\begin{aligned} \mathcal{S}[0] =\ &\{ p \} \\ \mathcal{S}[1] =\ &\{ l0, l1, l2 \} \\ \mathcal{S}[2] =\ &\{ a, b \} \\ \mathcal{S}\delta_i(l_j) =\ &p \\ \mathcal{S}\delta_i(a) =\ &l_i \\ \mathcal{S}\delta_i(b) =\ &l_{2-i} \\ \end{aligned}

視為其幾何實現（geometrical realization）：

|\mathcal{S}| := \big( \bigcup_i \mathcal{S}[i] \times \text{Simp}_i \big) / \sim

每個 topological space $\mathbb{X}$ 都導出一個 simplicial set $\mathcal{X}$ ，每個 $k$ -simplex 都是 $\text{Simp}_k$ 到 $\mathbb{X}$ 的連續函數：

\begin{aligned} \mathcal{X}[i] :=\ &\text{Hom}_{Top}(\text{Simp}_k, \mathbb{X}) \\ \mathcal{X}[\delta_i](f) :=\ &f \circ \delta_i \end{aligned}

每個連續函數，都給出了連續變形的過程；第二部分則是取 restriction，保持邊界關係。我下面展示如何逐漸變形來解釋其意義：

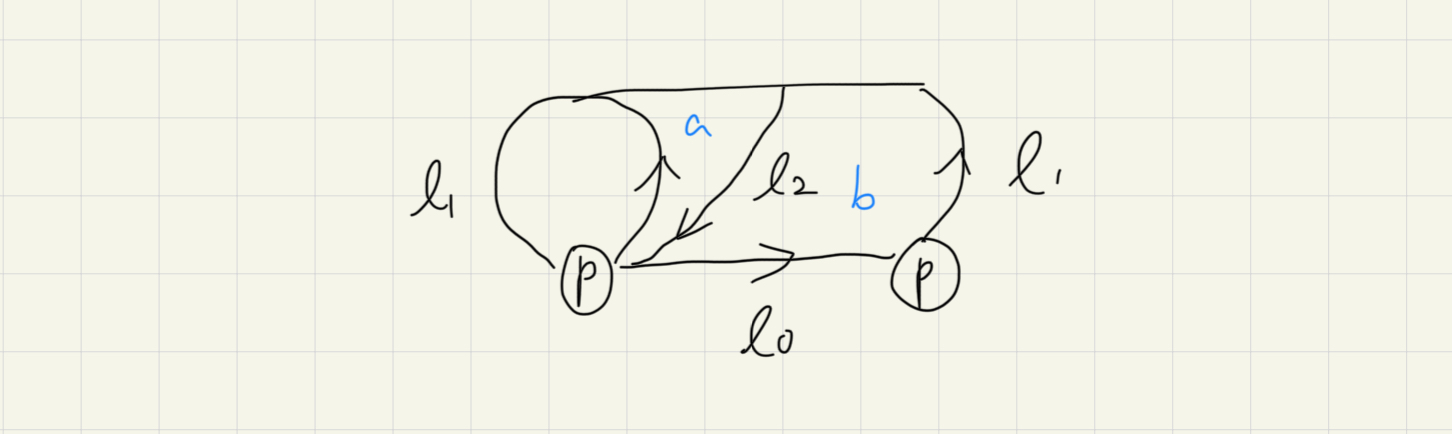
接著把管子對接

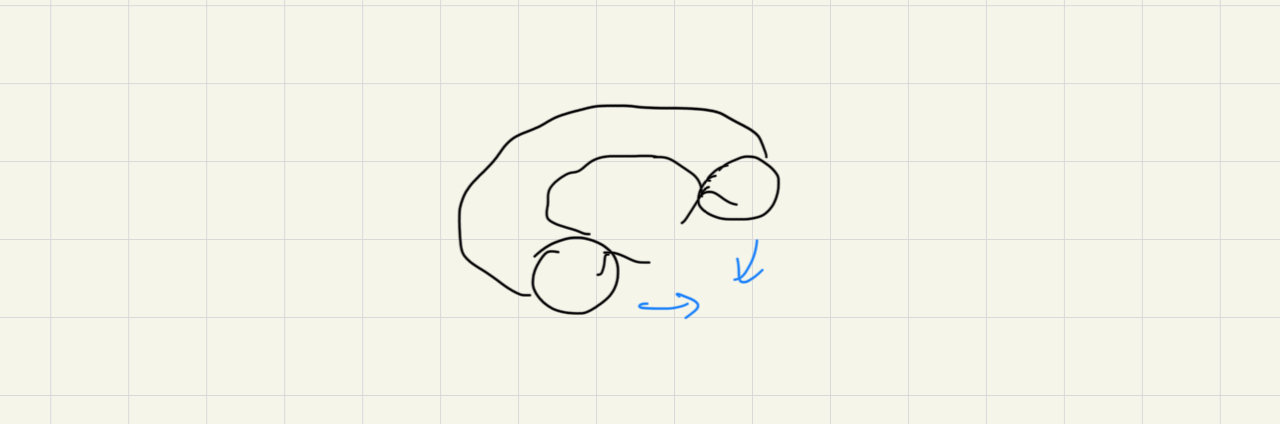
這確實是 Torus 的模型。